Area of Parallelogram and Triangles: Important Theorems

Parallelogram and Triangle are part of the basic geometric figures. Parallelogram is a polygon, which has 4 sides and it is also called a Quadrilateral. In a parallelogram, opposite sides are parallel to each other. Triangles on the other hand are geometric shapes with three sides. A triangle has vertex and interior angles. Based on the interior angles and sides of a triangle, it can be classified into many types.

Key Takeaways: Parallelogram, Triangles, Angle Sum property, Interior Angles theorem.

---

Parallelogram

[Click Here for Sample Questions]

Parallelogram is a two-dimensional geometrical shape. Parallelogram is a quadrilateral which has two pairs of parallel sides. The parallel sides are equal in length. Some important properties of a parallelogram are:

• Parallelogram is a 4 sided geometrical shape and hence has 4 vertices.
• In a parallelogram two opposite sides are parallel to each other and are congruent.
• Diagonals bisect each other in a parallelogram.

Parallelogram

To calculate the area of a parallelogram, Let us consider a parallelogram ABCD, where AB || DC.

Area of a parallelogram = Base × Height 

i.e Area of parallelogram ABCD = DC × BC

Read More:

---

Triangle

[Click Here for Sample Questions]

Triangle is a three-sided polygon. In a triangle, there are three edges, and three vertices. Based on the interior angles and sides of a triangle, it can be classified as follows:

• Equilateral Triangle

• Isosceles Triangle

• Scalene Triangle

• Right-angled triangle

There are three interior angles in a triangle. 

“The sum of the internal angles of a triangle is equal to 180 degrees”

This is one of the most important properties of a triangle also known as the angle sum property of a triangle. The area of a triangle is the region covered by the triangle in the 2D plane.

Also Read: Angle Sum Property of Quadrilateral

The formula for calculating the area of the triangle is as follows, Consider a triangle ABC

Triangle

Area of a Triangle= Half of Product of Base and Height

→ Area of Δ ABC = ½ × Base × Height

→ Area of Δ ABC= ½ × AB × BC

Also Read:

---

Important Theorems

[Click Here for Sample Questions]

Some of the important Theorems of Parallelogram and Triangle are as follows.

Theorem 1

Statement: Parallelograms on the same base and between the same parallels are equal in area.

Proof: Consider two parallelograms ABCD and EFCD with a common base DC and between the same parallel lines AF and DC. Here we need to prove that,

Area of parallelogram ABCD = Area of parallelogram EFCD

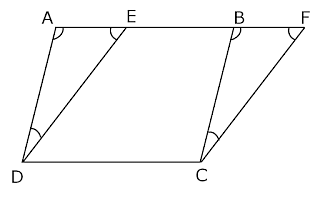
Now from the figure, In ΔADC and ΔBCF

∠DAE = ∠CBF (corresponding angles from AD ll BC)....(1)

∠AED = ∠BFC (corresponding angles from ED ll FC)....(2)

Therefore, ∠ADE = ∠BCF (Angle sum property of a triangle)....(3)

So ΔADC is congruent to ΔBCF (By ASA rule using equations 1,2,3)

Therefore, Area ADE = Area BCF (Because congruent figures have equal areas)....(4)

Now, Area ABCD = Area ADE + Area EDCB

Area ABCD = Area BCF + Area EDCB….from (4)

Area ABCD = Area EFCD

So parallelogram ABCD and EFCD with equal base DC are equal in Area.

Hence Proved

Also Read:

Theorem 2

Statement: Two Triangles on the same base (or equal bases) and between the same parallels are equal in area.

Proof: Let us suppose a parallelogram ABCD whose diagonal is AC. Let AN be perpendicular to DC.

We know that the triangle ADC is congruent to triangle ABC. Due to this area of the triangle, ADC is equal to the area of triangle ABC.

Therefore, Area of triangle ADC= 1/2 Area of parallelogram ABCD

Area of triangle ADC= 1/2 × DC × AN (AN is perpendicular to DC)

So, Area of  ΔADC= 1/2 × base DC × height AN 

Hence, Area of the triangle is half the product of its base and the corresponding altitude (height).

Also Read:

Theorem 3

Statement: Two triangles having the same base (or equal bases) and equal areas lie between the same parallels. 

Proof: It is given that triangle ABC and ABD are two triangles on the same base AB such that area of triangle ABC is equal to the area of triangle ABD.

We need to prove that CD II AB

It is clear from the diagram that CE ⊥ AB and DF⊥ AB (by construction)

therefore, CE II DF….(1)

Now, Area of triangle ABC = 1/2 × AB × CE

Area of triangle ABD = 1/2 × AB × DF

Since, Area of ΔABC = ΔABD (given)

Therefore, CF = DF….(2)

Now in CDFE,

CE II DF and CF = DF….from (1) and (2)

Hence, one pair of sides are parallel and equal. 

Therefore, CDFE is a parallelogram.

So, CD ll EF (Opposite sides of a parallelogram are parallel)

Therefore, CD ll AB

Hence Proved.

---

Things to Remember

• Parallelogram is a four sided polygon with four vertices. It can also be called a quadrilateral.
• Diagonals of a parallelogram bisect each other.
• Opposite sides of a parallelogram are equal and parallel to each other.
• Area of a Parallelogram = base × height.
• Triangle is a geometrical figure with three sides.
• There are several types of triangles such as right-angled triangle, equilateral triangle, Isosceles triangle etc.
• Area of a Triangle = 1/2 × base × height.
• Perimeter of a triangle = Sum of all sides.

Also Read: