
Collegedunia Team Content Curator
Content Curator
Algebraic expressions are the equations made up of constants, variables and arithmetic operators like addition, subtraction, multiplication and division by operating upon any variable. The numbers are determined by letters in algebraic equations and thus calculations are made easier. Most algebraic problems are simple phrases or descriptions of a math problem.
| Table of Contents |
Keyterms: Algebra, constants, variables, arithmetic operators, addition, subtraction, multiplication, division, algebraic expression
What are Algebraic Expressions?
[Click Here for Sample Questions]
An algebraic expression or a variable expression can be defined as a combination of the terms by arithmetic operations such as addition, subtraction, multiplication and division. For example, we can take a look at the expression 2x+5.
It can be said that the expression 2x+5 is an algebraic expression, since solving it can give us the answer we want. There are different components of an algebraic equation which are called constants, terms, variables and coefficients of an algebraic expression. The components are discussed below in greater depth.
Variables, Constants, Terms and Coefficients
A quantity whose value is not fixed, and it changes in the given subject or boundary of discussion is called a variable. Any arbitrary letter like x,y, z can be taken as a variable. These letters can take on the values of 1,2,3 or 4,5,6 or literally anything as long as we consider the math problem as the given boundary. Usually, in mathematica x,y,z are called variables though it can vary.
A symbol or a mathematical component which takes on a fixed value is known as a constant. All known numbers are constants. Any number like 6,-4 or 27.3 is a constant. In Mathematics, the letters p,q,r,s are usually used to determine constants but it can also vary.
A term can be a combination of variables or constants or a variable alone or a constant alone. A term can be expressed through multiplication or division operations. Some examples of terms are 5x^2, -(3y/4), (5+4x), etc.
The numbers which multiply or divide the variables in the above mathematical expressions are called coefficients. The numbers that are multiplying the expressions in the above paragraph are 5, -(¾) and 4. These numbers are called coefficients and they are important in understanding an equation’s value.

Variables, Constants, Terms and Coefficients
Terms of Algebraic Equations
[Click Here for Sample Questions]
A term in an algebraic equation can consist of just one constant, just one variable, product of both the variables or/and product of two or more variables. It can also consist of just the constant part. The terms can be either positive or negative. For example, 5x, 6xyz, 4x, 5y, -x, -y, 12xy, -12xy are all terms. It is already explained what coefficients are. In the term 4xyz, the coefficient is 4. In the case of the term yz, the coefficient is 1 and in the case of -8, the coefficient is simply -8.
In a polynomial equation, a degree is the highest integral power of the variable of its term when the polynomial is expressed in a standard form. If the term has multiple variables, degree can also be described as the sum of the exponents of all the variables in the term.
Formation of Algebraic Equations
[Click Here for Sample Questions]
An algebraic equation can have a single or multiple number of terms. If it contains just one term it might be the only constant term or one term consisting of variables and constants. It can be seen that the terms 8, 6y, -3yz, 6xy, 14 are algebraic expressions with just one term.
In cases where the algebraic term is formed as a result of multiple terms, they must be joined using an arithmetic operator like + or - sign. For example, 2x+4, -5x-y, 6xy+4x, are all such cases where symbols are required to show the union of multiple terms. Algebraic equations are thus formed and can be classified as having a single or multiple terms.
Types of Algebraic Expressions
[Click Here for Sample Questions]
Based on the number and types of variables found, values of exponents of the variables and the particular expression, different types of algebraic expressions can be derived. Based on the factors mentioned above, there are five different types of algebraic expressions. They are all summed up below.
- Monomial Expression- A monomial equation is the most simplistic kind of equation where there is only one term present and the exponents of all the variables are non-negative integers. For example, 4xy is a monomial expression.
- Binomial Expression- A binomial expression is an expression consisting of two monomial expressions. For example, (2/4)x-4xy is a binomial expression.
- Trinomial Expression- A trinomial expression is an expression consisting of three monomial expressions. For example, 4x-5y+z is a trinomial expression.
- Polynomial Expression- A polynomial expression can be defined as an expression consisting of one or more monomial expressions. For example, -2x+(4x^3+5)+3x+5 is a polynomial expression.
- Multinomial Expression- A multinomial expression can be defined as an expression consisting of one or more terms where the exponents of the variables can either be positive or negative. For example, 5x-2+3x+4y is a multinomial expression.
Algebraic Expressions Based on Variables
[Click Here for Sample Questions]
Algebraic equations can also be classified based on the number of variables it contains. The types are noted below.
- With one variable- If an algebraic expression has one variable only, like in the case of 4x, x-3, 4+x, y+6 etc
- With two variables- If an algebraic expression has two variables, like in the case of 3xy, 8x+4y, y2+5x, 4x2+8x-9y etc
- With three variables- In this case, the algebraic expression has 3 variables, like in the case of 3xyz, 6xy3+4y+z, z4-3x2+y etc.
Like and Unlike Terms
[Click Here for Sample Questions]
The terms having similar algebraic factors are known as like terms. The terms having dissimilar algebraic factors are known as unlike terms. We can take an example to demonstrate this further. In the expression 3xy-5x+6xy+3, the terms 3xy and 6xy are like terms because they have the same algebraic factors xy but the terms 3xy and 5x are unlike terms because they don't have the same algebraic factors. The algebraic factors of the two terms are xy and x respectively, which are dissimilar, which means they are unlike terms.
Arithmetic Operations on Algebraic Equations
[Click Here for Sample Questions]
The arithmetic operations based on algebraic equations are summarized below.
-
Algebraic Expression Addition
In the case of addition of algebraic expressions, the like terms can only be added to each other. Coefficients of like terms are added to get the desired result. Unlike terms do not undergo addition together and are left with whatever mathematical operator they have. One example can be noted to understand addition of algebraic expressions.
For the expression 2x+7y+z+4+3x+3y+6, the like terms can be written together. The expression then equates to 2x+3x+7y+3y+4+6+z. Z does not have a second term. The answer comes to 5x+10y+10+z, where the like terms are added and unlike terms are left alone with their respective mathematical operators.
-
Algebraic Expression Subtraction
For the subtraction of algebraic expressions, the signs change, like the + sign changes to - and the - sign changes to +, for the term which is to be subtracted from a given term. After that, the expressions go through the same rules as addition to give the expected result. An example is given to establish this better.
-
Algebraic Expression Multiplication
In case of multiplication of algebraic expressions, the product of two factors with similar signs are positive and the product of two factors with dissimilar signs are negative. In case of multiplication of two similar variables with different exponents, the powers of the variables are added.
-
Algebraic Expression Division
Divisions can be performed between algebraic expressions through algebraic identity and long division method. For example, in a division between x3-8 and x-2, x3-8 can be written as (x)3 – (2)3 = (x-2)[(x)2 + x.2 + (2)2]. The (x-2) on the numerator and denominator can be cancelled out and the result of the equation will be x2+2x+4. Here, the algebraic identity a3-b3= (a-b)(a2+ab+b2) is used. Long division method can be used in case of complex algebraic expressions. An example is given below.
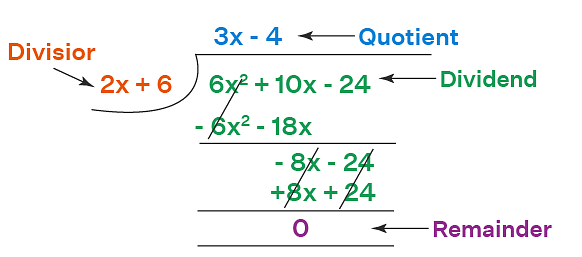
Long Division
Also Read:
| Related Articles | ||
|---|---|---|
| Geometric mean | Sequence and series | |
| Branches of Algebra | Sum of Squares | |
| Geometric Progression | Polynomials | |
| Permutations and Combinations | Arithmetic Progression | |
Things to remember
- The algebraic expression is defined as the combination of the constants and the variables connected by the fundamental operators of mathematics.
- In an algebraic equation, a term consists of constants and variables.
- A quantity whose value is not fixed is called a variable.
- A mathematical symbol which takes on a fixed value is known as a constant.
- A term in an algebraic equation can consist of just one constant, just one variable, product of both the variables or/and product of two or more variables.
- There are five types of algebraic terms; monomial, binomial, trinomial, polynomial and multinomial.
- Algebraic equations are used to shorten long problems into smaller parts which make problem solving easier.
Sample Questions
Ques. Add 5x2 – 7x + 3, – 8x2 + 2x – 5 and 7x2 – x – 2. (2 Marks)
Ans. The given problem is solved below.
=(5x2-7x+3)+(-8x2+2x-5)+(7x2-x-2)
= 5x2-8x2+7x2-7x+2x-x+3-5-2 (collecting like terms)
=(5-8+7)x2+(-7+2-1)x+(3-5-2) (adding like terms)
=4x2-6x-4.
Ques. Subtract (2x2-5x+7) from (3x2+4x-6). (2 Marks)
Ans. Here’s the solution:
=(3x2+4x-6)-(2x2-5x+7)
=3x2+4x-6-2x2+5x-7
=x2+9x-13.
Ques. Find the value of y when 5y+45=100. (3 Marks)
Ans. By isolating the variables from the constants, we get
5y= 100-45
Or, 5y= 55
By dividing both sides with the coefficient, we get
y=55/5
Or, y= 11.
Ques. Determine the value of the variable in the following equation: 2x+40=30. (3 Marks)
Ans. The variables should be separated from the constants which gives
2x = 30-40
2x = -10
Dividing both sides by 2,
We get x=-5.
Ques. Betty has m marbles. Annie has 5 more than 3 times the number of marbles Betty has. Which of these expressions denotes the total number of marbles that Betty and Annie have together? (3 Marks)
Ans. It is clear that the number of marbles Betty has is m.
3 times the number of marbles Betty has= 3m.
Annie has 5 more than 3 times the number of marbles Betty has. Therefore, Annie has 5+3m marbles.
The two of them together have (5+3m)+m number of marbles.
Therefore, the two of them together have a 5+4m number of marbles.
Ques. Multiply -5ab2c, 4a2b and -1/4. (2 Marks)
Ans. ={(-5)(4)(-1/4)} x {(ab2c)(a2b)}
={(-5)(4)(-1/4)} x {a.a.a.b.b.b.c}
={(-20)(-1/4)} x a3b3c
=5a3b3c.
Ques. Simplify the expression: 16m2-10m+6m-3m2-7m+12. (2 Marks)
Ans. Rearranging the terms, we get
=(16-3)m2+(-10+6-7)m+12
=(13)m2+(-11)m+12
=13m2-11m+12.
Ques. Sheila has x number of spoons in his kitchen. Lavanya has 4 times the number of spoons that Sheila has. Anand has double the number of spoons that Lavanya has. Which of the following expressions represents the number of spoons in Anand’s kitchen? (2 Marks)
1) 8x
2) 8+x
3) 2(x/4)
4) 16
Ans. Number of spoons Sheila has= x
Number of spoons Lavanya has= 4x
Number of spoons Anand has= 2.4x= 8x
Therefore, option 1 represents the number of spoons Anand has.
Ques. Sam fed his fish the same amount of food (let equal to x) thrice a day. How much food will he feed the fish in a week? (2 Marks)
Ans. Sam feeds his food x quantity of food, 3 times a day.
Therefore, he feeds his fish 3x quantity of food in a day.
In a week, he will feed his fish 3x.7 quantity of food.
Therefore, Sam will feed his fish 21x the amount of food per week.
Ques. The radius of circle A is r cm. The radius of circle B is twice the radius of circle A. What is the difference between the circumference of circle B and circle A (in cm)? (3 Marks)
Ans. Radius of circle A= r cm.
Radius of circle B= 2r cm.
Circumference of circle A= 2Πr cm.
Circumference of circle B= 2.2Πr cm= 4Πr cm.
Therefore, the difference between the circumference of circle A and circle A is= 4Πr cm- 2Πr cm= 2Πr cm.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments