
Collegedunia Team Content Curator
Content Curator
Closure property is where when a set of numbers undergo any mathematical operations then the result will be a number belonging to the same set of numbers. We use the closure property in addition, subtraction, multiplication and division of different types of numbers. For example, if we add two real numbers then the product will also be a real number.
What is Closure Property?
[Click Here for Sample Questions]
Closure property is where when a set of numbers undergo any mathematical operations then the result will be a number belonging to the same set of numbers. As we encounter a lot of different types of numbers ranging from natural, whole, rational, real numbers etc, we see that the closure property is associated with these different types of numbers. Or we can say that various operations of different types of numbers possess this property.
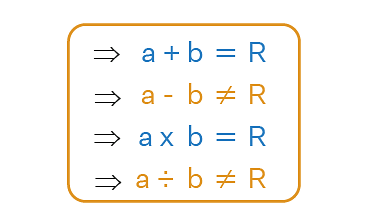
Closure Property
Let us consider the following examples.
Example 1: If we add two real numbers then the product will also be a real number.
5+4=9
4+2=6
Example 2: If we subtract the two whole numbers then we will get the whole number as a result.
4-0=4
7-5=2
Example 3: Any two whole numbers when multiplied gives the product of the whole number.
6×4=24
5×4=20
The table below shows the closure property of various numbers.
| Types of numbers | Addition | Subtraction | Multiplication | Division |
|---|---|---|---|---|
| Whole numbers | Closed | Not closed | Closed | Not closed |
| Integers | Closed | Closed | Closed | Not closed |
| Rational numbers | Closed | Closed | Closed | Not closed |
Also Read:
| Related Articles | ||
|---|---|---|
| Real numbers | Decimal expansion | Complex numbers and Quadratic equations |
| Geometric Mean (GM) | Rolle’s Theorem | Permutations and Combinations |
Closure Property of Whole Number
[Click Here for Sample Questions]
A set of whole numbers consists of a set of natural numbers along with zero.
We find that the whole numbers follow closure properties under different types of operations.
Addition
When the two whole numbers are added then their sum will also be a whole number.
5+4=9
4+2=6
2+3=5
3+3=6
As we see above when we add two whole numbers we get the result as the whole number.
Subtraction
When the two numbers are subtracted together then their result will also be the whole numbers.
7-5=2
5-4=1
3-2=1
7-2=5
We can see that when the two numbers are subtracted it also gives the whole number as a product.
Multiplication
When the two numbers are multiplied with each other then their product will also be whole numbers.
2×3=6
4×2=8
2×2=4
4×1=4
We can see that when both the numbers undergo multiplication then it gives the product as the whole number itself.
Division
Whole numbers sometimes follow and sometimes do not follow closure property under division.
15 ÷ 3 = 5 (whole number)
441 ÷21 = 21 (whole number)
33÷6 = 33/6 = 5.5 (not a whole number)
Thus the whole number does not follow the closure property under division.
Closure Property of Rational Numbers
[Click Here for Sample Questions]
Rational numbers also follow the closure property with different operations.
Addition
In the operation of adding two rational numbers, the sum obtained is also a rational number. Therefore we could say that a set of rational numbers is said to be closed under addition.
Thus it can be said that rational numbers are closed under addition.
Subtraction
Rational numbers under the subtraction operation are said to be closed.
3/7 - 4/6 = 46/42
2/9 - 3/2 = -23/18
Thus rational numbers are also closed under subtraction.
Multiplication
Rational numbers follow closure property under multiplication too.
In all the above results the sum is a rational number.
Division
If we divide any two rational numbers there is a probability that the result may or may not be a rational number. Therefore rational numbers are not closed under division.
-4/3 ÷2/6 = -4/1 (a rational number)
3/9÷5/4= 12/45 (a rational number)
20/8÷ 0/4 =10/0 (cannot be defined)
Thus rational numbers are said to be not closed under division.
Closure Property of Integers
[Click Here for Sample Questions]
Integers are a set of positive and negative numbers along with zero.
Addition
When adding two or more numbers from the set of integers the result we get is a number that also belongs to the set of integers.
23 + 45 = 68 (an integer)
-12 + 18 = +6 ( an integer)
-66 + -55 = -121( an integer)
Thus integers follow closure property under addition.
Subtraction
Integers are said to possess the closure property in subtraction. What we get as the difference after subtraction of two integers, is also an integer.
-15 - -76 = -61 (an integer)
+876 - -663 = +1539 (an integer)
Thus subtraction of integers is closed .
Multiplication
Integers possess the closure property in multiplication.
-56 × 2 = -112 ( an integer)
24 × -12 = -284 ( an integer)
-15 × - 25 = +375 (an integer)
Integers follow the closure property under multiplication.
Division
Division of two numbers belonging to the set of integers may not always get you the result as integers.
-15÷ -5 = 3 (an integer)
+56 ÷ - 8 = -7 (an integer)
-42 ÷ +10 = -42/+10 = -4.2 (not an integer)
Therefore integers could not be said to follow closure property under division.
Also Read:
| Related Articles | ||
|---|---|---|
| Sequence and Series | Arithmetic Progression | |
| Geometric Progression | Geometric Mean | |
| Straight Lines | Angle Between Two Lines | |
| Horizontal and Vertical Lines | Conic Sections | |
Things to Remember
- Closure Property is a mathematical operation that is used in addition, subtraction and multiplication of whole numbers.
- When the two whole numbers are added together then it will give the same result. That is, if we multiply two whole numbers together, we will get whole numbers as their product.
- Real numbers are the combination of two types of numbers i.e.rational and irrational numbers. It consists of positive integers, negative integers, fractional numbers and irrational numbers.
- Rational numbers are those numbers that are given in the form of p/q in which q is not equal to 0.
Sample Questions
Ques. What is the law of closure property? (2 marks)
Ans. The law of closure can be defined as, when an operation (such as adding, subtracting, multiplying etc) is performed on a number of sets like a real number, it always makes a member of the same result of a set.
Ques. What is the closure property of addition for Whole Number? (2 marks)
Ans. The closure property of addition can be more clear with the example. If we add two numbers that are a and b and their sum is equal to c, i.e. a + b = c, then c will always be a whole number. For any two whole numbers a and b, the sum is also a whole number.
Ques. Why is closure property important? (2 marks)
Ans. This property holds for subtraction and addition of whole numbers. The sum of any two whole numbers will forever be a whole number, for example if a and b are any two whole numbers, a + b will be a whole number.
Ques. Is closure property true for subtraction? (2 marks)
Ans. Since, the property of closure is true only for the case of subtraction, addition and multiplication but the integers division doesn't follow the closure property that means the quotient of any two integers a and b may not be an integer.
Ques. What is the whole number ? (2 marks)
Ans. The whole number can be defined as the number which doesn't include any fractional and decimal part. For example, 0, 1, 2, 3, 4, 5, 6, and 7 are all whole numbers.
Ques. What do you mean by rational number? (2 marks)
Ans. Rational number can be defined as the number which remains in the form of p/q in which p and q are the integer number and the value of q cannot be equal to zero.
Ques. Find an irrational number between √6 and 6. (2 marks)
Ans. Given √6 and 6,
A real number between √6 and 6 = ½ √6 + 1
But, 1 is a rational number and ½ √6 is an irrational number. The sum of a rational number and an irrational number always results in an irrational number.
So, ½ √6 + 1 is the irrational number that lies between √6 and 6.
Ques. What is the difference between rational and irrational numbers? (5 Marks)
Ans.
| S.No | Rational numbers | Irrational numbers |
|---|---|---|
| 1. | Rational numbers are those which can be expressed as a ratio of two numbers p and q where p and q are any integer and q is not equal to zero is called rational numbers. | Irrational numbers are those which cannot be expressed as a ratio of two numbers p and q where p and q are any integer and q is not equal to zero is called rational numbers. |
| 2. | These numbers are finite or recurring. | These numbers are non-repeating and non-recurring. |
| 3. | In this, both the numerator and denominator are integral values in which the denominator is equal to zero. | These numbers cannot be written in fractional form. So, there is no involvement of numerator and denominator. |
| 4. | Rational numbers include perfect squares such as 4, 9, 16, 25, 36 etc and so on. | Irrational numbers include surds instead of perfect squares such as √2, √6, √3, etc and so on. |
| 5. | Example - 3/2 = 1.5, 3.7676, 6, 9.31, 0.6666, etc and so on. | Example - √5, √11, e (Euler's number), π (pi), etc and so on. |
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Read:






Comments