
Collegedunia Team Content Curator
Content Curator
Hexagons, is a type of polygon polygon. A polygon is a closed chain of a finite number of line segments. The area bounded by these line segments is called a polygon. Polygons are 2-dimensional figures. Whereas a hexagon is a 6-sided polygon with six corners. The sum of internal angles of a hexagon is 720°. A hexagon having all its sides of the same length and equal vertex angles are called a Regular Hexagon.
| Table of Content |
Types of Hexagon
There are 4 different types of hexagon, based on the length of its sides and the angles. These types are as follows:
- Regular Hexagon: The hexagon having equal sides and angles is called a Regular Hexagon. The sums of the interior and exterior angles of a regular hexagon are 720° and 360° respectively.
- Irregular Hexagon: An irregular hexagon has unequal sides and angles. The sum of the interior angles of an irregular hexagon is still 720° but each angle does not measure 120°.
- Convex Hexagon: The hexagon having the interior angles measure less than 180° is a Convex Hexagon. It can either be regular or irregular, depending on the length of the sides and the angles.
- Concave Hexagon: The hexagon having at least one interior angle more than 180° is a Concave Hexagon. It is always an irregular hexagon.
Properties of Hexagon
Some of the important properties of the hexagon are as follows:
- A regular hexagon has 6 equal sides and 6 equal vertices.
- A regular hexagon has 9 diagonals.
- The sum of the interior angles of a regular hexagon is 720° and each interior angle is 120°.
- The sum of the exterior angles of a regular hexagon is 360° and each exterior angle is 60°.
- There are 6 axes of symmetry in a regular hexagon, with 3 of them passing through the diagonals and the other 3 passing through the midpoint of opposite sides.
- A regular hexagon can be divided into 6 equilateral triangles.
- The circumcircle (a circle that passes through all the vertices of a polygon) of the hexagon has its centre overlap with that of the hexagon and its diameter is the same as the diameter of the hexagon.
- The incircle (a circle that passes through the mid-points of the sides of a polygon) of the hexagon also has its centre overlap with that of the hexagon. The incircle is tangential to all the sides of the hexagon.
Also Read:
Formulas for the Perimeter and Area of Hexagon
For a regular hexagon, the formula for its perimeter is:
Perimeter = 6a
where
a = Length of a side
The formula for the area of a hexagon is:
Area = (3\(\sqrt{3}\)/2) a^2
where
a = Length of a side
Derivation of the Formula for the Area of Hexagon
Let’s have a hexagon with side “a” and divide it into 6 equal parts. This will give us 6 equilateral triangles.

To find the area of the hexagon, we will find the area of one equilateral triangle and multiply it by 6.
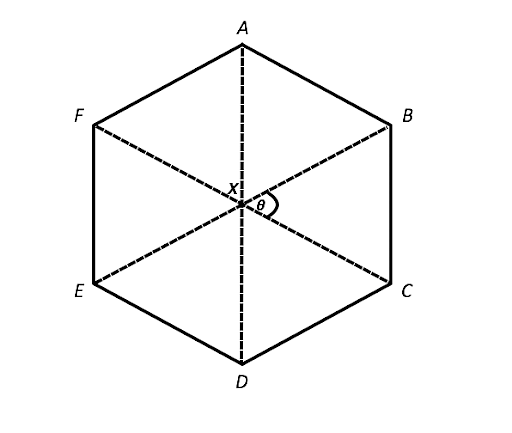
Let’s take the equilateral triangle BXC. Let the ∠BXC be θ. As there is a complete angle (360°) at X and each triangle is congruent, 360° will be divided into 6 equal angles.
Therefore, θ = 360° / 6 = 60°
Now, let’s drop a right-angle from X on the side BC. Let XY be h.
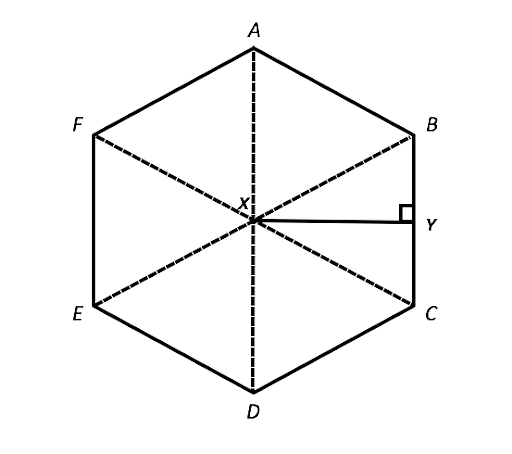
XY bisects the angle θ and the side BC. Therefore, ∠BXY = 30° and BY = a/2.
Now, we know that:
tanθ = Perpendicular / Base
tan(∠BXY) = BY / XY
tan(30°) = (a/2) / h
√3/3 = (a/2) / h
h = a/2 * 3/\(\sqrt{3}\)a
Now, the area of triangle BXC = ½ bh
Area = ½ x a x a/2 X 3/\(\sqrt{3}\)
Area = (3\(\sqrt{3}\)) (a^2)/4
As mentioned above, the area of hexagon = 6 x area of the triangle
Area of Hexagon = 6 x (3\(\sqrt{3}\)) (a^2)/4
Area of Hexagon = (3\(\sqrt{3}\)/2) a^2
Hexagon is a 6-sided polygon with six corners. The sum of internal angles of a hexagon is 720°
- A hexagon having all its sides of the same length and equal vertex angles are called a Regular Hexagon.
- An irregular hexagon has unequal sides and angles.
- The hexagon having the interior angles measure less than 180° is a Convex Hexagon.
- The hexagon having at least one interior angle more than 180° is a Concave Hexagon.
- Area of a Hexagon: 6 x (3\(\sqrt{3}\)) (a^2)/4
- The perimeter of a Hexagon: 6a
Also Read:
Sample Questions
Ques 1. Find the measure of interior angle if a regular polygon has 10 sides. (2 marks)
Ans. For a regular polygon of “n” sides, the measure of interior angle:
180 - {360/n}
For n = 10,
Interior angle = 180 - {360/10} = 144°
Ques 2. If the interior angle of a regular polygon is 80°, what regular polygon will we get? (3 marks)
Ans. Interior angle = 180 - {360/n}
80° = 180 - {360/n}
360/n = 180° - 80°
360/n = 100°
n = 3.6
Since “n” is not an integer, no such regular polygon is possible.
Ques 3. If a regular polygon has 14 diagonals, which polygon is it? (3 marks)
Ans. No. of diagonals of a regular polygon = n(n-3)/2
14 = n(n-3)/2
28 = n^2 - 3n
n^2 - 3n - 28 = 0
n^2 - 7n + 4n - 28 = 0
n(n - 7) + 4(n - 7) = 0
Therefore, n = 7, -4
Since the number of sides cannot be negative, n = 7. Hence, we have a regular heptagon.
Ques 4. Find the sum of exterior angles of a regular nonagon. (2 marks)
Ans. Number of sides of a nonagon = n = 9
Exterior angle = 360/n = 360/9 = 40°
Therefore, the sum of exterior angles = 40° x 9 = 360°
Ques 5. Find out the area and perimeter of a hexagon with the length of the side equal to 5cm. (2 marks)
Ans. a = 5cm
Area of Hexagon = (3\(\sqrt{3}\)/2) a^2 = (3\(\sqrt{3}\)/2) (5x5) = 75\(\sqrt{3}\)/2 sq. cm
Perimeter of Hexagon = 6a = 6 x 5 = 30 cm
Ques 6. If the area of a hexagon is 60\(\sqrt{3}\) sq. cm, find the length of its side and use it to find its perimeter. (3 marks)
Ans. Area of Hexagon = (3\(\sqrt{3}\)/2) a^2
60\(\sqrt{3}\) = (3\(\sqrt{3}\)/2) a^2
40 = a^2
a = 2\(\sqrt{10 }\) cm
Perimeter of Hexagon = 6a = 6 x 2\(\sqrt{10 }\) = 12\(\sqrt{10 }\) cm
Ques 7. If the perimeter of a hexagon is 42cm, find its area. (2 marks)
Ans. Perimeter of a hexagon = 6a
42 = 6a
a = 42/6 = 7cm
Area of Hexagon = (3\(\sqrt{3}\)/2) a^2 = (3\(\sqrt{3}\)/2) (7 x 7) = 127.305 sq. cm






Comments