
Content Strategy Manager
A rhombus is a special type of parallelogram having all sides equal in length. The main difference between a rhombus and a square is that a square's sides are bound by right angles while the internal angles of a rhombus might vary.
- The diagonals of a rhombus divide each other equally by bisecting at the midpoints and at right angles.
- Rhombus has the properties of both kites and parallelograms.
- The two pairs of opposite sides are congruent.
- Opposite angles in a rhombus are equal.
- The diagonals of a rhombus bisect each other at right angles.
- The area of a rhombus can be calculated using different formulas depending on the known parameters.
| Table of Content |
Key Terms: Area of Rhombus, Parallelogram, Midpoints, Perpendicular Bisector, Angles, Pythagoras Theorem, Kites, Rhombus, Square, Congruent angles, Straight line
Area of Rhombus
[Click Here for Sample Questions]
A rhombus is a type of parallelogram where opposite sides are parallel. The angles opposite to each other in a rhombus are equal, and the angles next to each other add up to make a straight line. The area of a rhombus is the area enclosed by the sides of the rhombus in a two-dimensional space.
- Parameters like base, height, diagonals, and trigonometry are used to find the area of a rhombus.
- It depicts the total number of unit squares that can fit into it.
- The unit used for the area of the rhombus includes cm2, m2, in2, etc.
The area of a rhombus can be found using different methods such as –
- Using base and height
- Using diagonals
- Using trigonometry
As per the figure below, the area shaded in yellow is considered the area of the rhombus.
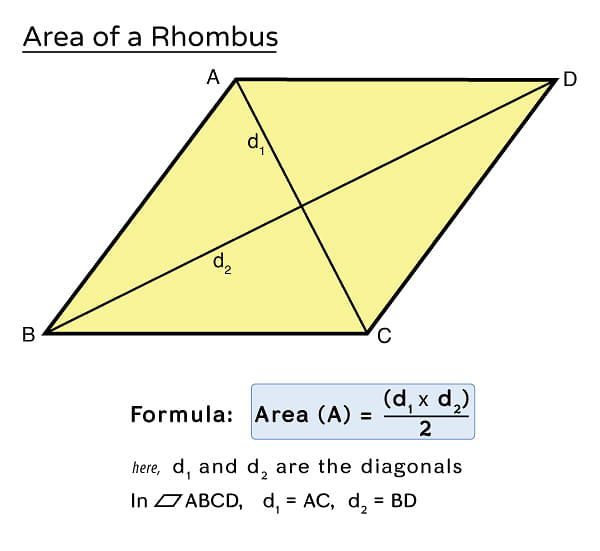
Area of Rhombus
Also Read:
| Related Articles | ||
|---|---|---|
| Perimeter of a Parallelogram | Area of Parallelogram and Triangles | Vector Formula |
| Difference Between Rhombus and Parallelogram | Trigonometry Values | Transversal and Angles |
Area of a Rhombus Formula
[Click Here for Sample Questions]
The formula for finding the area of a rhombus includes –
| Method | Formula |
|---|---|
| Base and Height | A = b × h |
| Diagonals | A = ½ × D × d |
| Base and Interior angle | A = b2 × Sin(a) |
Where:
- A is the area of the rhombus
- b is the base of the rhombus
- h is the height of the rhombus
- D is the length of the first diagonal
- d is the length of the second diagonal
- a is the interior angle of the rhombus
Area of Rhombus Using Base and Height
[Click Here for Sample Questions]
The area of a rhombus can be obtained simply by multiplying base and height parameters. The base is typically the horizontal side of the rhombus, and the height is the perpendicular distance from the base to the opposite side.
Apply the formula: Area = Base × Height

Solved ExampleExample: Consider a rhombus with a base of 10 centimetres and a height of 8 centimetres. Find the area of a rhombus. Solution: Using the formula, we have: A = 10 cm × 8 cm = 80 square centimeters Therefore, the area of the rhombus is 80 square centimetres. |
Read More:- Trigonometry Table
Area of Rhombus Using Diagonals
[Click Here for Sample Questions]
The diagonals of a rhombus are perpendicular bisectors of each other. Thus the area of a rhombus is equal to half of the product of the lengths of its diagonals.
Area of Rhombus Using Diagonals formula = (1/2) × d1 × d2
The resulting product represents the area of the rhombus in square units.

Area of Rhombus using Diagonals
In the given diagram, we have rhombus ABCD with diagonals AC and BD.
Considering that diagonal AC divides the rhombus into two triangles,
The area of rhombus ABCD can be expressed as the sum of the areas of triangles ADC and ABC:
Area of Rhombus ABCD = Area of ADC + Area of ABC
Since triangle ABC is congruent to triangle ADC, we can simplify the expression:
Area of Rhombus ABCD = 2 × Area of ABC
Now, let's calculate the area of triangle ABC:
Area of △ = ½ × Base × Height
The area of the rhombus (A) = 4 × area of ∆ AEB
= 4 x ½ x AE x EB
= 4 × (½) × (½) d1 × (½) d2 sq. units
= 4 × (1/8) d1 × d2 square units
= ½ × d1 × d2
Solved ExampleCalculate the area of a rhombus with diagonals of 6 centimeters and 8 centimeters. Solution: Using the formula, we have: A = (1/2) × 6 cm × 8 cm = 24 square centimeters Therefore, the area of the rhombus is 24 square centimetres. |
Read More:- Introduction to Trigonometry Revision Notes
Area of Rhombus using trigonometry
[Click Here for Sample Questions]
Calculating the area of a rhombus using trigonometry involves using the properties of triangles and sine functions. This method is particularly useful when you have the side length of the rhombus and one of its interior angles.
- Identify a side (a) and an interior angle (θ) of the rhombus.
- Recall the formula for the area of a triangle: Area = (1/2) × base × height.
- Express the base and height of the rhombus in terms of the side length (a) and angle (θ).
- Since the rhombus is symmetrical, the height (h) corresponds to half the length of a diagonal (d) divided by the sine of the angle (θ).
- Height (h) = (1/2) × diagonal (d) × sin(θ)
- Substitute the expressions for base (a) and height (h) into the triangle area formula:
- Area = (1/2) × a × [(1/2) × d × sin(θ)]
- Simplify the expression and obtain the final formula for the rhombus area using trigonometry:
- Area of Rhombus = 2 x (1/2) × a2 × sin(θ)
Area of Rhombus Using Trigonometry = a2 × sin(θ)
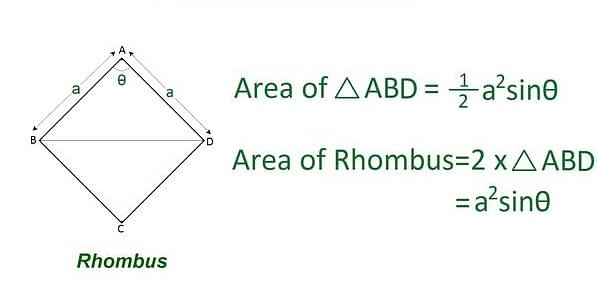
Area of Rhombus using Trigonometry
Solved ExampleExample: Calculate the area of a rhombus if the length of its side is 3 cm and one of its angles A is 60 degrees. Solution: Given, Side = s = 3 cm Angle A = 60 degrees Square of side = 3 × 3 = 9 Area, A = s2 × sin (60°) A = 9 × √3/2 A = 9 × 0.866 A ≈ 7.79 cm2 Therefore, the area of the rhombus is approximately 7.79 square centimeters. |
Things to Remember
- A rhombus is a special type of parallelogram with all sides equal in length.
- The area of a rhombus can be calculated using different formulas depending on the known parameters.
- The formula for calculating the area of a rhombus using base and height is Area = base × height
- The formula for area of a rhombus using diagonals is Area = (1/2) × d1 × d2, where d1 and d2 are the lengths of the diagonals
- Area of a rhombus using trigonometry can be calculated by the formula Area = a2 × sin(θ), where a is the side length and θ is an interior angle
- The area of a rhombus is measured in square units, such as cm2, m2, in2, and so on.
Also Read:
Sample Questions
Ques. Find the area of a rhombus having a side length of 7 inches and the height of the rhombus of 10 inches. (2 marks)
Ans. As we know, Area = base × height units2
Area = 7 × 10 inches2
Area = 70 inches2
The area of a rhombus with the given parameters is 70 inches2
Ques. The sides of a rhombus ABCD measure 5 cm, while the length of its one diagonal AC is 8 cm. Calculate its area. (4 marks)
Ans. The side and the diagonal lengths are given; thus we will find the other diagonal.
Let O be the point of intersection of diagonals.
All the sides of the rhombus are equal thus AB = BC = CD = AD = 5 cm
Area = (AC × BD)/2 sq. cm
AC = 8 cm
AO = 4 cm (∴ AO = 1/2 AC)
To find the other diagonal BD, consider AOD.
By Pythagorean theorem, AD2 = AO2 + OD2
52 = 42 + OD2
OD2 = 25 −16
OD2 = 9
OD = 3 cm
BD = 6 cm (?BD = 2 × OD)
Area = (8 × 6) ÷ 2 sq. cm
Area = 24 sq. cm
Area of the rhombus = 24 sq. cm
Ques. Calculate the area of a rhombus having diagonals equal to 9 cm and 12 cm. (3 marks)
Ans. Given that,
Diagonal 1, d1 = 9 cm
Diagonal 2, d2 = 12 cm
Area of a rhombus, A = (d1 × d2) / 2
= (9 × 12) / 2
= 108 / 2
= 54 cm2
Hence, the area of the rhombus is 54 cm2.
Ques. Find the diagonal of a rhombus if its area is 121 cm2 and the length measure of the longest diagonal is 22 cm. (3 marks)
Ans. Area of rhombus = 121 cm2 and let’s say d1 = 22 cm.
Using Area of the rhombus formula, A = (d1 x d2)/2 square units, we get
121 = (22 x d2)/2
121 = 11 x d2
d2 = 11
Therefore, the Length of another diagonal is 11 cm.
Ques. Logan has plans to raise a flower bed diagonally in his garden which is rhombus in shape. He measured and got the longest diagonal measured as 16 yards. He already knows the area of his garden to be 64 square yards. How long will the other flower bed be? (2 marks)
Ans. The area of the rhombus garden = 64 yards2 and let’s say the longest diagonal d1 is 16 yards.
Using Area of the rhombus formula, A = (d1 x d2)/2 square units, we get
64 = (16 x d2)/2
64 = 8 x d2
d2 = 8 yards
Therefore, the length of the other flower bed is 8 yards.
Ques. What is the area of a rhombus if the length of its side is 8 m and one of its angles A is 60º? (2 marks)
Ans. As we know, area of rhombus = s2 × sin(60º)
Area of rhombus = s2 × sin(60º)
= 82 × √3/2
= 64 × √3/2
= 32 √3 sq. m
Ques. Find the altitude of the rhombus whose area is 315 cm2 and its base is 45 cm. (2 marks)
Ans. Now, area of rhombus = b × h
315 = 45 × h
h = 315/45
h =7 cm
Therefore, the altitude of the rhombus is 7 cm.
Ques. The floor of the building consists of 4000 tiles rhombus-shaped and each of its diagonals is 40 cm and 25 cm in length. Find the total cost of polishing the floor if the cost per cm2 is Rs.5. (4 marks)
Ans. In each rhombus, the tile length of the diagonals = 40 cm and 25 cm
Therefore, the area of each tile-
A = (d1 x d2) /2
= (40 × 25) /2
= 1000/2
= 500 cm2
Therefore, the area of 4000 tiles = 4000 x 500
= 20,00,000 cm2
If per cm2 is Rs.5, thus 20,00,000 cm2 will be –
= 20,00,000 x 5
= 1,00,00,000
Thus it will take Rs. 1,00,00,000 to polish a floor of 4000 rhombus tiles.
Ques. What is the difference between calculating the area of a rhombus using base and height versus using diagonals? (3 marks)
Ans. The difference between calculating the area of a rhombus using base and height versus using diagonals lies in the information required.
- The base and height method requires knowing both the base length and the height, while the diagonal method only requires the lengths of both diagonals.
- In some cases, it may be easier to measure or obtain one set of parameters over the other.
Ques. Calculate the area of a rhombus with a side length of 5 centimeters and one of its interior angles measuring 60 degrees. (3 marks)
Ans. Method 1: Using Base and Height
Since the rhombus is symmetrical, we can divide it into two congruent triangles.
The base of each triangle is the side length (5 cm), and the height is half the length of a diagonal divided by the sine of the angle (θ).
In this case, the height is (1/2) × d × sin(60°), where d is the length of a diagonal.
The diagonal of a rhombus can be calculated using the Pythagorean theorem: d2 = s2 + s2, where s is the side length.
In this case, d2 = 52 + 52 = 50, so d = √50 ≈ 7.07 cm.
Therefore, the height is (1/2) × 7.07 cm × sin(60°) ≈ 3.85 cm.
Now we can apply the base and height formula: Area = base × height = 5 cm × 3.85 cm ≈ 19.25 cm2.
Method 2: Using Diagonals
The formula for calculating the area of a rhombus using diagonals is: Area = (1/2) × d1 × d2, where d1 and d2 are the lengths of the diagonals.
In this case, we already know that d ≈ 7.07 cm.
The other diagonal (d2) can also be calculated using the Pythagorean theorem: d2 = s2 + s2, where s is the side length. In this case, d2 = 52 + 52 = 50, so d2 = √50 ≈ 7.07 cm.
Therefore, the area is: Area = (1/2) × 7.07 cm × 7.07 cm ≈ 25 cm2.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Also Check:





Comments