Area of Rectangle: Formula and Sample Questions

Area of rectangle is the product of its length and breadth. It is the space enclosed by the rectangle in a 2-dimensional plane or the space occupied within the perimeter of the rectangle. A rectangle is a quadrilateral with 4 sides and 4 vertices. The opposite sides are parallel to each other. All the four angles of a rectangle are equal to 90^o. The length and breadth of the rectangle are however unequal. The area of rectangle is measured in square units.

Key Takeaways: Types of polygons, Rectangle, Area of Rectangle, Shapes, Geometry, Square, Diagonal

---

What is the Area of Rectangle?

[Click Here for Sample Questions]

A rectangle is a quadrilateral (polygon with four sides and four corners) with four right angles (of exactly 90 degrees). It can also be defined as a parallelogram with four right angles. Area of rectangle is the region occupied by a rectangle within its four sides. It is a two-dimensional property, thus it contains both length and breadth. 

Area of Rectangle Formula

The formula for the area of rectangle is the product of its length and breadth.

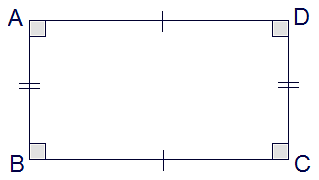
Let us take a rectangle with corners A, B, C, and D called ABCD

Area of rectangle = length × breadth

---

How to Calculate the Area of Rectangle?

[Click Here for Sample Questions]

To calculate the area of rectangle, you have to follow the steps below. 

1. Note the dimensions of length and breadth of the given rectangle.
2. Multiply length and breadth dimensions.
3. Write the area of rectangle i.e. the product of its length and breadth in square units. 

Also Read: Construction Formula

Example: Calculate the area of rectangle if it is 9m wide and 4m high.

Solution: l = 9m

b = 4m

Area of rectangle will be its length multiplied by its breadth

i.e. area of rectangle = l × b

Area = 9 × 4

Area = 36m²

---

How to Calculate Area of Rectangle Using its Diagonal?

[Click Here for Sample Questions]

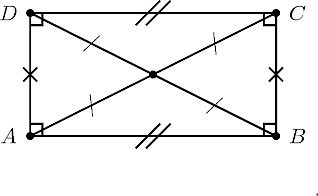
Diagonal of rectangle is the straight line connecting its opposite corners or vertices. There are two diagonals of equal lengths in a rectangle that can be calculated as: 

⇒ (Diagonal)² = (Length)² + (Breadth)²

⇒ (Length)² = (Diagonal)² - (Breadth)²

⇒ \(Length = (\sqrt{(Diagonal)^2 - (Breadth)^2})\)

The formula to calculate the area of rectangle is Length × Breadth.

Alternatively, we can write this product as

\(\sqrt{(Diagonal)^2 - (Length)^2} \times (Length)^2\)

Therefore, Area of Rectangle can also be written as:\(Breadth (\sqrt{(Diagonal)^2 - (Breadth)^2})\)

---

Why Area of Rectangle is Length into Breadth? 

[Click Here for Sample Questions]

The diagonals of a rectangle divide it into 2 equivalent right angled triangles. Therefore, the area of the rectangle is equal to the sum of the area of these two triangles.

Let us try to derive this formula of rectangle.

Suppose, ABCD is a rectangle.

Now, let diagonal AD divide rectangle into two right triangles, i.e. \(\bigtriangleup\)ABD and \(\bigtriangleup\)ACD.

We know that \(\bigtriangleup\)ABD and \(\bigtriangleup\)ACD are congruent triangles.

Area of \(\bigtriangleup\)ABD = ½ x base x height = ½ x AB x BC = ½ x b x l

Area of \(\bigtriangleup\)ACD = ½ x base x height = ½ x CD x AD = ½ x b x l

Area of rectangle ABCD = Area of \(\bigtriangleup\)ABD + Area of \(\bigtriangleup\)ACD

Area(ABCD) = 2(½ x b x l)

Area(ABCD) = l x b 

Thus, the area of rectangle = Length x Breadth

Read More:

---

Things to Remember 

[Click Here for Sample Questions]

• Area of rectangle = length x breadth
• A rectangle is a quadrilateral with four right angles of 90 degrees.
• Area of rectangle using a diagonal = \(Breadth (\sqrt{(Diagonal)^2 - (Breadth)^2})\)
• Area of rectangle is the space enclosed by the figure in the 2-D plane.

---