Muskan Shafi Education Content Expert
Education Content Expert
Pythagorean Triples are a set of three positive integers that satisfy the Pythagoras Theorem. According to the Pythagorean Theorem, the square of the hypotenuse (longest side) is equal to the sum of the squares of the other two sides of the right triangle.
Pythagorean triples are expressed as a2+b2 = c2 where a, b and c are the three positive integers. The Pythagorean triples are represented as (a,b,c) where, a is the perpendicular, b is the base and c is the hypotenuse of the right-angled triangle. (3,4,5) are the smallest and most known Pythagorean triplets.
What are Pythagorean Triples?
[Click Here for Sample Questions]
Pythagorean triples are sets of three numbers (usually integers) that satisfy Pythagoras' theorem. Pythagorean triples are made up of three integers (usually positive) where the square of the greatest of the three equals the sum of the squares of the other two. Pythagorean triples are expressed as a2+b2 = c2 where a, b and c represent the three positive integers.
Example: (3, 4, 5) is the most known and the smallest example of Pythagorean triples.
According to the Pythagorean triples formula, three positive numbers are called a Pythagorean triple if
a2+b2 = c2
Now, on evaluation,
32 + 42 = 52
9+16 = 25
Thus, 3,4 and 5 are a Pythagorean triple.

Pythagorean Triples Formula
[Click Here for Sample Questions]
The Pythagoras Theorem is a relationship between the squares on the sides of a right triangle. It states that the square of the hypotenuse (right triangle's longest side) is equal to the sum of the squares on the other two sides (the base and the perpendicular).
- The three alphabets (a, b, and c) that represent the three sides of a triangle are widely used to express the Pythagorean triples.
- The base and perpendicular are represented by ‘a' and ‘b,' respectively, while the hypotenuse is measured by ‘c.'
The Pythagorean triples formula states that it is a collection of three positive numbers such that:
\(c^2 = a^2 + b^2\)
The largest number among the three numbers in the given equation is ‘c.'
Read More: NCERT Solutions for Class 8 Maths
List of Pythagorean Triples
[Click Here for Sample Questions]
The list or set of the Pythagorean triples is endless. However, here is a list of some of the most common Pythagorean triples:
| (3, 4, 5) | (12, 35, 37) | (9, 40, 41) |
| (20, 21, 29) | (5, 12, 13) | (8, 15, 17) |
| (16, 63, 65) | (11, 60, 61) | (33, 56, 65) |
| (13, 84, 85) | (36, 77, 85) | (65, 72, 97) |
| (28, 45, 53) | (7, 24, 25) | (39, 80, 89) |
Read More: Class 10 Triangles
Pythagorean Triples Proof
[Click Here for Sample Questions]
In order to prove the Pythagorean Triples formula, let us take an example of a triplet (5, 12, 13).
Proof: Here, the hypotenuse (longest side of the right-angled triangle) is 13.
The other two sides are 5 and 12.
So, c = 13, a = 5 and b = 12.
According to the Pythagorean Triplet Formula, three positive numbers are called a Pythagorean triple if
\(c^2 = a^2 + b^2\)
132 = 52 + 122
169 = 25 + 144
169 = 169
Hence Proved.
Thus, we can verify or prove the Pythagorean Triples in this manner.
How to Form Pythagorean Triples?
[Click Here for Sample Questions]
We can form the Pythagorean triples in two cases. First when a given number is odd and second when the given number is even. Explained below is how we can form a Pythagorean triplet in both cases:
(I) When Number is Odd: If the given number is odd, the Pythagorean triplet will be (x, (x2/2 - 0.5) and (x2/2 + 0.5)).
For instance, consider 7.
The triples would be
- x = 7
- (x2/2) – 0.5 = (49/2) – 0.5 = 24.5 – 0.5 = 24
- (x2/2) + 0.5 = (49/2) + 0.5 = 24.5 + 0.5 = 25
Thus, the Pythagorean triple formed is (7, 24, 25).
(II) When Number is Even: If the given number is even, the Pythagorean triplet will be (x, (x/2)2-1, (x/2)2+1).
For instance, consider 16.
The triples would be
- x = 16
- (x/2)2 -1 = (16/2)2 – 1 = 82 – 1 = 64 – 1 = 63
- (x/2)2 +1 = (16/2)2 +1 = 82 + 1 = 64 + 1 = 65.
Hence, the Pythagorean triple thus formed is (16, 63, 65).
Read More: Even and Odd Numbers
Types of Pythagorean Triples
[Click Here for Sample Questions]
There are two types of Pythagorean triples: Primitive Pythagorean Triples and Non Primitive Pythagorean Triples.
Primitive Pythagorean Triples:
- A primitive Pythagorean triplet is a collection of three positive integers that satisfies Pythagoras' theorem if and only if all three numbers in the triples have no common divisor other than one.
- Only one even positive integer can be found in a primitive Pythagorean triplet.
- The Pythagorean triplet (3, 4, 5) is an example of a primitive Pythagorean triplet.
Non Primitive Pythagorean Triples:
- A non-primitive Pythagorean triplet is a group of three positive integers that follow the Pythagorean rule and share a divisor.
- There may or may not be more than one even positive integer in this triplet.
- 6, 8, 10 is an example of a non-basic Pythagorean triple.
Mathematics of Pythagorean Triples Formula
[Click Here for Sample Questions]
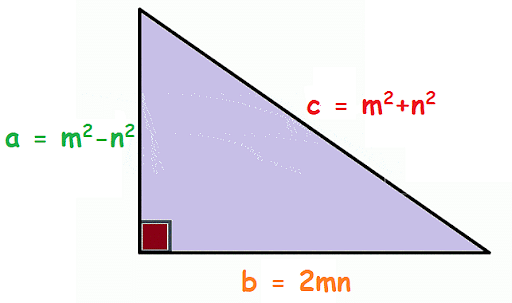
According to the Pythagoras theorem, if ‘a', ‘b', and ‘c' are the three sides of a right triangle, with ‘c' being the longest side, a2 + b2 = c2. The formula for determining the measure of ‘a', ‘b', and ‘c' can be calculated numerically as follows:
- a = m2-n2
- b = 2mn
- c = m2+n2
Note that m > n.
With these values, a right-angled triangle with sides a, b, and c is formed. The above-mentioned formulas can be used to find any number of Pythagorean triples by substituting the values of ‘m’ as any natural number.
Solved ExampleQues. Generate Pythagorean triples with the help of the two integers 2 and 3. Solution: As m > n m = 3 and n = 2. Substitute the values of m and n into the formulas of a, b, and c.
We can now check whether the values satisfy the Pythagorean theorem or not. According to the Pythagorean triplet formula: a2 + b2 = c2 52 + 122 = 132 25 +144 = 169 Hence Proved. Thus, we can say that (5, 12, 13) are Pythagorean triples. |
Generating Pythagorean Triples
Things to Remember
- Pythagorean triples are a set of three positive integers that satisfy the Pythagorean theorem.
- The Pythagorus triples formula is: \(c^2 = a^2 + b^2\)
- Three odd numbers can not form a Pythagorean triples formula.
- If a given number is odd, the Pythagorean triplet thus formed will be (x, (x2/2 - 0.5) and (x2/2 + 0.5)) .
- If a given number is even, the Pythagorean triplet thus formed will be (x, (x/2)2-1, (x/2)2+1).
- There are only two types of Pythagorean triples which include Primitive Pythagorean Triples and Non Primitive Pythagorean Triples.
Sample Questions
Ques. Make a Pythagorean triple out of the numbers 5 and 3. (3 Marks)
Ans. Let m = 5 and n = 2 since m must be greater than n (m > n).
a = m2 − n2
⇒a= (5)2 −(3)2 = 25−9 = 16
⇒ b = 2mn = 2 x 5 x 3 = 30
⇒ c = m2 + n2 = 32 + 52 = 9 + 25 = 34
Hence, (a, b, c) = (16, 30, 34).
Verifying the answer.
⇒ a2 + b2 = c2
⇒ 162 + 302 = 342
⇒ 256 + 900 = 1,156
1,156 = 1,156 (Hence Proved)
As a result, the triple (16, 30, 34) is a Pythagorean triple.
Ques. Check to see if the numbers (17, 59, 65) are a Pythagorean triple. (3 Marks)
Ans. Let, a = 17, b = 59, c = 65.
Test if, a2 + b2 = c2.
a2 + b2 ⇒ 172 + 592
⇒ 289 + 3481 = 3770
c2 = 652
= 4225
Because 3770 ≠ 4225, (17, 59, 65) isn't a Pythagorean triple.
Ques. Check to see if the numbers (7, 24, 25) are a Pythagorean triple. (3 Marks)
Ans. Pythagorean triple = (7, 24, 25)
a = 7, b = 24, c = 25
The Pythagorean triples formula is, c2 = a2 + b2
LHS: c2 = 252 = 625
RHS: a2 + b2 = 72 + 242 = 49 + 576 = 625
LHS = RHS
As a result, the number (7, 24, 25) is a Pythagorean triple.
Ques. Check to see if the numbers (5, 12, 13) are a Pythagorean triple. (3 Marks)
Ans. Given: a = 5; b = 12; c = 13
(The hypotenuse is the longest side; 13 is the longest side.)
We know that a Pythagorean triple satisfies Pythagoras' theorem using the Pythagorean triples formula: c2 = a2+b2
- H. S. = c2 = 132 = 169
- H. S. = a2 + b2 = 52 + 122 = 25 + 144 = 169
(5, 12, 13) is a Pythagorean triple because the given values meet the Pythagoras theorem.
Ques. Find the Pythagorean triplet with 18 as one of its components. (3 Marks)
Ans. Consider the Pythagorean triplet (a, b, c), which consists of:
a = m2 - 1, b = 2m and c = m2 + 1
Let us use the value of ‘b' of 18 as an example.
b = 2m
18 = 2m
m = 9
When we replace m = 9 in the calculations for a and c, we get,
a = m2 - 1 = 92 - 1 = 81 - 1 = 80
c = m2 + 1 = 92 + 1 = 81 + 1 = 82
As a result, the Pythagorean triplet (80, 18, 82).
Ques. Check whether 9, 12, and 15 are Pythagorean triples or not. (3 Marks)
Ans. According to the Pythagorean triplet formula,
c2 = a2 + b2
Here, a = 9, b = 12, c = 15
Substituting the values,
152 = 92 + 122
225 = 81 + 144
225 = 225
Thus, 9, 12 and 15 are Pythagorean triples.
Ques. What will be the other numbers of a set of Pythagoras Triples if one of them is 5? (3 Marks)
Ans. We can see that 5 is an odd number. Thus, if n is odd, the other Pythagorean triplet will be (x, (x2/2 - 0.5) and (x2/2 + 0.5)).
x = 5
(x2/2 - 0.5) = 25/2 - 0.5 = 12
(x2/2 + 0.5) = 25/2 + 0.5 = 13
Therefore, the Pythagorean triples thus formed are 5, 12, and 13.
Ques. Find out the other numbers of a set of Pythagoras Triples if one of them is 6. (3 Marks)
Ans. We can see that 6 is an even number. If n is even, the other Pythagorean triplet will be x, (x/2)2-1), (x/2)2+1).
x = 6
(x/2)2-1) = (6/2)2 -1 = 32 – 1 = 9-1 = 8
(x/2)2+1) = (6/2)2 +1 = 32 + 1 = 9 +1 = 10
Therefore, the Pythagorean triples thus formed are 6, 8, and 10.







Comments