
Collegedunia Team Content Curator
Content Curator
A linear equation can be defined as an equation between two variables, that when plotted on a graph, produces a straight line. It is an algebraic form of y = mx + b. Some of the properties of Linear equations are:
- It is like any other equation in which the product is directly proportional to the other plus the constant.
- The linear equation formula is also often called the equation of first order since it is an equation of a straight line.
- A linear equation is only known to have one or two variables.
- No variable in a linear equation can be raised to a power which is anything greater than 1 or used in the form of the denominator of a fraction.
Read also: Solving Linear Equations
| Table of Content |
Key Terms: Slope, x-intercept, y-intercept, Equation, Variables, Straight Lines
What is Linear Equation?
[Click Here for Sample Questions]
A linear Equation is an equation having the maximum order of 1 and an equation of a straight line. Simply, linear equation formula is also called the equation of first order because it is an equation of a straight line.
- It shows a relationship between unknown variables from the given data and is used to convert a statement into a mathematical statement.
- It is also known as the equation of first order as it is an equation of a straight line.
- By resolving the equation, one variable in it can be assessed.
- The product is equal to it which is also directly proportional to the other.
- The equation of a straight line is represented in various forms in coordinate geometry by extensively using this equation.
Read also: NCERT Solutions for Chapter 3 Pair of Linear Equations in Two Variables
Linear Equation Formula
[Click Here for Sample Questions]
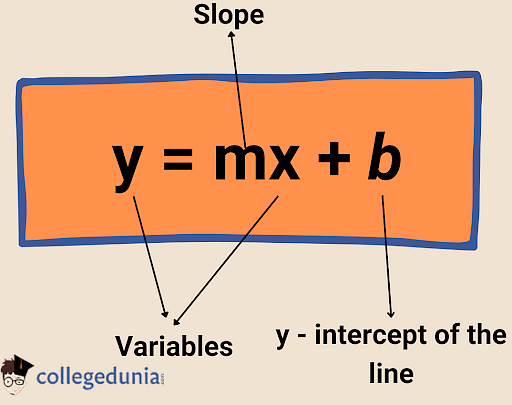
The term linear equation refers to an equation having a maximum order of 1 and an equation of a straight line. It is written in the form of a simple slope intercept which is:
| y = mx+b |
Where,
- m is the slope of the line
- b is the y-intercept
- x and y are the variables
Because (0,y) is the location where the line crosses the y-axis, the value of y when x is 0 is referred to as the y-intercept. Slopes provide information about a line's direction and steepness.
Linear Equation Formula
A linear equation can also be written in the following form:
| ax + b = 0 |
Where,
- x is a variable
- a and b are numbers
In coordinate geometry, this form is known as the Standard form of linear equation. It has to be noted that most linear equations do not start in this form. Thus, y=mx+c is called the straight-line equation in coordinate geometry.
Another form of straight line equation (y=mx=c) can be:
⇒ Ax + By + C = 0
∴ Here, A, B and C are constants.
Types of Linear Equations
[Click Here for Sample Questions]
The equation of a straight line with the y-intercept (0, 2) and the slope m = 4 is given by y = 4x + 2 on applying the linear equation formula (y = mx + b).
One-variable and two-variable linear equations can be represented in many forms where a line is defined in an (x, y) plane.
Some types of linear equation formula are tabulated below:
| Linear Equation Form | Formula | Explanation |
|---|---|---|
| Slope intercept form | y = mx + b | Where m is the slope of the line (known as gradient), b is the intercept, and a is a constant value. x and y are the points in the (x,y) plane. |
| General form | ax + by = c | Where a is not equal to 0, m is equal to – a/b and a,b and c are real numbers. |
| Two-Point form | y - y1 = m(x - x1) | Where x1 and y1 are points on the line m = y2 - y1/x2 - x1 and x1 is not equal to x2 |
| Vertical Line | x = p | p is the x-intercept. |
| Horizontal Line | y = q | q is the y-intercept. |
| Intercept form | x/x0 + y/y0 = 1 | Where x0 is x-intercept and y0 is y-intercept. |
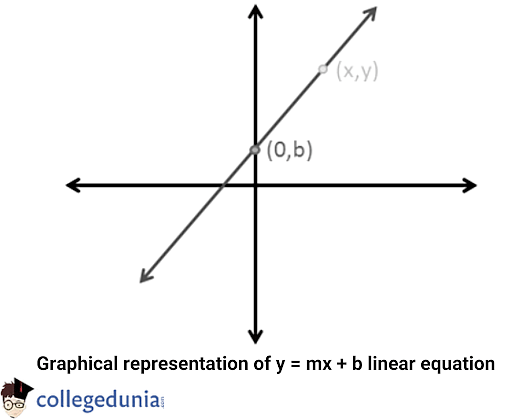
For a specific variable, its linear equation can be solved by using the substitution or elimination method or by the use of a graph. The graphical representation of the linear equation formula y = mx = b is as follows:
The graphical representation of the linear equation formula
Linear Equation Formula Derivation
[Click Here for Sample Questions]
According to the given figure,
- A slope with a line is one where the ratio of y-coordinate changes to x-coordinate change is equal.
- As the equation for slope intercept form is y=mx+b when the straight line and x-axis are in parallel, the x-coordinate will be equal to 0. Which states that y=b.
- When the straight line is parallel to the y-axis, the y-coordinate will be 0.
Therefore:
⇒ mx + b = 0
⇒ x = - b/m
The slope displays the ascent of the line in the plane, as well as the distance, travelled along the x-axis.
Read also:
Solving Linear Equations
[Click Here for Sample Questions]
The Steps to solve Linear Equations:
- If a=b then a+c=b+c. A number c can be added to both sides of the equation without changing the equation.
- If a=b then a-c=b-c. A number c can be subtracted from both sides of the equation without losing generality.
- If a=b then ac=bc. Both sides of the equation can be multiplied by a number c without affecting the equation.
- If a=b then a = ac = cb. Both sides of the equation can be divided by a non-zero number without losing generality.
Example of Linear EquationExample: Solve the following: (2x – 10)/2 = 3(x – 1) Ans. Step 1: First, clear the given fraction x – 5 = 3(x – 1) Step 2: Start simplifying on each side of the equation x – 5 = 3x – 3 x = 3x + 2 Step 3: Finally, Isolate x x – 3x = 2 -2x = 2 x = -1 |
Read also: Collinearity of Points
Things to Remember
- By using linear equation formula, we can represent the relationship between unknown variables from the given information.
- The linear equation formula can be expressed in an algebraic form, representing a simple-slope intercept, i.e. y = mx + b.
- The standard form of linear equation formula mainly contains the variable and a constant.
- The standard form of linear equation has the formula: ax + b = 0 (where a ≠ 0 and x is the variable).
Sample Questions
Ques. Find the value of y from the equation 2x + 4y = 20, where x = 24. (2 marks)
Ans. Put the value of x in the equation and solve for y,
Given x=24, 2x+4y=20
4y=20-2x24
4y=-28
y=-7.
Ques. Solve for x: 5x + 6 = 11. (2 marks)
Ans. Given function is 5x + 6 = 11
5x = 11 – 6
x = 5/5
x=1
Ques. Solve the given linear equation and determine the value of variable term x. 15 x – 55 = 20. (2 marks)
Ans. Given linear function is:
15 x – 55 = 20
i.e. 15 x = 20 + 55
i.e. 15 x = 75
i.e.x=75/15
i.e. x = 5
Ques. Solve the given linear equation and find the value of variable term x.
50 x + 60 = 110. (2 marks)
Ans. Given linear function is
50 x + 60 = 110
Dividing the equation by 10 both sides, we get
5x + 6 = 11
i.e. 5x = 11-6
i.e. 5x = 5
i.e.
x=5/5
i.e. x = 1
Ques. Solve the following systems of linear equations 3x – 2y = 4., – 3x + 5y = – 7. (2 marks)
Ans. The first equation, 3x – 2y = 4 (1)
and
Second equation,-3x + 5y = -7 (2)
Now add equation 2 to equation 1
3x−2y+(−3x+5y)=4+(−7)
3y = -3
y = -1.
And putting the value of y in any one of these two equations
We get,
3x + 2 = 4
x=⅔.
Ques. Solve the following systems of linear equations
3x + y + 1 = 0
2x – 3y + 8 = 0 (2 marks)
Ans. 3x + y + 1 = 0 (1)
2x – 3y + 8 = 0 (2)
Substitute x = 0 in equation (1), we get,
3(0)+y+1=0
y+1=0
y=−1
So, we get x = 0 and y = – 1.
Substitute y = 0 in equation (1),
3x+(0)+1=0
3x+1=0
3x=−1
x=−1/3
Ques. Romila went to a stationery shop and purchased 2 pencils and 3 erasers
for 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and
she also bought 4 pencils and 6 erasers of the same kind for 18. Represent this
situation algebraically. (2 marks)
Ans. Let us denote the cost of 1 pencil by x and one eraser by y. Then the
algebraic representation can be given as follows -
2x + 3y = 9
4x + 6y = 18
Ques. Akhila goes to a fair with 20 and wants to have rides on the Giant Wheel and play Hoopla. Represent this situation algebraically. (2 marks)
Ans. The pair of equations formed -
y = 1/2 x
i.e., x – 2y = 0
3x + 4y = 20
Ques. Govind gets the equation of a straight line 3x + 4y = 15. Help him find the slope. (3 marks)
Ans. Given 3x + 4y = 15
This equation is of the general form: ax+by = c
In the equation 3x + 4y = 15, a = 3 and b = 4
Using the linear equation formula, we get the slope as m = -a/b
m = -3/4
Thus the slope of this straight line is m = -¾.
Ques. Rohan’s piggy bank has 11 coins (only quarters or dimes) that have a value of $1.85. How many dimes and quarters does the piggy bank has? (5 marks)
Ans. Let's assume that,
Number of quarters = x
Number of dimes = y
As there are 11 coins, x=y=11 — (1)
y=11-x
Total value of money in the piggy bank is $1.85
100 cents =$1, 1 quarter=$1, 10 dimes=$1
Therefore we get, 10x+25y=185 — (2)
Solve (1) and (2) using substitution,
10x+25(11-x)=185
15x+275=185
-15x=-90
x=6
Substitute x value in (1)
y=11-6
y=5
Also check:






Comments