
Collegedunia Team Content Curator
Content Curator
Equation system consists of two equations also known as a pair of linear equations. They together make a system of equations. Every pair of equations has its own solution. Based on the type of solution, their type of system is decided. Finite, infinite and no solution are the types of solutions. Based on them, a pair of linear equations or the system of equations is labelled as a consistent and inconsistent system.
Read More: pair of linear equations in two variable
| Table of Content |
Key Terms: Linear equations, linear equations in two variables, system of equations, consistent system, real numbers, inconsistent system, graph
Consistent System
[Click Here for Sample Questions]
When the linear pair of two equations have one solution, share at least one solution, they belong to the consistent system. This system can be further classified based on the number of solutions a pair of equations can have. The solutions of a pair of linear equations can be easily derived by using a graph. A pair of equations can be represented as –
a1 x + b1 y + c1 = 0 and a1 x + b1 y + c1 = 0
Examples -
-7x + 2y + 3 = 0 and 5x = y
Here,
a1 = -7
b1 = 2
c1 = 3
a2 = 5
b2 = -1
c2 = 0
2x + 3y – 7 = 0 and 9x – 2y + 8 = 0
Here,
a1 = 2
b1 = 3
c1 = -7
a2 = 9
b2 = -2
c2 = 8
As per the three variables a, b, c, in a consistent system all the three variables should either have parallel planes or any two variables should be parallel while the third plane should meet these two planes at some point.
Read More: Applications of Determinants and Matrices
Independent System
When a pair of equations in a consistent system have exactly one solution (unique solution) satisfying both the equations it belongs to an independent system. They are also known as Linear Independence.
Here,\(\frac{a1} {a2}\) ≠ \(\frac{b1} {b2}\)
While representing both the equations in a graph, the solution lines intersect each other. For example, x – 2y = 0, 3x + 4y – 20 = 0 can be represented on the graph as follows,

Intersection of Solution lines
Here the point Q is the point where both the lines intersect. Thus point Q with x as 4 and y as 2 becomes one common solution for both the equations.
Dependent System
When a pair of equations in a consistent system has more than one solution (infinite solutions) satisfying both the equations it belongs to a dependent system. They are also known as Linear Dependence.
Here,
While representing both the equations in a graph, the solution lines are coincident to each other. Since each and every point on one solution line overlaps every point on the solution line of the other equation, we have infinitely many solutions for those pairs of equations.
For example, y = 2x +1, -4x + 2y = 2

The red solution line belongs to y = 2x + 1 and the blue line belongs to -4x + 2y = 2.
Discover about the Chapter video:
Determinants Detailed Video Explanation:
Inconsistent System
[Click Here for Sample Questions]
In an inconsistent system, the pair of equations given do not have any solution in common.
Here, \(\frac{a1} {a2}\) ≠ \(\frac{b1} {b2}\) ≠ \(\frac{c1} {c2}\)
While representing them graphically, we see the solution line of both the equations to be parallel to each other. Parallel lines never intersect each other; thus they do not have a common solution. For example, y = 5x + 4, 10x – 2y = 4
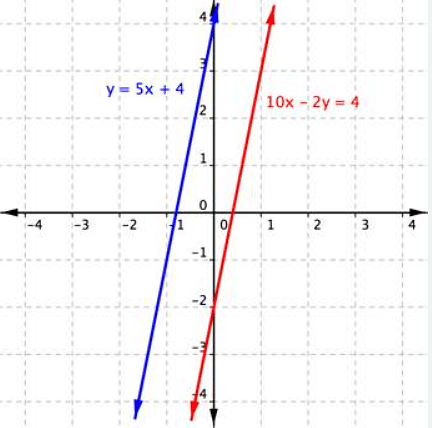
System of Equations
[Click Here for Sample Questions]
System of equations is tabulated below.
| Algebraic Representation | ||
|---|---|---|
| Consistent System | Inconsistent System | |
| Independent | Dependent | |
| \(\frac{a1} {a2}\) ≠ \(\frac{b1} {b2}\) | \(\frac{a1} {a2}\) =\(\frac{b1} {b2}\)= \(\frac{c1} {c2}\) | \(\frac{a1} {a2}\) = \(\frac{b1} {b2}\)≠ \(\frac{c1} {c2}\) |
Things to Remember
- Different systems of the equations can be represented graphically as well as algebraically.
- Without solving an equation graphically, just by looking at it, we can conclude the system of the equation using algebraic conditions.
- The linear equations of ax + b y + c = 0 type have a, b, c as real numbers.
- The values of x, y is the solution of the equation and based on these solutions, the pair of linear equations are classified into different systems.
- The linear equations with three variables can also be represented on the graph.
- We can also use the elimination method where we eliminate one variable by equating it in both the equations. After equating one variable, we add or subtract both the equations to get the value of the other variable. Using this value and substituting it in any one-off both equations, we can get the value of the previously eliminated variable
Read More: Geometric Progression (G. P.)
Sample Questions
Ques. The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement. (2 Marks)
Ans. Let the cost of the notebook be Rs x
And the cost of the pen be Rs y
As per the condition given in the question,
Cost of the notebook = 2 × Cost of the pen
x = 2y
x – 2y = 0 is the linear equation in two variables to represent the given statement.
Ques. Which one of the following options is true, and why? y = 3x + 5 has (3 Marks)
a unique solution,
only two solutions,
infinitely many solutions
Ans. y = 3x + 5 can also be written as – 3x + y – 5 = 0. This equation is a linear equation in two variables as it is in the form of ax + by + c = 0. Substituting different values for x, we can see that,
| y = 3x + 5 | ||
|---|---|---|
| x | y | (x, y) |
| 0 | 5 | (0, 5) |
| 1 | 8 | (1, 8) |
| 2 | 11 | (2, 11) |
As seen above we can get many numbers of solutions for whichever values we substitute, thus y = 3x + 5 has an infinite number of solutions.
Ques. Give the equations of two lines passing through (2, 14). How many more such lines are there, and why? (3 Marks)
Ans. Here we need to find linear equations which have solutions as (2, 14). Let’s take (2, 14) as (x, y). Simply add them to get the first equation, x + y = 16 (because 2 + 14 = 16). Now subtract them x – y = -12 (because 2 – 14 = - 12). We know that 2 × 7 = 14; thus, we can make another equation 7x = y (because 7 × 2 = 14), that equation can also be written as 7x – y = 0. In this way there can be a number of lines which can have their solution as (2, 14). Thus, we can conclude that the equations of two lines passing through (2, 14) are infinite.
Ques. Solve (3 Marks)
2x − y = 4
6x − 3y = 12
Ans. Let’s consider,
2x − y = 4 … (1)
6x − 3y = 12 … (2)
For equating eqn (1) to eqn (2) multiplying eqn (1) with 3 we get,
6x – 3y = 12 … (3)
Eqn (2) and eqn (3) are same equations, subtracting them will give the answer as ‘0’
The equations (2), (3) follow the inconsistent system where,
\(\frac{a1} {a2}\) = \(\frac{b1} {b2}\)≠ \(\frac{c1} {c2}\)
Thus, these equations will not have any solutions, they plot parallel lines when plotted in a graph. Thus, they will have no solutions.
Ques. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b, and c in each case: (5 Marks)
2x+3y=9
x- y/5-10=0
x=3y
2x= -5y
Ans.
- 2x+3y=9
2x+3y-9=0
Comparing the above equation with ax + by + c = 0
a = 2
b = 3
c = -9
- x- y/5-10=0
Comparing the above equation with ax + by + c = 0
a = 1
b = -1/5
c = - 10
- x=3y
x-3y=0
Comparing the above equation with ax + by + c = 0
a = 1
b = -3
c = 0
- 2x= -5y
2x+5y=0
Comparing the above equation with ax + by + c = 0
a = 2
b = 5
c = 0
Ques. Find out if the following equations belong to a consistent system or inconsistent system algebraically. (5 Marks)
2x + 5y = 0 and 4x + 10y = 0
3y + 4x – 2 = 0 and 6y + 3x + 7 = 0
Ans.
- 2x + 5y = 0 and 4x + 10y = 0
Comparing the first equation with ax + by + c = 0
a1 = 2
b1 = 5
c1 = 0
Comparing the second equation with ax + by + c = 0
a2 = 4
b2 = 10
c2 = 0
Comparing the values from both equations, we can conclude that they are algebraically dependent system
\(\frac{a1}{a2} = \frac{b1}{b2} = \frac{c1}{c2}\)
\(\frac{2}{4} = \frac{5}{10} = \frac{1}{2}\)
Note that here the c1 and c2 are zeros hence they are not considered. The given pair of equations belongs to the dependent system as it satisfies the dependent algebraic representation.
- 3y + 4x – 2 = 0 and 6y + 3x + 7 = 0
Comparing the first equation with ax + by + c = 0
a1 = 3
b1 = 4
c1 = - 2
Comparing the second equation with ax + by + c = 0
a2 = 6
b2 = 3
c2 = 7
Comparing the values from both equations, we can conclude that they are algebraically independent system
\(\frac{a1}{a2} ? \frac{b1}{b2}\)
\(\frac{3}{6} ? \frac{4}{3}\)
The given pair of equations belongs to the independent system as it satisfies the independent algebraic representation.
Ques. Draw the graph of each of the following linear equations in two variables: (5 Marks)
x + y = 4
x – y = 2
y = 3x
3 = 2x + y
Ans.
- x + y = 4
| x | y | (x, y) |
|---|---|---|
| 0 | 4 | (0, 4) |
| 4 | 0 | (4, 0) |

- x – y = 2
| x | y | (x, y) |
|---|---|---|
| 0 | -2 | (0, -2) |
| 2 | 0 | (2, 0) |

- y = 3x
| x | y | (x, y) |
|---|---|---|
| 2 | 6 | (2, 6) |
| 1 | 3 | (1, 3) |
| -1 | -3 | (-1, -3) |

- 3 = 2x + y
| x | y | (x, y) |
|---|---|---|
| -1 | 5 | (-1 5) |
| 0 | 3 | (0, 3) |
| 1 | 1 | (1, 1) |

Ques. In a Taxi, for the first kilometre, the fare is 8 and for the subsequent distance it is 5 per km. Taking the distance covered as x km and total fare as y, write a linear equation for this information, and draw its graph. (5 Marks)
Ans. As given in the question, the fare for the first km is Rs 8.
Let the total distance covered by the taxi be ‘x’ km
After the first km, the fare changes to Rs 5 per km for the rest of the distance.
Now, the taxi covers (x-1) distance at Rs 5 per km. while Rs 8 for the first km. Thus, the total fare will be ‘y’
y = 8 + (x - 1) 5
y = 8 + 5x – 5
y = 5x + 3
| x | y | (x, y) |
|---|---|---|
| 1 | 8 | (1, 8) |
| 0 | 3 | (0, 3) |

Ques. Derive the value of x and y from the following equations (5 Marks)
3x + 2y = 19
x + y = 8
Ans. Let’s consider,
3x + 2y = 19… (1)
x + y = 8 … (2)
Solving algebraically, we need to first eliminate any one term of the two equations
Thus for equating the equation (2) with eqn (1)
Multiplying eqn (2) with 2 we get the modified equation –
2x + 2y = 16 … (3)
Now subtract (3) from (1) we get,
x = 3 … (4)
substitute eqn (4) in eqn (2)
3 + y = 8
y = 5
Thus, the correct value of x and y is 3, 4.
Ques. Find the value of x, y, z from the following equations (5 Marks)
x + z = 6
z − 3y = 7
2x + y + 3z = 15
Ans. Let’s consider,
x + z = 6 … (1)
z − 3y = 7 … (2)
2x + y + 3z = 15 … (3)
Eqn (1) can also be written as x = 6 – z
We can replace x in eqn (3) by 6 – z
2 (6 - z) + y + 3z = 15
12 – 2z + y + 3z = 15
y + z = 3 … (4)
eqn (4) can also be written as z = 3 – y
we can substitute z = 3 – y in eqn (2)
(3 - y) – 3y = 7
3 – 4y = 7
-4y = 4
y = -1 … (5)
substitute eqn (5) in eqn (4)
-1 + z = 3
z = 4 … (6)
substitute eqn (6) in eqn (1)
x + 4 = 6
x = 2
Thus, the values of x, y, and z are 2, -1, and 4.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments