Area of a Trapezoid Formula with Example: Types, Derivation, Examples

Area of a Trapezoid can be calculated using the lengths of the two parallel sides and the height of the trapezoid. A trapezoid is a two-dimensional quadrilateral that has two sides parallel, known as bases and two non-parallel sides known as legs. Trapezoids can be of different types such as isosceles trapezoid, scalene trapezoid, acute trapezoid, obtuse trapezoid and right trapezoid. 

Key Terms: Area of Trapezoid, Isosceles Trapezoid, Acute Trapezoid, Obtuse Trapezoid, Right Trapezoid, Scalene Trapezoid

---

What is a Trapezoid?

[Click Here for Sample Questions]

Convex quadrilateral with at least one pair of parallel sides is known as Trapezoid or Trapezium. The other two sides are non-parallel. Parallel sides are called bases and non-parallel sides are called the legs or the lateral sides.

Line that connects the mid-points of two non-parallel sides is called the mid-segment. If a line segment is drawn between the two unequal lines the trapezium will be divided into two unequal segments.

Fig. Trapezoid 

---

Types of Trapezoids

[Click Here for Sample Questions]

There are different types of trapezoids. Examples of some of the important trapezoids are Isosceles trapezoids, scalene trapezoids and right-angled trapezoids

Based on Sides

Isosceles Trapezoids

When a trapezoid has two equal non-parallel sides, it is called an Isosceles trapezoid. In the above diagram, ABCD is an isosceles trapezoid where the non-parallel sides are equal i.e. AD=BC.

Fig: Isosceles Trapezoid

Scalene Trapezoid

A scalene trapezoid is a type of trapezoid whose sides and angles are unequal. In the above figure, ABCD is a scalene trapezoid where all the sides and all the angles are unequal.

Fig: Scalene Trapezoid 

Based on Angles

Acute Trapezoid

An acute trapezoid is a type of trapezoid that has two equal adjacent angles. Here, in case of trapezoid ABCD, ‹BAD= ‹CDA. Thus, it is an acute trapezoid.

Fig: Acute Trapezoid 

Obtuse Trapezoids

An obtuse trapezoid is a trapezoid in which two opposite angles are obtuse( >90°). In the above image ABCD is an obtuse trapezoid in which ‹ADC and ‹BCD both are obtuse.

Fig: Obtuse Trapezoid

Right Trapezoid

In the case of the Right trapezoid, the two adjacent angles are right angles. In the above given figure, ABCD is a Right trapezoid where ‹DAB and ‹CDA are both right angles.

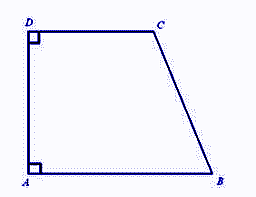
Fig. Right Trapezoid

---

Properties of Trapezoids

[Click Here for Sample Questions]

Here are some of the properties of a trapezoid:

• A trapezoid has two parallel and two non-parallel sides named as bases and legs respectively.
• Like other quadrilaterals the sum total of the interior angles of a trapezoid is always equal to 360°.
• In a trapezoid, the length of a midsegment is half of the total length of the parallel sides.
• In the case of an isosceles trapezoid the diagonals are equal in length.
• In a trapezium the adjacent angles formed in between the adjacent sides and one of the non-parallel sides are supplementary. 

---

Area of Trapezoids

[Click Here for Sample Questions]

The area of a trapezoid can be calculated using the lengths of the two parallel sides and the height of the trapezoid. The formula to compute the area(A) of a trapezoid using the base and the height is:

\(A = \frac{(a +b)}{2} .h\)

(Here, a and b are the lengths of the parallel sides and h is the height between them). 

---

Derivation of Trapezoids

[Click Here for Sample Questions]

Let us assume that ABCD is a trapezoid having two parallel sides AB and DC and two non-parallel sides namely DA and CB.

Fig. Derivation of Trapezoid Formula

Now, a perpendicular is drawn from the point D on the side AB, let DL= h.

AC divides the trapezoid ABCD into two equal triangles ADC and ABC.

So, the area of the trapezoid ABCD = Δ ADC + Δ ABC…………………………..(i)

Now, as DL=h is the altitude of the trapezoid ABCD, ‘h’ is the altitude of the ΔADC and ΔABC .

Therefore, the area of ΔADC = 1/2.DC.h

And, the area of Δ ABC = 1/2.AB.h

Substituting these values in (i) we get,

Area of Trapezoid ABCD = (1/2.DC.h) + (1/2.AB.h)

= 1/2( AB+DC).h

= 1/2( Sum of the parallel sides).(height between the parallel sides)

Thus, we get the formula of the trapezoid ABCD. 

---

Solved Examples

[Click Here for Sample Questions]

Find out the area of a trapezoid whose bases are 24cm and 32cm respectively and the perpendicular height is 7cm.

Solution: In this problem,

a= 24cm; b=32 cm; and h=7 cm

Applying the formula of the area of the trapezoid we get,

Area(A)=((a+b))/2.h = 1/2(24+32)7= 196cm²

There is a trapezoid-shaped garden nearby your house. Its two parallel bases are of 26 m and 40m each. If the area of the trapezoid is 3960 m2. Find out the distance between the parallel bases of the garden.

Solution: As given,

a= 26m: b=40m and area A= 3960m²

Let ‘h’ be the distance between the parallel bases.

As per the formula of trapezoid,

Area (A)=((a+b))/2.h 

Rearranging it we will get,

h= (2 A)/((a+b))

 = (2(3960))/((26+40) )

=7920/66

=120

Therefore, the distance between the parallel bases of the garden is 120m.

---

Things to Remember

[Click Here for Sample Questions]

• Trapezoids are the quadrilaterals where two of the sides are parallel to each other while the other two are not.
• If a line segment is drawn between the two unequal lines the trapezium will be divided into two unequal segments.
• Based on the side’s trapezoids can be of two types- Isosceles trapezoid (having equal non-parallels) and Scalene trapezoid (neither sides nor angles are equal).
• Based on the angle’s trapezoids are of three types- Acute trapezoid (having equal adjacent angles), Obtuse trapezoids (where two opposite angles are >90°) and Right Trapezoids (where adjacent angles are 90°).
• The area of a trapezoid can be calculated using the lengths of the parallel sides and the perpendicular distance between them.
• The formula to compute the area(A) of a trapezoid using the base and the height is
• (Where, a and b are the lengths of the parallel sides and h is the height between them) 
• In an isosceles trapezoid the diagonals are equal in length.
• The sum total of the interior angles of a trapezoid is always equal to 360°. 

---