
Collegedunia Team Content Curator
Content Curator
Codomain and Range are the terms that are related to functions. Functions are expressions, rules, or laws, that define a relation between two variables, where one variable is dependent on the other. Both of these terms are related to the output, so the term 'range' is sometimes used to refer to the term 'codomain'. But, there is a slight difference between the two.
| Table of Content |
Key Takeaways: Function, Codomain, Range, Domain, Variables, Sets, Subset
What is a function?
Functions are expressions, rules, or laws, that define a relation between two variables, where one variable is dependent on the other.
Function
Let us now take an example:
Let f be a function from a set A to a set B, to define a specific type of relationship for which every element x of set A has one and only one image y in set B.
We write f: A→B, where f(x) = y.
Here, A is the domain, and B is the codomain of the function f.
For example,
let A = {1, 2, 3, 4, 5, 8} and B = {1, 4, 8, 9, 25, 27, 64, 125}.
The function f: A → B is defined by f (x) = x².
So here,
Domain = Set A
Codomain = Set B, and
Range (R) = {1, 4, 9, 25, 64}
The range should be a square of set A, but the square of 4 (that is, 16) is not present in set B, so we have 8 in the domain, but we don’t have 16 either in the codomain or range. The range is the subset of the codomain.

Domain and Range
Also Read: Different kinds of relations
Domain, Codomain, and Range
A domain is a group of possible values that the independent variable of the function can take. This means that domain refers to the set of all the possible values that ‘x’ can take in the function f. A domain is a set of pre-images.

Domain and Codomain
A codomain is the group of possible values that the dependent variable of the function can take. This means that the codomain refers to the set of all the possible values that ‘y’ can take in the function f. A codomain is a set of images.

Range and Codomain
The range is a group of all the elements from set B that have the corresponding pre-image in set A. This means that a range refers to the set of all the possible values of the function that we receive upon taking the different values of x in the function f.
Read More: Types of functions
For the example given for the two sets, A = {1, 2, 3, 4, 5, 8} and B = {1, 4, 8, 9, 25, 27, 64, 125}, the function f: A → B is defined by f (x) = x².
According to the example taken above, set A is the domain of the function, B is the codomain of the function and the set {1, 4, 9, 25, 64} is the range of the function.
Also Read:
Difference between Codomain and Range
The key differences between Codomain and Range are tabulated below.
| Codomain | Range |
|---|---|
| Codomain is referred to as the range of function along with a few additional values. | The range is defined as the subset of the codomain |
| The codomain of a function restricts its output. | The range of a function does not restrict its output and can be used exactly as the codomain. |
| Codomain is the set of all the possible values that might come out of it. | The range is the actual, definitive set of values that might come out of it. |
| The codomain of a function refers to its definition or its meaning. | The range refers to the image of a function. |
Things to Remember
- Codomain is simply the possible value of the output of the function.
- The range is a set of the exact values of the output of the function.
- The range is a subset of the codomain of a function.
- The number of elements of the range can never be more than the number of elements of the codomain.
- The denominator of a function can never be zero.
- A real function has the set of real numbers or one of its subsets both as to its domain and range.
Also Read:
Sample Questions
Ques. When are the codomain and the range of a function equal? (2 marks)
Ans: The domain and codomain of a function are equal when the number of the elements in its range is equal to the number of elements in its codomain. This means that for any function every element of set A has its image in set B.
So, if every element of the codomain is also present in the range of the function, both of them will become equal.
Ques. In what conditions will the range of the function be greater than its codomain? (2 marks)
Ans: The range is a subset of the codomain for any function. We already know that a subset can never be greater than the universal set. This means that the number of elements in the range of a function can never be greater than its codomain. The range can either be smaller than or equal to the codomain, but it can never be greater than the codomain.
Ques. Is it possible for the domain, range, and codomain of a function to be equal to one another? (2 marks)
Ans: Yes, it is possible for the domain, range, and codomain of a function to be equal to one another.
The domain will be equal to the codomain if its elements have their image present in the codomain.
The codomain and range will be equal if every element of the codomain is also present in the range of the function.
Also Read:
| Area of a Triangle | Minors and Cofactors of determinants | Continuity and Differentiability of a function |
Ques. What are the differences between codomain and range? (3 marks)
Ans: The following are a few differences between codomain and range:
- Codomain is referred to as the range of function along with a few additional values. On the other hand, the range is defined as the subset of the codomain.
- The codomain of a function restricts its output. Whereas, the range of a function does not restrict its output and can be used exactly as the codomain.
- Codomain is the set of all the possible values that might come out of it. Whereas, the range is the actual, definitive set of values that might come out of it.
- The codomain of a function refers to its definition or its meaning. On the other hand, the range refers to the image of a function.
Ques. Determine the domain and range of the relation R defined by R = {x – 2, 2x + 3} : x ∈ {0, 1, 2, 3, 4, 5} (3 marks)
Ans. Given x = {0, 1, 2, 3, 4, 5}
x = 0 ⇒ x – 2 = 0 – 2 = -2 and 2x + 3 = 2*0 + 3 = 3
x = 1 ⇒ x-2 = 1-2 = -1 and 2x+3 = 2*1+3 = 5
x = 2 ⇒ x-2 = 2-2 = 0 and 2x+3 = 2*2+3 = 7
x = 3 ⇒ x-2 = 3-2 = 1 ad 2x+3 = 2*3+3 = 9
x = 4 ⇒ x-2 = 4-2 = 2 and 2x+3 = 2*4+3 = 11
x = 5 ⇒ x-2 = 5-2 =3 and 2x+3 = 2*5+3 = 13
Hence R = {-2, 3), (-1, 5), (0, 7), (1, 9), (2, 11), (3, 13)
Domain of R = {-2, -1, 0, 1, 2, 3}
Range of R = {3, 5, 7, 9, 11, 13}
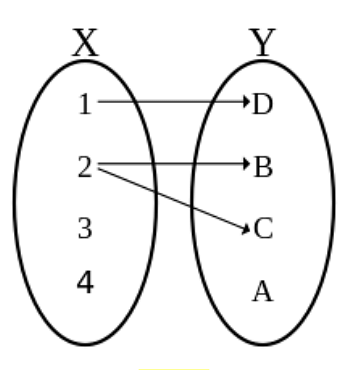
Ques. The below figure shows a relation between Set x and Set y. Write the same in Roster Form, Set Builder Form, and find the domain and Range? (2 marks)
Ans.

In the Set Builder Form R = {(x, y): x is the square of y, x ∈ X, y ∈ Y}
In Roster Form R = {(2, 1)(4, 2)}
Domain = {2, 4}
Range = {1, 2}
Also Read:
Ques. State the domain and range of the following relation: (eye color, student’s name). A = {(blue, John), (green, William), (brown,Wilson), (blue, Moy), (brown, Abraham), (green, Dutt)}. State whether the relation is a function? (2 marks)
Ans. Domain: {blue, green, brown} Range: {John, William, Wilson, Moy, Abraham, Dutt}
No, the relation is not a function since the eye colors are repeated.
Ques. The Arrow Diagram Shows the Relation R from Set C to Set D. Write the relation R in Roster Form? (2 marks)

Ans. We observe the relation R using the Arrow Diagram Above
From that Relation R in Roster Form = {(2,20) ; (2, 40) ; (4, 40) ; (3, 30)}
Ques. State the domain and range of the following relation: {(4,3), (-1,7), (2,-3), (7,5), (6,-2)}? (2 marks)
Ans. The domain is the first component of the ordered pairs. Whereas, Range is the Second Component of the ordered pairs. Remove the duplicates if any are present.
Domain = {4, -1, 2, 7, 6} Range = {3, 7, -3, 5, -2}
Ques. From the following Arrow Diagram find the Domain and Range and depict the relation between them? (2 marks)
Ans. 
Domain = {3, 4, 5}
Range = {3, 4, 5, 6}
R = {(3, 4), (4, 6), (5, 3), (5, 5)}
- Determine the domain and range of the relation R defined by
R = {x – 2, 2x + 3} : x ∈ {0, 1, 2, 3, 4, 5}
Also Read:







Comments