
Collegedunia Team Content Curator
Content Curator
Bijective function is a function f: A→B if it is both injective and surjective. A function is surjective or onto if for every member b of the codomain B, there exists at least one member of domain A such that f(a) = b. A function is injective or one-to-one if for every member b of the codomain B, there is at most one a that is a member of domain A such that f(a) = b.
| Table of Content |
Key Takeaways: Bijective function, injective function, surjective function
What is a Bijective Function?
[Click Here for Sample Questions]
Bijective function is both a one-to-one or injective function, and an onto or surjective function. This means that for every function f: A → B, each member a of domain A maps to precisely one unique member b of codomain B.
Bijective Function
Also Read:
Properties of Bijective Function
[Click Here for Sample Questions]
There are certain features that make a bijective function:
- There is an equal number of members in the domain and codomain sets of a bijective function.
- A bijective graph meets any horizontal or vertical line drawn across it only once - no more, no less.
- In a bijective function, the cardinality of the sets are maintained.
- The range of a bijective function f: A→B is the same as its codomain, because the function gives the same results as the image of the codomain.
- In a bijective function f: A → B, each element of set A should be paired with just one element of set B and no more than that, and vice versa.
Differences Between Injective, Surjective and Bijective Functions
[Click Here for Sample Questions]
The key differences between injective, surjective and bijective functions are tabulated below.
| Injective (one to one) function | Surjective (onto) function | Bijective function |
|---|---|---|
 |  |  |
| Each element in codomain Y is mapped to by at most one element in domain X, it could be none. | Each element in domain X maps onto at least one element in domain Y, it could be more than one element mapping onto the same element. | Each element in domain X maps to exactly one unique element of codomain Y. |
| Range is not equal to codomain. | Range is equal to the codomain. | Bijective functions have an inverse. |
Here’s a summary:
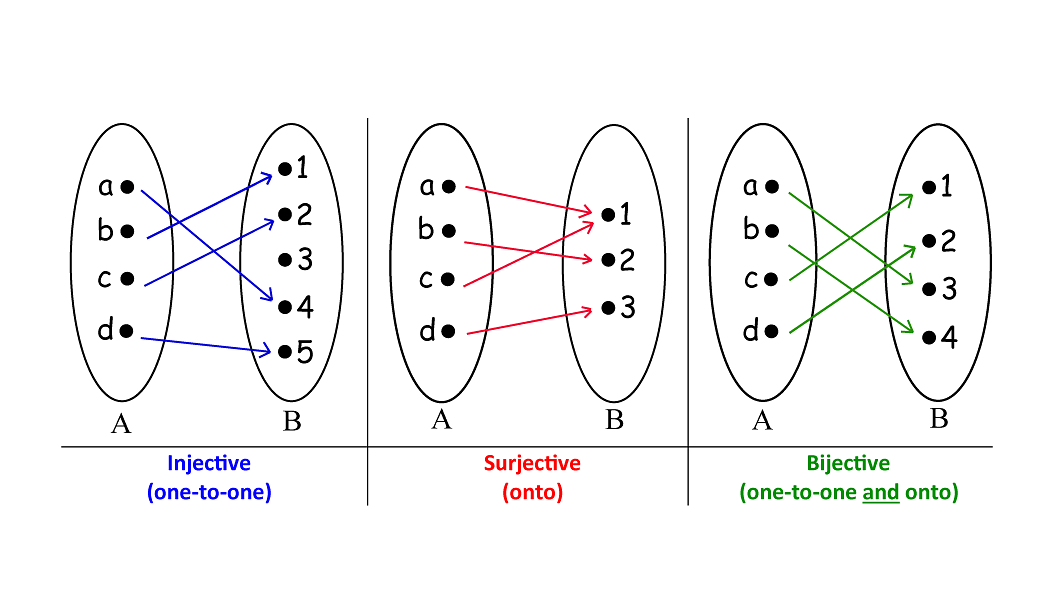
Differences Between Injective, Surjective and Bijective Functions
Proving that a Function is Bijective
[Click Here for Sample Questions]
To prove that a function is bijective, we’ll be looking at an example:
Given f: R → R, f(x) = x3. Prove that f(x) is a bijection.
To prove that a function is a bijection, we have to prove that it’s an injection and a surjection.
To prove that it’s an injection, we use this test:
f(a) = f(b) = a = b (if this is true for the function then it’s an injection)
In this case, we have
a3 = b3
So, since they’re both cubed, we have
a = b
Therefore, this is an injection.
For surjection, we have to check whether the range equals the codomain.
range of x3 = codomain R
In other terms, all the elements n in the codomain have a corresponding element \(\sqrt n\) in the domain. And this is true in this case.
Since this function is both injective and surjective, we have proven that it’s bijective.
Things to Remember
[Click Here for Sample Questions]
- A bijective function is one that’s both injective and surjective.
- The differences between injective, surjective, and bijective functions lie in how their codomains are mapped from their domains.
- There are rules to prove that a function is bijective.
- The range is the elements in the codomain.
- In a bijective function range = codomain.
Also Read:
Sample Questions
Ques 1: Is f: R → R defined as f(x) = 3x3 + 5 bijective? (2 marks)
Ans: Check for injection and surjection.
For injection
f(x) = f(y), so in this case, we consider:
3x3 + 5 = 3y3 + 5
Simplify this equation and we’ll get:
3x3= 3y3
x = y
So this is an injection.
For surjection,
let y be an element of R
Then f(x) = y, so 3x3 + 5 = y
x = 3y-53
f(x) = f(3y-53)
Simplify this and we get,
f(x) = y
So this is a surjection.
Now that we have proven that it’s both an injection and a surjection, we can conclude that it’s a bijection.
Ques 2: Let A = {x\(\in\)R:-1<x<1} = B. Show that f: A → B given by f(x) = x|x| is a bijection. (2 marks)
Ans: Let x, y A. Then,
x\(\neq\) y , x|x|\(\neq\) y|y|, f(x) f(y)
This shows that f: A → B is an injection
To prove surjection, we need to show that every element in the codomain has a preimage. So,
For f(x) = x|x|, if 0x1 , its value will be x2. And if -1x < 0, its value will be -x2.
Every value on the x-axis has the same value on the y-axis, so this is a surjection.
Since this function is both a surjection and injection, we have proven that it’s a bijection.
Ques 3: Let U be any set with elements in it. Prove that the identity function on set U is an injection. (2 marks)
Ans: I: U → U. The function : I(x) = x. To be an injection,
I(x) = I(y); x,y\(\in\) U
x = y so the set is a one- to - one or injective function.
Ques 4: Let K be any set with elements in it. Prove that the identity function on set K is a surjection. (2 marks)
Ans: I: K → K. The function: I(x) = (x). Checking if it’s a surjection,
Let y\(\in\) K
I(x) = y
The function is a surjection.
Ques 5: For f: N -{1} → N is defined by f(n) being the highest prime factor of n, show that f is neither surjective nor injective. (2 marks)
Ans: It’s not surjective because the range is just prime numbers, while the codomain is N which could include numbers other than prime numbers. Since codomain is not equal to range, we can conclude that it’s not surjective.
To prove it’s not injective, we can try inputting random numbers into the function.
f(6) = 3
f(9) = 3
f(12) = 3
The largest prime factor of all these numbers is 3. The number is repeated so it’s not injective.
Ques 6: What’s the difference between range and codomain? (2 marks)
Ans: The codomain is the set of all the values that could possibly come out after the mapping of a function while the range is the set of values that do come out.
Ques 7: How to differentiate between injective, surjective, and bijective functions? (2 marks)
Ans:
- In injective functions, one element from the domain will point to exactly one unique element from the codomain. There can be elements in the codomain that are left out.
- In surjective functions, there won’t be any elements in the codomain that are unpaired and that there will be at least one element from the domain pointing to one element in the codomain. There could be more than one too, unlike in injective functions.
- In bijective functions, every element has one pairing and none of the elements on both sets are left out. Bijective functions can be inverted: every element in the domain maps into a unique element in the codomain and back.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:







Comments