
Content Strategy Manager
Difference between relation and function is that a relation consists of many outputs for a single input, while a function can only have one single input for a single output. Relation and functions are integral mathematical tools.
- Relation and functions are useful to solve equations with elements having a 'cause and effect' dependent relation.
- In algebra, relation and function are connected to the set of any ordered pairs. By assigning one input in relation and function, it is possible to find out many or one outputs that satisfy the conditions.
- There are different ways to represent them such as, sets, two-variable equations, dimensional graphs etc.
- A relation is simply a connection of two sets by any means. It is a collection of ordered pairs which have elements from one set to another.
- A function is a relation which defines the set of inputs to the set of outputs.
Read Also: Remainder Theorem
| Table of Content |
Key Terms: Relation, Functions, Graph, Equations, Cartesian Product, Sets, Range, Domain, Ordered Pairs, Onto Functions, Binary Division
What is a Relation?
[Click Here for Sample Questions]
The term relation defines the dependency between sets of any ordered pairs. A relation from set A to set B can be expressed as a subset of the cartesian product set A x B. The subset is composed of a relationship between the first and the second element of elements in A x B.
- An example of Relation is: R = {(1,2), (2, -3), (3,5)}
- The first element of the ordered pairs is in the first set. The first set is called Domain.
- The second element of the ordered pairs is in the second set. The second set is called Range.
Ordered Pairs
The term ordered pairs refers to a pair of two objects that come in a certain order after one another. It is different when the objects change their respective places.
Example: (a,b) is an ordered pair where a and b both are specified.
Similarly, (b, a) is an ordered pair where b and a both are specified to their place.
Unless a = b, (a,b) is not equal to (b,a)
Cartesian Products
The cartesian product makes up a set that contains objects from 2 sets in relation.
The first object of ordered pairs, in this case, comes from the domain (Let’s say A) and the second one comes from range (Let’s say B). This is called the cartesian product of (A X B).
Hence, H(A x B) = {(a,b):a ∈ A ^ b ∈ B}
Example: A = {1,2,3}, B = {4,5}
Then, the cartesian product is,
(A X B) = R = {(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)} is of A to B i.e ARB.
Also Read:
Types of Relation
[Click Here for Previous Year Questions]
There are five different kinds of relations. They are:
Empty relation
Empty relation is when there is no related element of domain to range. ARB=(null)
Universal relation
When there is a related element to range for every element in the domain, it is then known as Universal Relation.
Reflexive relation
For Reflexive Relation, if (a, a) ∈ R, for every a ∈ A.
Symmetric relation
In case of Symmetric Relation, if (a1 , a2 ) ∈ R implies that (a2 , a1 ) ∈ R, for all a1 , a2 ∈ A.
Transitive relation
For a Transitive Relation, if (a1 , a2 ) ∈ R and (a2 , a3 ) ∈ R implies that (a1 , a3 ) ∈ R, for all a1 , a2 , a3 ∈ A.
Equivalence Relation
Equivalence relation is when the relation is symmetric, transitive and reflexive at the same.
Identity Relation
An identity relation is when every element of a set returns the same value of itself.
Identity relation is denoted by ‘I’.
R = {(a,a):aA} [A is a set]
Example: If a set A = {a,b,c}, the identity relation of A is I = {(a,a),(b,b),(c,c)}
It concludes that Identity relation is from A to A.
Inverse Relation
An inverse relation is a relation that is obtained by interchanging the ordered pair.
R = {(a,b):aA,bB}
Then,
R-¹ = {(b,a):aA,bB}
Example: If R is the relation of set A = {a,b,c} & B = {2,3,4},
The inverse relation or R-1is {(2,a),(3,a),(4,a),(2,b),(3,b),(4,b),(2,c),(3,c),(4,c)}
Relation and Functions Detailed Video Explanation
Also read:
What is a Function?
[Click Here for Sample Questions]
A function is simply a kind of relation. It is a relation wherein every domain value maps one range value. Function establishes a relation between two sets i.e. domain and range with only one object in the range for a specific object in the domain. It is represented by ƒ: X ⇒ Y. In function, for one input, we can get only one output.
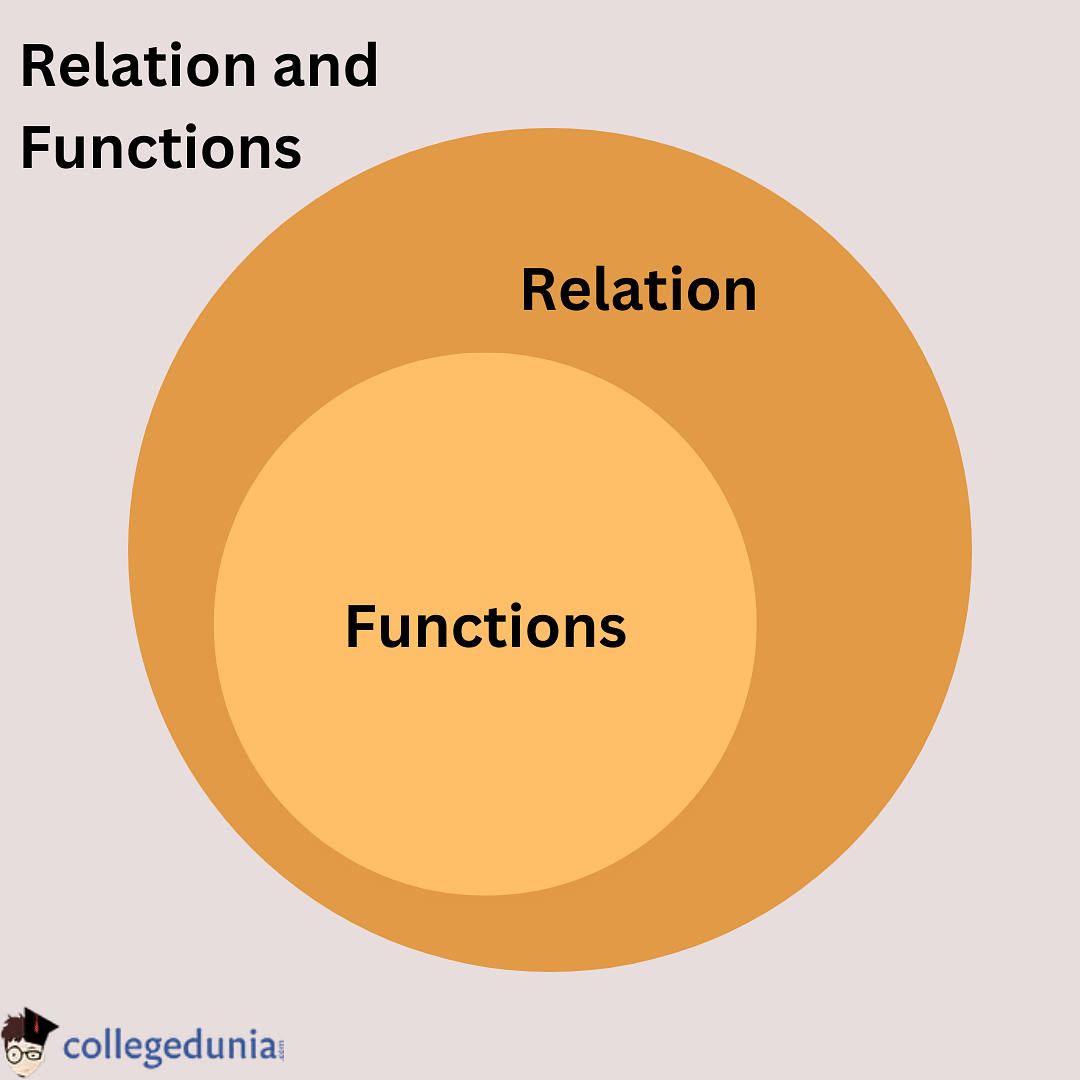
Relations and Functions
Example of Functions
In your class, there is a relation between you and your math marks. You can have different marks in different exams. Suppose you get 50 in the first exam, 30 in the second exam, both the marks establish a relation between you and maths marks.
Consider only the first exam, where you got 50 marks. Now, you can say, there is a function between you and your grades. As for one input (first exam), you have only one output (50 marks).
Also Check: Correlation Coefficient Formula
Types of Function
[Click Here for Previous Year Questions]
The different types of functions are as follows.
- Injective or one-one function: A function is said to be injective when that function maps out unique elements of the domain to unique elements of the range.
- Surjective or onto function: A function is said to be surjective when every element of range maps out an element in the domain.
- Bijective or one-one & onto: A function is said to be bijective when it is both injective and surjective.
- Many-to-one function: A function is said to be many-to-one when 2 or more elements (input) of a domain have the same image (output) in range.
Read More: Ceiling Function
Difference between Relation and Function
[Click Here for Sample Questions]
The key differences between Relations and functions are tabulated below.
| Parameters | Relation | Function |
|---|---|---|
| Definition | In relation, the connection between ordered pairs doesn’t have to be distinct. | For functions, the connection between ordered pairs is specific. |
| Number of relation | For one object/element in a domain, there are many objects/elements in the range. | For one object in the domain, there is only one object in the range. |
| Methods | Mathematically, the Relation between two sets can be found through cartesian products. | The function between two sets can be found through equations, graphs etc. |
| Dependability | All Relations are not a function. | All functions are a relation. |
Things to Remember
- Relation describes the connection between collections of sets of ordered pairs that are in domain & range respectively.
- In a relation, for one object/element in a domain, there are many objects/elements in the range.
- The function is a relation with a specific rule of only one element to range for one element in the domain.
- All functions are a relation but all relations are not functions.
- A relation is generally denoted by ‘R’ & Function by ‘F’ or ‘f’.
Read More: NCERT Solutions Class 12 Mathematics Relations and Functions
Previous Year Questions
- (x−1)(x2−5x+7)<(x−,1) then x belongs to… [BITSAT 2007]
- Consider the following lists… [AP EAPCET]
- If a+π/2<2tan−1… [KCET 2019]
- If FF is function such that F(0)=2,F(1)=3...
- Satisfies the functional equation f(x−y)=f(x)f(y)...
- The set {x:f(x)=f−1(x)}={1,2}{x:f(x)=f−1(x)}={1,2} f is a bijection and f−1(x)=1+√x−1,x≥1...
- If A={x|x∈N,x≤5},B={x|x∈Z,x2−5x+6=0}… [KCET 2019]
- f : R → R and g : [0, ∞) → R is defined by… [KCET 2019]
- cos[2sin−13/4 + cos−13/4] =… [KCET 2019]
- On the set of positive rationals, a binary operation… [KCET 2019]
Also Check Out:
Sample Questions
Ques: Let N be the set of natural numbers and R be the relation in N defined as R = {(a, b) : a = b – 2, b > 6}. (2 marks)
Ans: As the relation given in the question, b>6.
So, we can confirm that option A) isn’t the solution.
Now, when b>6, a=(b-2).
Therefore, b=8, a=(8-2)=6.
Ques: If f:R → R is defined by f(x)=3x+2, then define f[f(x)] (CBSE 2010) (2 marks)
Ans: f(x)=3x+2
f[f(x)]=f(3x+2)=3(3x+2)+2=(9x+8)
Ques: If R={(x,y):x+2y=8} is a relation on N, then write the range of R. (2 marks)
Ans: Given, X + 2Y = 8
Or, X = 8 - 2Y
Since, X, Y∈ N ; Y=1, X=6; Y=2, X=4; Y=3, X=2
R={(6,1),(4,2),(2,3)}
Therefore, the range of R is {1,2,3}.
Ques: If the function f:RR defined by f(x)=(3x-4) is invertible, find f-1. (CBSE 2010) (2 marks)
Ans: Given, f(x)=(3x-4) & is invertible.
Let, y=(3x-4)
x=\(\frac{(y+4)}{3}\)
f-1(y)=\(\frac{(y+4)}{3}\)
f-1(x)=\(\frac{(x+4)}{3}\)
Ques: State whether the function f: NN is given by f(x) = 5x is injective, surjective or both. (CBSE 2008) (2 marks)
Ans: Given, f(x)=5x
Let, f(x1)=f(x2)
5x1=5x2
x1=x2x1,x2N
So, f(x) is an injective function.
Range of f(n)=5n, nN
But codomain=N
∴Range≠ codomain
∴f(x) is not surjective.
Hence, the given function is injective.
Ques: f f,g :RR are two functions defined as f(x) = |x| + x & g(x) = |x|-x, xR. Find fg & gf. (CBSE 2014) (2 marks)
Ans: Given, f(x)=|x|+x & g(x)=|x|-x for all xR
f(x)={2x,x>0} & g(x)={0, x>0}
{0, x<0} {-2x,x<0}
Thus for, x>0, gf=g(2x)=0
f og=f(0)=0
For x<0, gof=g(0)=0
fog=f(-2x)=-4x
∴ gof(x)=0, xR
fog={-4x, x<0}
{0, x>0}
Ques: If A = R-{2} & B=R-{1}. If f:AB is a function defined by f(x)=\(\frac{x-1}{x-2}\), then show f is one-to-one & onto. Find f-1. (CBSE 2013) (5 marks)
Ans: Given,f(x)=\(\frac{x-1}{x-2}\)& f:AB ,where A=R-{2} & B=R-{1}
One-one, Let, f(x1)=f(x2) x1x2∈A
\(\frac{x_1-1}{x_1-2}=\frac{x_2-1}{x_2-2}\)
(x1-1)(x2-2)=(x2-1)(x1-2)
(-x1)=(-x2)x1=x2
∴ f(x1)=f(x2) f(x1)=f(x2) x1x2∈A
Therefore,f(x) is one-one.
Onto, Let,y=\(\frac{x-1}{x-2}\)⇒(xy-2y) = (x-1)
x(y-1)=(2y-1)
x=\(\frac{(2y-1)}{(y-1)}\) ………..(i)
Since, xR-{2}, y∈R-{1}
So, range of f(x)=R-{1}
∴Range=codomain
Therefore,f(x) is onto.
From eq. (i), f-1(y)=\(\frac{(2y-1)}{(y-1)}\)
f-1(x)=\(\frac{(2x-1)}{(x-1)}\)
Ques: Show that f:N→N given by f(x)={x+1, if x is odd {x-1, if x is even, is bijective. (CBSE 2012) (5 marks)
Ans: Given f: NN such that
f(x)={x+1, if x is odd
{x-1, if x is even
One-one from the function,
1) When x is odd,
Let, f(x1)=f(x2)
(x1+1)=(x2+1)
(x1)=(x2)
So, f(x1)=f(x2)
(x1)=(x2),x1,x2∈N
2) When x is even,
Let, f(x1)=f(x2)
(x1-1)=(x2-1)
(x1)=(x2)
So, f(x1)=f(x2)
(x1)=(x2),x1,x2∈N
∴Both f(x) of 1) & 2) are one-one.
So, f(x1)=f(x2)
(x1)=(x2),x1,x2N
Therefore, f(x) is one-one.
Onto, for f(x) to be onto we have to show range & codomain are same.
f(1)=1+1=2
f(2)=2-1=1; (f(x)=(x-1),even)
f(3)=3+1=4
f(4)=4-1=3, etc.
∴Range of f(x)=N(natural numbers)
And given, that codomain=N
Thus, Range=Codomain
Therefore, f(x) is an onto function.
Hence,f(x) is bijective.
Ques: If the function f: R→R given by f(x)=x2+3x+1 & g: R→R is given by g(x)=2x-3 then find i)fog ii)gof (CBSE 2009, 2008) (2 marks)
Ans: 2 given equations are f(x)=x2+3x+1,when f:R→R & g(x)=2x-3 when g:RR.
i)fog (x)=f[g(x)]=f(2x-3)=(2x-3)2+3(2x-3)+1
=(4x2 - 6x + 1)
ii)gof (x)=g[f(x)]=g(x2+3x+1)=[2(x2+3x+1)-3]
=(2x2+6x-1)
Ques: If f:R→R is defined by f(x)=(4x3+7), show that f is a bijection. (CBSE 2011C) (5 marks)
Ans: The function f(x)=(4x3 + 7) when f:RR,
One-one- f(x1) = f(x2)
⇒(4 x13 + 7)=(4x23 + 7)
⇒x13 – x23 = 0
⇒(x1-x2)(x12 + x1x2 + x22) = 0
Either (x1 – x2) = 0….(i)
or,(x12 + x1x2 + x22) = 0….(ii)
Eq. (ii) isn’t possible.
So, (x1 – x2) = 0 ⇒x1 = x2
Thus, f(x1) = f(x2)
⇒x1 = x2x1, x2 ∈R
Therefore, f(x) is a one-one function.
Onto, to show f(x) is a onto function,
Range of f(x) = codomain of f(x)
Let, y=(4x3 + 7)
Or, x = \((\frac{y-7}{4}) ^{\frac{1}{3}}\)…..(iii)
Eq. (iii) shows that the range of f(x)=R, yR
Range of f(x)=codomain of f(x)
∴f(x) is an onto function.
Thus, f(x) is a bijective function.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments