
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Cosecant Function in Trigonometry is one of the oldest mathematical functions. The fundamental illustration of this function for real arguments is that "the cosecant of an angle α in a right?angled triangle is equivalent to the ratio of the length of the hypotenuse to the length of the opposite leg or opposite side." Also, the cosecant function is the reciprocal of the sine function. The branch of mathematics concerned with distinct functions of angles and their application to calculations is termed Trigonometry. There are typically 6 functions of an angle used in trigonometry names and abbreviations of which are as follows: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), cosecant (csc).
| Table of Contents |
Key Terms: Trigonometry, Trigonometric Functions, Angles, sine, cosine, tangent, cotangent, secant, cosecant, Geometry, Distance, Equilateral Triangle, Right-angled Triangle
What is Cosecant Function?
[Click Here for Sample Questions]
Just like all trigonometric functions, cosecant is based on a right triangle and is abbreviated as 'csc'. It is typically the reciprocal of the sine function. For instance, in a given right-angled triangle, the sine function is the ratio of the opposite side and hypotenuse and the cosecant function is the ratio of the hypotenuse and opposite side.
Where side opposite to the right angle is termed the hypotenuse and the other two sides are termed legs. The angle used determines whether the sides of the triangle are opposite or adjacent.
The image below shows the graph of the cosecant function and how it is formulated:-

Cosecant function
There are numerous angle functions. They provide a relationship among the sides of the triangle based on the angles given.
The cosecant function is the ratio of the hypotenuse and the opposite side of a right-angled triangle. In simpler terms, it is the reciprocal of sine i.e.
csc θ = 1/sinθ
Read More: Domain and Range of Trigonometric Functions
Cosecant Equation
[Click Here for Sample Questions]
Since the equation of sine function is known to us i.e. sin θ = opposite side/hypotenuse, we can easily evaluate the equation for cosecant function as follows:
csc θ = hypotenuse / opposite side
Considering the 45-45-90 triangle and 30-60-90 triangle as shown in the picture below, let's determine the cosecant function of the angles.

Cosecant Equation
In the first right triangle, the hypotenuse is given as √2
We know,
csc θ = hypotenuse / opposite side
On equating the values of the hypotenuse and θ in the above equation we get,
csc 45= √2 / 1
=>√2
In the second equilateral triangle, the given value of hypotenuse is 2
Using the formula of cosecant,
csc 60 = hypotenuse / opposite side
= 2/√3
csc 60 = 2 / 1
=> 2
Read More: Pythagoras Theorem
How to Graph a Cosecant Function?
[Click Here for Sample Questions]
We can easily determine the graph for cosecant function by the reasoning of the sine graph. The graph for the sine function is shown in the image below.

Sine Function Graph
By using the sine graph above we can use the values of the sine function at different intervals for determining the graph of cosecant function.
This means
- When the value of θ = 0, sin θ = 0. Since the value of csc 0 = not defined, we cannot evaluate csc θ.
- When the value of θ = 90, sin θ = 1, csc θ = 1
- When the value of θ = −90, sin θ = −1, csc θ = −1
- When the value of θ = ±180, sin θ = 0. Because the value of csc 0 = not defined
- When θ = ±270, sin θ = −1, csc θ = ±1
- If the value of θ is very small and positive then sin θ is positive and therefore, csc θ is large and positive.
- When the value of csc θ cannot be evaluated then we will get vertical asymptotes, i.e. at sin 0 and sin = nπ.
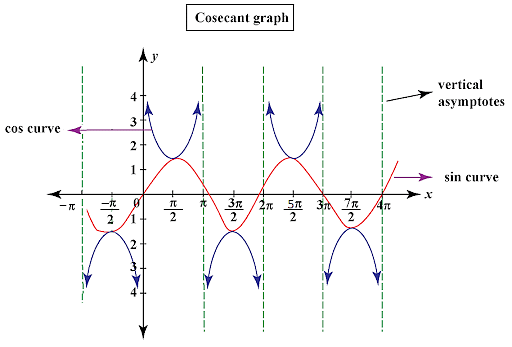
Cosecant Function Graph
Thus, we acquire the cosecant graph using a sine graph as demonstrated in the picture above. The graph has been plotted between the intervals of −π and 4π.
One of the important things to be noted is that the vertical asymptotes or the dotted lines in the graph for the csc function will appear at every multiple of π, i.e. at nπ, wherever the value of sin θ = 0.
Read More: Triangle Theorems
Things to Remember
- The cosecant function is the ratio of the hypotenuse and the opposite side of a right-angled triangle.
- The cosecant function is the reciprocal of the sine function. This implies when the sine approaches 0, then csc approaches infinity.
- The cosecant function is symmetrical around the x-axis is an odd function, i.e. csc(−θ) = - csc θ .
- Its graph includes duration of the length of 2π and has vertical asymptotes.
- The value of sine or cosecant relies on the value of sine in a way that when sine achieves its maximum value of 1 then cosecant arrives at its minimum value of 1 and vice-versa, likewise when sine is positive<1 then cosecant will be positive>1 and vice-versa.
Also Read:
Sample Questions
Ques. Prove that in the following equation, L.H.S = R.H.S (5 Marks)
Tan2θ + cot2θ + 2 = sec2θ.cosec2θ
Ans. From the above question,
L.H.S = Tan2θ + cot2θ + 2
= sec2θ - 1 + cosec2θ - 1 + 2
Using the identity, 1+ cot2θ = cosec2θ and 1+ tan2θ = sec2θ
We will get,
sec2θ + cosec2θ = (1/ cos2θ) + (1/ sin2θ)
=> (sin2θ + cos2θ) / (cos2θ. sin2θ)
=> 1 / (cos2θ. sin2θ) …(using identity sin2θ + cos2θ = 1)
=> sec2θ.cosec2θ = R.H.S
Hence, L.H.S = R.H.S
Ques. Solve the following equation for 0° < =90°: (5 Marks)
3 tan θ + cot θ = 5 cosec θ
Ans. According to the question, 3 tan θ + cot θ = 5 cosec θ
=> 3 tan θ + 1/tan θ = 5 cosec θ
=> 3 tan2θ + 1 = 5 cosec θ.tan θ
=> 3 tan2 θ + 1 = 5 sec θ
=> 3(sec2 θ – 1) = 5 sec θ
=> 3 sec2 θ – 5 sec2 θ – 2 = 0
=> sec θ = [5 +- √(25+24) ] / 6 = (5 +- 7) / 6
=> sec θ = 2 or -1/3
As -1< cos θ < 1 so, sec θ =! -1/3
Therefore, θ = 60° for 0°< θ <= 90°
Ques. Prove the following equation: (5 Marks)
(1+ cot θ – cosec θ) (1+ tan θ+ sec θ) = 2
Ans. As per the given question,
L.H.S = (1+ cot θ – cosec θ) (1+ tan θ+ sec θ)
=> (1 + (cos θ/ sin θ) – 1/ sin θ) (1 + (sin θ/cos θ) + 1/cos θ)
=> (sin θ + cos θ – 1) / sin θ) ((sin θ + cos θ + 1) / cos θ)
=> ((sin θ + cos θ)2 – 1 ) / sin θ. cos θ
=> (2 sin θ. cos θ + sin2 θ + cos2 θ - 1) / sin θ. cos θ
=> (1 + 2 sin θ. cos θ - 1) / (sin θ. cos θ)
=> (2 sin θ. cos θ) / sin θ. cos θ
=> 2 = R.H.S
Hence, L.H.S = R.H.S
Ques. If cosec θ - sin θ = a, and sec θ - cos θ = b. Prove the following equation: (5 Marks)
a2 b2 (a2 + b2 + 3) = 1
Ans. From the given question,
L.H.S = a2 b2 (a2 + b2 + 3)
=> (cosec θ - sin θ)2 (sec θ – cos θ)2 [(cosec θ - sin θ)2 + (sec θ – cos θ)2 + 3]
=> (cosec θ - sin θ)2 (sec θ – cos θ)2 [cosec2 θ + sin2 θ – 2 cosec θ.sin θ + sec2 θ + cos2 θ – 2 sec θ.cos θ + 3]
=> (cosec θ - sin θ)2 (sec θ – cos θ)2 [cosec2 θ + 1 – 2 + sec2 θ – 2 + 3]
=> (cosec θ - sin θ)2 (sec θ – cos θ)2 (cosec2 θ + sec2 θ)
=> [(1/ sin θ) - sin θ]2 [(1/cos θ)- cos θ]2 [(1/ sin2 θ) + (1/cos2 θ)]
=> [(1- sin2 θ)/ sin θ] [(1- cos2 θ)/ cos θ] [(sin2 θ + cos2 θ)/ sin2 θ. cos2 θ]
=> (cos2 θ / sin θ) (sin2 θ / cos θ) (1/ sin2 θ cos2 θ)
=> (cos4 θ / sin2 θ) * (sin4 θ /cos2 θ) * (1/ sin2 θ cos2 θ)
=> 1 = R.H.S
Hence proved L.H.S = R.H.S
Ques. What is the Pythagoras theorem? What are Pythagorean identities? (5 Marks)
Ans. In mathematics, the Pythagorean theorem typically known as Pythagoras theorem, is a basic relation in Euclidean geometry among the 3 sides of a right-angled triangle. As per this theorem, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides of the triangle. In a right-angled triangle, a hypotenuse is the longest side of the triangle, the side opposite to the right angle.
The Pythagoras theorem expressed in the form of trigonometry functions is said to be Pythagorean identity. There are mainly three pythagorean identities:
- Sin2θ+Cos2θ= 1
- 1+tan2θ = sec2θ
- cosec2θ = 1 + cot2θ
These three identities are of huge significance in Mathematics, as most of the trigonometry problems in exams are based on them.
Ques. What are some properties of cosecant function? (5 Marks)
Ans. A few of the important properties of cosecant function have been mentioned in the list below:
- It is an odd function as they have origin symmetry.
- The range of cosecant function given as y <= -1 or y >= 1
- csc x possesses a period equal to 2π.
- csc(x) has vertical asymptotes at all values of x = nπ, n being an integer.
- The domain of csc(x) is the set of all real numbers except x = nπ, n being an integer.
- csc(x) is an odd function and its graph is symmetric to the origin of the system of axes.
Ques. Given angles x and y in quadrant 1, and given, (3 Marks)
Sin x=3/5 and cos y=5/13.
Find the value of csc(x+y).
Ans. Use the following trigonometric identity to solve this problem.
csc(x+y) = 1/sin(x+y)
=> 1/ (sin x cos y + cos x sin y)
Using the Pythagorean triple 3, 4, 5, it is easy to find cos x = 4/5.
Using the Pythagorean triple 5, 12, 13 it is easy to find sin y = 12/13.
Thus, by substituting all the four values into the top equation, we get
csc(x+y)=1/ (3/5 ⋅ 5/13 + 4/5 ⋅ 12/13) = 65/63
Ques. Evaluate the following equation: (5 Marks)
sec(60) − csc(45)
Ans. On evaluating each term separately in the equation individually we get,
sec(60) = 1/cos(60)
=> 1/0.5
=> 2
csc(45) = 1/sin(45) = 1/(√2/2)
=> (2/√2)(√2/√2)
=> (2√2) / 2
=> √2
On equating the values of sec(60) and csc(45) in the given equation, we will get
sec(60) − csc(45)
=> 2 – (2√2)/2
=> 2 − √2
Ques. In a triangle, ABC is right-angled at B, length of side AB and AC is 5 and 10 cm respectively. Determine ∠ BAC and ∠ BCA. (5 Marks)
Ans.
According to the question, Δ ABC is right-angled at B
AB = 5 cm
AC = 10 cm

For calculating the value of ∠BCA:
In the given triangle, AC is the hypotenuse and AB is the opposite side.
Therefore, we will use sin ∠BCA
=> AB / AC
=> 5 / 10
= 1 / 2
We know sin 30° = ½
Therefore, sin ∠BCA = sin 30° or ∠ BCA = 30°
So, ∠BCA = 30°
For calculating the value of ∠BAC:
In any triangle, the sum of all interior angles is equivalent to 180° i.e.,
∠ABC + ∠BCA + ∠BAC = 180°
90° + 30° + ∠BAC = 180°
∠BAC = 60°
So, ∠BAC = 60°
Ques. Find the value of x in the equation given below: (5 Marks)
cosec 3x = (cot 30° + cot 60° / (1 + cot 30° cot 60°)
Ans. According to the question,
cosec 3x = (cot 30° + cot 60°) / (1 + cot 30° cot 60°) ……(1)
We know the values of
cot 30° = √3
cot 60° = 1/√13
On computing the above values in equation (1), we will get:
(cot 30° + cot 60°) / (1 + cot 30° cot 60°)
= (√3+1/√3) / (1+√3×1/√3)
= (3+1)/√3(3+1)2
= 4/√3 × ½
=> 2/√3
So, cosec 3x = 2/√3
We know that 2/√3 = cosec 60°
cosec 3x = cosec 60°
Therefore 3x = 60° or x = 20°
Hence value of x = 20°
Ques. Given an acute angle triangle ABC with value of sin (A + B - C)= 1/2, cot (A - B + C) = 0 and cos (B + C – A) =1/2. Determine the values of A, B, C? (5 Marks)
Ans. According to the question,
sin (A + B - C) = 1/2
cot (A - B + C) = 0
cos (B + C – A) =1/2
We know that value of sin 30° = ½
Given sin (A + B - C) = 12
=> A + B - C = 30° ......(1)
We know that value of cot 90°= 0
Given cot (A – B + C) = 0
=> A - B + C = 90° ......(2)
We know that value of cos 60° = 12
Given cos (B + C – A) = 12
=> B + C – A = 60° ......(3)
Solving the equations (1), (2), and (3) using elimination method
Adding the equation (1) and (2):
(A + B - C) + (A – B + C) = 30° + 90°
2A = 120°
Or A = 60°
Substituting the value A = 60° in equations (1) and (3) we get
(1) → 60° + B – C = 30° → B – C = - 30° ......(4)
(2) → B + C – 60° = 60° → B + C = 120° ......(5)
Adding equations (4) and (5)
(B - C) + (B + C ) = -30° + 120°
2B = 90°
∴ B = 45°
Substituting the value B = 45° in equation (4)
B – C = - 30°
45° – C = - 30° → C = 75°
Hence the required values are A = 60°, B = 45°and C = 75°
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments