
Collegedunia Team Content Curator
Content Curator
Relations and functions provide the relationship between any two entities.
- In our daily lives, we encounter various connections and patterns that describe relations, such as father-son relationships, brother-sister relationships, and so on.
- In mathematics, we see various number relationships, such as x is less than y, line l is parallel to line m, and so on.
- Relations and functions relate elements from one set (domain) to elements from another set (codomain).
- A relation R which is considered from a non-empty set B can be characterized as the subset of the cartesian product, A × B.
- The subset has been derived by depicting a relationship between the first and second element of the ordered pairs which are in A × B.
- A function can be expressed as a relation in math such that every element in the domain is related to one element in the codomain.
- Relations and functions can be illustrated in a variety of forms, like arrow representation, algebraic form, set-builder form, roster form, and tabular form.
- In this case, an ordered pair is represented as (INPUT, OUTPUT):
- A graph depicts the relationship between INPUT and OUTPUT. A function, on the other hand, is a relation that produces one OUTPUT for each INPUT.
- It is to be noted that all functions can be relations, but not all relations are functions.
Key Terms: Function, Linear Function, Onto Function, Cartesian Product, Identity Relation, Inverse Relation, Relations, Special Function, Ordered pair, Domanin, Codomain
What is a Function?
[Click Here for Sample Questions]
A function is a relation that states that each input should have only one output.
- A function is a special form of relation (a set of ordered pairs) that follows a law, i.e. any X-value should be associated with only one y-value.
- Functions can also be defined as special types of relations that define the correspondence between one quantity with another.
Relations and functions detailed explanation
For Example: In a relation, {(-2, 3), {4, 5), (6, -5), (-2, 3)}, we have:
| Domain | Range |
|---|---|
| -2 | -5 |
| 4 | 3 |
| 6 | 5 |
- Domain: It is a list of the ordered pair's first values (Set of all input (x) values).
- Range: It is a collection of the ordered pair's second values (Set of all output (y) values).
Thus, we can write the domain as {-2, 4, 6} and the range as {-5, 3, 5}.
Note: When writing the domain and range, don't take duplicates into account, and write them in ascending order.
Also Read:
Types of Functions
[Click Here for Previous Year Questions]
The types of functions can be described in terms of relations as follows:
- Injective function or one-to-one function: If there is a distinct element of Q for each element of P, the function f: P → Q is said to be one-to-one.
- Many to one function: Two or more elements of P are mapped to the same element of set Q by this function.
- Onto Function or Surjective function: A function for which every element of set Q has a pre-image in set P.
- One-to-one correspondence or Bijective function: Each element of P is matched with a discrete element of Q by the function f, and each element of Q has a pre-image in P.
Special Functions
The special functions include the following -
- Constant Function
- Linear Function
- Identity Function
- Absolute Value Function
- Inverse Functions
Read Also: Representation of a Function
What is Relation?
[Click Here for Sample Questions]
A subset of the cartesian product A × B is a relation R from a non-empty A to a non-empty set B.
- The subset is obtained by specifying a relationship between the first and second elements of the ordered pairs in A × B.
- In other words, the relationship between the two sets is known as the collection of the ordered pair, where the ordered pair is made up of objects from both sets.
- If two sets are assumed, the relation found between them can be established in case there is a connection between the elements of two or more than two non-empty sets.

Relation Representation
Example: (-2, 1), (4, 3), (7, -3), typically written with curly brackets in set notation type.
Also Read:
| Related Articles | ||
|---|---|---|
| Real-Valued Function | Polynomials Important Notes | Onto Function |
| Polynomial Important Questions | Binary Operations Important Notes | Symmetric and Skew Symmetric Matrices |
Types of Relations
[Click Here for Previous Years Questions]
The following are examples of various forms of relations:
- Empty Relations
- Universal Relations
- Identity Relations
- Inverse Relations
- Reflexive Relations
- Symmetric Relations
- Transitive Relations
Empty Relation
The relation R in A can be called an empty relation or void relation if no element of A bears any relation to any other element of A i.e.,
R = φ ⊂ A × A
For instance, suppose the fruit basket contains 100 mangoes.
- There is no way to find a relation R that will result in any apple being put in the basket.
- R is Void since it includes 100 mangoes but no apples.
Universal relation
R is a fixed relation; let's assume A is a universal relation since every element of A is connected to every element of A in this complete relation. R = A A, for example. i.e., R = A × A.
Every element of Set A is in Set B, so it's a complete relation.
Identity Relation
The Identity relation exists when any member of set A is only connected to only itself.
I={(A, A), ∈ a}.
For Example,
When we roll the dice, there are a total of 36 potential outcomes. i.e., (1, 1) (1, 2), (1, 3)…..(6, 6). The relation (1, 1), (2, 2), (3, 3) (4, 4) (5, 5) (6, 6) is an identity relation dependent on these.
Inverse Relation
If the components within each ordered pair are interchanged, then it results in the formation of an inverse relation i.e., R ∈ A X B. The relation R-1 = {(b,a):(a,b) ∈ R}.
For example, you throw two dice and if R = {(1, 2) (2, 3)} then R-1= {(2, 1) (3, 2)}.
Reflexive Relation
If every element of set A map to itself, i.e for every a ∈ A, (a, a) ∈ R is known as Reflexive Relation.
Symmetric Relation
In this case, if (a1,a2) ∈ R, this will mean that (a2, a2) ∈ R for all a1, a2 ∈ A.
Transitive Relation
For all a, b, c ∈ A, if (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R and this relation in set A is transitive.
Equivalence Relation
If a relation is reflexive, symmetric, and transitive then it is known as an Equivalence relation.
Representation of Relation and Functions
[Click Here for Sample Questions]
Relations and functions can be expressed in a variety of forms, including arrow representation, graph, algebraic form, set-builder form, roster form, and tabular form.
Example of Relation and Functions
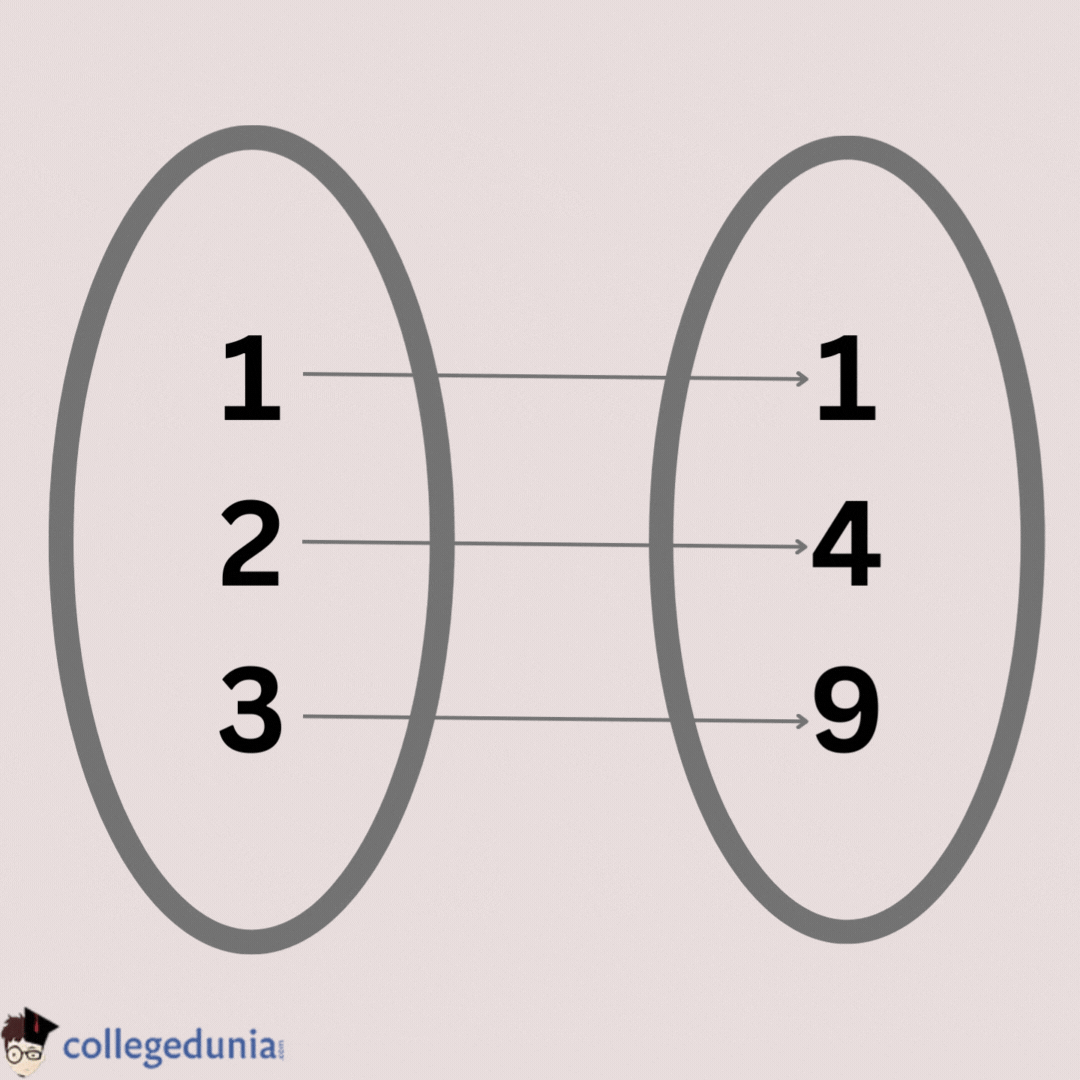
Express a function f: A = {1, 2, 3} → B = {1, 4, 9} such that f(1) = 1, f(2) = 4, f(3) = 9. Thus, it can be shown in different forms:
- Set-builder form: {(x, y): f(x) = y2, x ∈ A, y ∈ B}
- Roster form: {(1, 1), (2, 4), (3, 9)}
- Arrow Representation: It can be shown as:
Difference between Relation and Function
[Click Here for Previous Years Questions]
The differences between Relation and Function are:
| Relation | Function |
|---|---|
| A relation, in math, can be defined as a set of ordered pairs showing the relation between two sets. | A function can be defined as a relation where every element of the domain is related to a single element in the codomain. |
| A relation might or might not be a function. | All functions are relations. |
| For instance, {(1, x), (1, y), (4, z)}. | For instance, {(1, x), (6, y), (4, z)}. |
Important Topics for JEE MainAs per JEE Main 2024 Session 1, important topics included in the chapter relation and functions are as follows:
Some memory based important questions asked in JEE Main 2024 Session 1 include:
|
Things to Remember
- A Relation, in maths, is the relationship between two different sets of information.
- The types of relations are Empty Relations, Universal Relations, Identity Relations, Inverse Relations, Reflexive Relations, Symmetric Relations and Transitive Relations.
- Relations and functions can be represented in multiple forms, including Set-builder form, Roster form, Arrow Representation and more.
- A function is a relation in math where every element in the domain is related to one element in the codomain.
- The various types of functions are Injective function or one-to-one function, Many to one function, Onto Function or Surjective function and One-one correspondence or Bijective function.
Previous Year Questions
- The domain of the function f(x)=log2(x+3)x2+3x+2f(x)=log2(x+3)x2+3x+2 is...
- The number of functions that can be defined from the set A={a,b,c,d} into the set B={1,2,3} is equal to...
- Then 56∑n=1Δrf(n)∑n=156Δrf(n) is equal to...[JEE Main 2014]
- If NN is a set of natural numbers, then under binary operation...
- If FF is function such that F(0)=2,F(1)=3,F(x+2)=2F(x)−F(x+1)F(0)=2,F(1)=3,F(x+2)=2F(x)−F(x+1)...
- Satisfies the functional equation f(x−y)=f(x)f(y)−f(a−x)f(a+y)f(x−y)=f(x)f(y)−f(a−x)f(a+y)...
- The set {x:f(x)=f−1(x)}={1,2}{x:f(x)=f−1(x)}={1,2} f is a bijection and f−1(x)=1+√x−1,x≥1...
- If f:R→Sf:R→S defined by f(x)=sinx−√3cosx+f(x)=sinx−3cosx+ 1, is onto, function then S = ...?
- The graph of the function y=f(x)y=f(x)is symmetrical about the line x=2x=2, then…
- Let R={(1,3),(4,2),(2,4),(2,3),(3,1)} be a relation on the set A={1,2,3,4}. The relation R is...
Sample Questions
Ques. In mathematics, what are relations? (1 mark)
Ans. A relation is a mathematical concept that describes the relationship between two sets of ordered pairs of values. Domain refers to the set of elements in the first set, which is connected to the range, which refers to the set of elements in the second set.
Ques. Explain why addition, subtraction, multiplication and division are considered examples of binary operations? (1 mark)
Ans. In case of an addition, subtraction, multiplication and division only two numbers can be added, subtracted or multiplied at a time. If there is a third number, then we first multiply or add the first two numbers and then the result of the same is added or multiplied with the third. Hence these are considered as the examples of binary operations as binary means two.
Ques. What is meant by the composition of functions? (1 mark)
Ans. When two given functions for instance ‘a’ and ‘b’ are used to generate a third and new function ‘c’, it is known as composition of function. For instance, let's consider
f: A → B and g: B → C. Now we can denote the function of f and g as gof and define it as the function of gof: A → C. It can also be written as: gof (x) = g(f (x)), ∀ x ∈ A.
Ques. What is an example of equivalence relation? (1 mark)
Ans. If we throw two dice and keep a record of all its outcomes, we will notice that it shows all the properties of transitive, reflexive and symmetry relations. Thus, it can be considered as an example of an equivalence relation.
Ques. Express fog, assuming that f: R → R and g:R → R are represented by f(x) = |x| and g(x) = |5x – 2|. (Foreign 2011) (1 mark)
Ans. According to the question, f(x) = |x|, g(x) = |5x – 2|
∴ fog (x) = f[g(x)] = f{15x – 2|} = ||5x – 2||= |5x – 2| [∵ ||x|| = |x|]
Ques. Find out the range of function: ƒ(x) = \(\sqrt{}\)16 – x2. (3 marks)
Ans. The root value found inside can never be negative, which is why x2 should be less than 16.
This means x ∈ [-4,4]. It is known as the domain of the function.
For range, let y = \(\sqrt{}\)16 – x2
Which means, y2 = 16 – x2
or x2= 16 – y2
Now, because x ∈ [– 4, 4]
The Range of f = [0, 4].
Ques. Express a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1} and also find the domain, codomain and range of R. (4 marks)
Ans. As per the given question, A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.
Now, in order to find the range, the values of y for every value of x needs to determined, that is, when x = 1, 2, 3, 4, 5, 6, Thus:
x = 1, y = 1 + 1 = 2;
x = 2, y = 2 + 1 = 3;
x = 3, y = 3 + 1 = 4;
x = 4, y = 4 + 1 = 5;
x = 5, y = 5 + 1 = 6;
x = 6, y = 6 + 1 = 7.
Since 7 is not part of A, thus the relation R is defined on A.
Hence, range of R = (2,3,4,5,6)
Thus,
Domain = Codomain = (1,2,3,4,5,6),
Range = (2,3,4,5,6)
Ques. Show the function f: A—R. f(x) = x2 – 1. Consider A = { -4, 0, 1, 4) as a set of ordered pairs. (3 marks)
Ans. As per the question, it can be shown that:
A = {-4, 0, 1, 4}
f(x) = x2 – 1
f(-4) = (-4)2 – 1 = 16 – 1 = 15
f(0) = (0)2 – 1 = -1
f(1) = (1)2 – 1 = 0
f(4) = (4)2 – 1 = 16 – 1
= 15
Thus, the set of ordered pairs = {(-4, 15), (0, -1), (1, 0), (4, 15)}
Ques. Assume that f(x) = x2 and g(x) = 2x + 1 are two real functions. Determine (f + g) (x), (f –g) (x), (fg) (x), (f/g ) (x). (3 marks)
Ans. As given in the question, the two real functions are f(x) = x2 and g(x) = 2x + 1.
Thus,
(f + g) (x) = x2 + 2x + 1
(f – g) (x) = x2 -(2x + 1) = x2 – 2x – 1
(fg) (x) = x2(2x + 1) = 2x3 + x2
(f/g) (x) = x2/(2x + 1), x ≠ -½
Ques. Assume that R is the equivalence relation in a given set A = {0,1, 2, 3, 4, 5}, which is given by R = {(a, b) : 2 divides (a – b)}. Thus, express the equivalence class [0]. (2 marks)
Ans. As already give, R = {(a, b):2 divides(a – b)} and A = { 0,1, 2, 3, 4, 5}
Thus, [0] = {b ∈ A : (0, b) ∈ R}
= {b ∈ A: 2 divides (0 – b)}
= {b ∈ A : 2divides (-b)} = {0, 2, 4}
Therefore, the equivalence class of [0] is = {0, 2, 4}.
Ques. What is the difference between Relation and Function? (2 marks)
Ans. The difference between relations and functions is that relations specify any relationship between inputs and outputs, whereas functions create a relation with just one output for each input. Every function is a relation, but not every connection is a function.
Ques. What is the Range of Relation and Function? (2 marks)
Ans. The collection of all outputs from a relation or function is referred to as its range.
Check-Out:





Comments