Binary Operations: Types, Properties and Examples

Binary Operations are arithmetic operations such as addition, subtraction, division, and multiplication that are performed on two or more operands. Binary stands for two. In the case of more than two numbers, we first perform the given mathematical operation on two numbers and subsequently perform the other operations on its result. Thus, for any binary operation two inputs are required. 

Also Read: BODMAS Rule

Key Terms: Binary Operations, Arithmetic Operations, Addition, Subtrction, Multiplication, Division,  Closure Property, Non-Binary Operation, Functions, Relations

---

Binary Operations 

[Click Here for Sample Questions]

Binary operations are used to combine two elements of a package. We get a number when two numbers are inserted, subtracted, multiplied, or divided. Binary operations when performed on a set (consisting of operands) produces a third element from the same set. 

Binary operations include addition, subtraction, division, and exponential.

Let us consider a set of number son which binary operations is performed as A. The binary operations (addition, subtraction, multiplication or division) can be happen between the operands x and y of the set. Thus, the result of ^th eopertaion between x and y operands will be part of the same set A.  

Therefore, if the function is defined as * on a set A, then A*A = A. 

The operation performed on the elements can be written as x*y.

Also Read:

---

Types of Binary Operations

[Click Here for Previous Years Questions]

Binary operations that can be applied on operands are given below:

• Binary Addition
• Binary Subtraction
• Binary Multiplication
• Binary Division

Let us look at each of them in a little detail.

Binary Addition

Binary addition is applied to two binary numbers. The result is also a binary number. Following are some of the important rules:

• 0+0=0
• 0+1=1
• 1+0=1
• 1+1=10

Binary Addition Example

Binary Subtraction

Binary subtraction is applied on two binary numbers and the result hence obtained is also a binary number. Following are some important rules:

• 0-0=0
• 0-1=1 (with a borrow of 1)
• 1-0=1
• 1-1=0

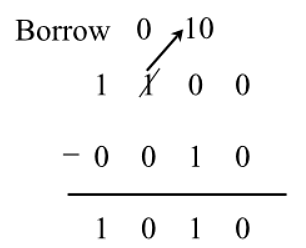
Binary Subtraction Example

Binary Multiplication

Two binary numbers can be multplied by the following rules:

• 0x0=0
• 0x1=0
• 1x0=0
• 1x1=1

Binary Multiplication Example

Binary Division

Binary division is similar to the 10 decimal system. The rules are as follows:

• 1 ÷ 1=0
• 1 ÷ 0=0
• 0 ÷ 1= meaningless
• 0 ÷ 0 = meaningless

Binary Division Example

---

Binary Operation Examples

[Click Here for Sample Questions]

For natural or real numbers, when we add two operands say p and q, the resultant will also be a natural or real number. 

Therefore, if R and N are real and natural numbers respectively, then,

+: R + R → R is derived by (p, q) → p + q

+: N + N → N is derived by (p, q) → p + q

This aapplies for other binary operations such as subtraction, multiplication, and division. 

Example

4-3

Here 4 and 3 are natural numbers. The resultant of 4-3 =1, is also a natural number obtained by the binary operation subtraction.

Similary,

(-5) X (-4)

Here, (-5) & (-4) are real numbers. The resultant of (-5) X (-4) = 20, is also a real number obtained by the binary operation multiplication. 

Read More: Multiplication & Division of Integers

---

Properties of Binary Operation 

[Click Here for Previous Years Questions]

Listed below are the important properties of binary operations.

Closure Property

Operation * with non-empty set A has closure property if  a ∈ P, b ∈ P ⇒ a * b ∈ P.

For example, addition is a binary operation closed on natural numbers, rational numbers, and integers.

Associative Property

For a non-empty set A with * as the binary operation, the following associative property holds true,

(a * b) *c = a*(b * c), where {a, b, c} ∈ A

Note: Subtraction denoted by ‘-’ is not associative .

Commutative Property

The binary operation * is commutative for a non-empty set A,

a * b = b * a, for all (a, b) ∈ A

For example, 4 and 6 are elements of the natural number set. 4+6 = 6+4= 10.

Distributive Property

Let $ and # be binary operation on a non-empty set A, then by distributive property

a$ (b # c) = (a $ b) # (a $ c), for all {a, b, c} ∈ A

For example, 4(3+5) = 4x3 + 4x5= 32

Identity Element

For a binary operation # on an non-empty set A,

e ∈A, if e#a = a#e= a, ∀ a ∈ A

where e is the identity element.

Inverse Property

If $ is a binary operation on a non-empty set A, 

a $ b = b $ a = e, ∀ {a, b, e}∈A

where a is the inverse of  and e is the identity element.

Read More: Cumulative Distribution Function

---

Binary Operation Table

[Click Here for Sample Questions]

Binary operation tables are visual representations of all the elements of a set and the binary operations being performed on them. Let us understand this with an example.

Consider a set A = {1,2,3,4,5}. The operation on the elements of set A is multiplication denoted by *.

Binary operation tables

From the table we can see that,

1*1 = 1

1*3 = 1

2*4 = 2

3*4 = 1

4*4 = 4

5*2 = 1 and so on. 

Elements and operation on the elements of the above set satify the closure, associative, ditributive, and commutative property of binary operations. 

Read More: Value of e

---

Things to Remember

• Binary operations on a set are calculations that combine two elements from the set (known as operands) to produce a third element from the same set. 
• The binary operations are not the additions on the set of all irrational numbers. 
• Multiplication of all irrational numbers is a non-binary operation.
• Some of the important properties of binary operations are : closure, associative, distributive, and associative. 
• Identity and inverse properties are also important in binary operations. 

Also Read:

---

Previous Year Questions on Binary Operations

1. If R is a relation on a set R of all real numbers defined by aRb, if |a-b| ≤ 1. Then R is? [BITSAT 2013]
2. Use binary multiplication to solve the function. [ KCET 2006]
3. Prove the associative and commutative property for the binary operations. [KCET 2006]
4. If A={a,b,c} then number of binary operations on A is? [KCET 2020]
5. In the group G={1,3,7,9} under multiplication, the inverse of 3 is? [KCET 2005]
6. In the group G={1,5,7,11}G={1,5,7,11} under multiplication modulo 1212, the solution of 7−1⊗12(x⊗1211)=57−1⊗12(x⊗1211)=5 is xx =...[KCET 2006]
7. In the group (Q+,⋆)(Q+,⋆) of positive rational numbers w.r.t. the binary operation ⋆⋆ defined by a⋆b=ab3,∀a,b∈Q+a⋆b=ab3,∀a,b∈Q+ the solution of the equation 5⋆x=4−15⋆x=4−1 in Q+Q+ is….[KCET 2005]
8. The image of the interval [-1, 3] under the mapping f:R→Rf:R→R given by f(x)=4x3−12xf(x)=4x3−12x is
9. (10101101)2=(................)10​
10. A binary sequence is an array of 0′s0′s and 1′s1′s. The number of nn -digit binary sequences which contain even number of 0′s0′s is​
11. The number of values of rr satisfying the equation 39C3r−1−39Cr2=39Cr2−1−39C3r39C3r−1−39Cr2=39Cr2−1−39C3r is​
12. On Q−{1}Q−{1} such that a∗b=a+b−aba∗b=a+b−ab. Find the identity element.​
13. Suppose that the number of elements in set AA is pp, the number of elements in set BB is qq and the number of elements in A×BA×B is 77. Then p2+q2=
14. The inverse of the function y=10x−10−x10x+10−xy=10x−10−x10x+10−x is equal to :​
15. The number of binary operations that can be defined on a set of 2 elements is​
16. The number of bijective function from a set A to itself when A contains 106 elements is​