Invertible Matrices: Theorems, Properties and Examples

Content Curator

Invertible Matrix, which is also called nonsingular or nondegenerate matrix, is a type of square matrix that contains real or complex numbers. We can say a square matrix to be invertible if and only if the determinant is not equal to zero. Meaning, a 2 × 2 matrix is only invertible if the determinant of the matrix is not 0 because if the determinant is zero, then the matrix is not invertible and has no inverse.

Table of Content

What is Invertible Matrix?
Properties of Invertible Matrix
Methods of Matrix Inversion
Things to Remember
Sample Questions

Key Terms: Invertible Matrix, Identity Matrix, Real numbers, Complex numbers, Determinant, Square matrix, Addition, Subtraction, Multiple, Division

What is Invertible Matrix?

[Click Here for Sample Questions]

Matrix is formed by an array of numbers that are arranged in rows and columns. The sum total of rows and columns stand for m and n respectively. The dimension of a matrix is given by m × n. All the mathematical Operations such as Addition, Subtraction, Multiple, and division can be done using a matrix. But here, we multiply the inverse of the matrix, for the purpose of Division. This inverse matrix is called the Invertible Matrix.

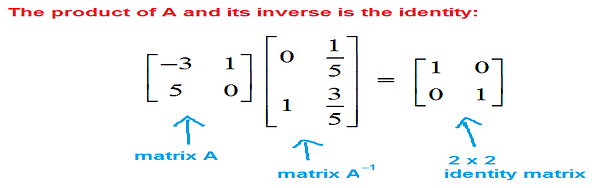
You must be well acquainted with the fact that when a number is multiplied with the inverse of that number, the result is One. Similarly, for the Matrix, when a matrix is multiplied with the inverse of that matrix, we get Identical Matrix.

The video below explains this:

Matrices Detailed Video Explanation:

Read More: Minors and Cofactors

Properties of Invertible Matrix

[Click Here for Sample Questions]

The properties of an Invertible Matrix A are listed below.

(A⁻¹)⁻¹ = A
(kA)⁻¹ = k⁻¹A⁻¹ for any nonzero scalar k
(Ax)⁺ = x⁺A⁻¹ if A has orthonormal columns, where + denotes the Moore–Penrose inverse and x is a vector
(A^T)⁻¹ = (A⁻¹)^T
For any invertible n × n matrices A and B, (AB)⁻¹ = B⁻¹A⁻¹. To be more specific, if A₁, A₂…, A_k is invertible n × n matrices, then (A₁A₂⋅⋅⋅A_k-1A_^k)⁻¹ = A⁻¹_kA⁻¹_k−1….A⁻¹₂A⁻¹₁
det A⁻¹ = (det A)⁻¹

Example: Suppose there are two squared Matrix A and B, where B is the inverse matric of A.

A = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\)

B = \(\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}\)

AB = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\) × \(\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}\)

= \(\begin{bmatrix} 4-3 & -6+6 \\ 2-2 & -3+4 \end{bmatrix}\) = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) = I

Also, BA = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) = I

Thus, B is the inverse of A, A = B⁻¹

Also Read:

Related Articles
Determinant of a Matrix	Properties of Determinants	Determinant Formula
NCERT Maths Chapter 3 Matrices Solutions	Orthogonal Matrix	Matrices
Matrices Important Questions	Transpose of a Matrix	Scalar Matrix
Symmetric Matrix	Identity Matrix	Matrices Handwritten Notes

Methods of Matrix Inversion

[Click Here for Sample Questions]

There are four methods of Matrix Inversion. They are:

Gaussian Elimination
Newton’s Method
Cayley- Hamilton Method
Eigen Decomposition Method.

There are two Theorems of Invertible Matrices. They are:

Theorem 1: (Uniqueness of inverse). If there exists an inverse of a matrix, it is unique.

We consider A = [ a_ij ] to be a square matrix of order m. Again we consider B and C to be two inverses of A. Now, we show that B = C.

As B is the inverse of A,

AB = BA = I ... (1)

And also, we have considered C is also the inverse of A

AC = CA = I ... (2)

Thus B = BI = B (AC) = (BA) C = IC = C

Theorem 2: If A and B are invertible matrices of the same order, then (AB) ^–1 = B^–1 A^–1

From the above definition of inverse of a matrix,

(AB) (AB)^–1 = I

or A^–1 (AB) (AB)^–1 = A^–1 I (Pre multiplying both sides by A^–1)

or (A^–1 A) B (AB)^–1 = A^–1 (Since A^–1 I = A^–1)

or IB (AB)^–1 = A^–1

or B (AB)^–1 = A^–1

or B^–1 B (AB)^–1 = B^–1 A^–1

or I (AB)^–1 = B^–1 A^–1

Hence (AB)^–1 = B^–1 A^–1

Read More: Singular Matrix

Things to Remember

Invertible Matrix, which is also called nonsingular or nondegenerate matrix, is a type of square matrix that contains real or complex numbers.
Matrix is formed by an array of numbers that are arranged in rows and columns.
The sum total of rows and columns stand for m and n respectively.
The dimension of a matrix is given by m × n.
All the mathematical Operations such as Addition, Subtraction, Multiple, and division can be done using a matrix.
But here, we multiply the inverse of the matrix, for the purpose of Division. This inverse matrix is called the Invertible Matrix.

Sample Questions

Ques. What is an identical Matrix? (2 Marks)

Ans. A matrix is called an Identity Matrix when the size of the matrix is n × n, where n is the row and column of the matrix. The n × n matrix has one on the main diagonal, and zeros elsewhere.

Ques. Does a rectangular Matrix possess an Inverse? (2 Marks)

Ans. A rectangular matrix does not possess an inverse matrix, since, for products BA and AB to be defined and to be equal, it is necessary that matrices A and B should be square matrices of the same order

Ques. What is the Application of Invertible Matrix? (2 Marks)

Ans. There is three application of Invertible Matrix, they are :

Least-squares or Regression
Simulations
MIMO Wireless Communications

Ques. When a square matrix is not invertible, what is it called? (2 Marks)

Ans. The square matrix which is not invertible is called singular or degenerate. When the value of the determinant of a square matrix is zero, that matrix is then called a singular matrix.

Ques. What are the properties of Matrix Inverse? (3 Marks)

Ans. If A and B are the non-singular matrices, then the inverse matrix should have the following properties:

(A^-1)^-1 =A
(AB)^-1 = A^-1B^-1
(ABC)^-1 = C^-1B^-1A^-1
(A₁ A₂….A_n)^-1 = A_n^-1A_n-1^-1……A₂^-1A₁^-1
(A^T)^-1 = (A^-1)^T
(kA)^-1 = (1/k)A^-1
AB = I_n, where A and B are inverse of each other.
If A is a square matrix where n>0, then (A^-1)ⁿ = A^-n
Where A^-n = (Aⁿ)^-1

Ques. What will be the value of ‘k’ if det(A^-1) = (det A)^k, if A is a 3 × 3 invertible matrix. (Delhi) (3 Marks)

Ans. We already know that,

A^-1 = Adj A / |A|

Therefore,

|A^-1| = |Adj A|/ |A|

= |A|^3-1/| A|

[ Since, if A is a non singular matrix of order n, then |adj (A)| = |A|^n-1]

= |A|²/ |A| = |A|

As we have |A^-1| = |A|^k Hence, k = 1.

Ques. If for any 2 × 2 square matrix A, A(adj A) = \(\begin{bmatrix} 8 & 0 \\ 0 & 8 \end{bmatrix}\) , then what will be the value of |A|. (All India) (3 Marks)

Ans. Solution 1,

Given, A (adj A) = \(\begin{bmatrix} 8 & 0 \\ 0 & 8 \end{bmatrix}\)

As we know that, A (adj A) = |A| – I

|A| . l = \(8 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

⇒ |A| = 8

Solution 2,

Given that, A(adj A) = \(\begin{bmatrix} 8 & 0 \\ 0 & 8 \end{bmatrix}\)

⇒ A (adj A) = \(8 \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

⇒ A(adj A) = 8I₂ …… (1)

As it is already known that for any square matrix A of order 2, we have

A (adj A) = |A| l₂ ….. (2)

From equation (1) and (2), we have,

|A| = 8.

Ques. By using elementary row transformation (ERT), find the inverse of matrix A = \(\begin{bmatrix} 6 & 5 \\ 5 & 4 \end{bmatrix}\). (Foreign 2010; HOTS) (5 Marks)

Ans. First of all, put A = IA, then convert this matrix in the form I = BA, by applying elementary row transformation on A of LHS and I of RHS where B gives the inverse of A.

As it is given, A = \(\begin{bmatrix} 6 & 5 \\ 5 & 4 \end{bmatrix}\)

Let us consider, A = IA

⇒ \(\begin{bmatrix} 6 & 5 \\ 5 & 4 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} A\)

By applying R₁ → R₁ – R₂, we get

\(\begin{bmatrix} 1 & 1 \\ 5 & 4 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix} A\)

Applying R₂ → R₂ – 5R₁, we get

\(\begin{bmatrix} 1 & 1 \\ 0 & -1 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ -5 & 6 \end{bmatrix} A\)

Applying R₁ → R₁ +R₂, we get

\(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} = \begin{bmatrix} -4 & 5 \\ -5 & 6 \end{bmatrix} A\)

Now, applying R₂ → (-1)R₂, we get

\(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} -4 & 5 \\ 5 & -6 \end{bmatrix} A\)

Hence,

A^-1 = \(\begin{bmatrix} -4 & 5 \\ 5 & -6 \end{bmatrix}\) [∵ A^-1A = I]

Ques. Using elementary row transformation, find inverse of matrix A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\) (Delhi 2010) (3 Marks)

Ans. Given,

A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\)

We can write,

A = IA

i.e.,

\(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} A\)

\(\begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix} A \quad\left[R_{1} \rightarrow R_{1}-R_{2}\right]\)

\(\begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 \\ -1 & 2 \end{bmatrix} A \quad\left[R_{2} \rightarrow R_{2}-R_{1}\right]\)

\(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix} A \quad \left[R_{1} \rightarrow R_{1}-2 R_{2}\right]\)

\(\therefore \quad A^{-1} = \begin{bmatrix} 3 & -5 \\ -1 & 2 \end{bmatrix}\)

Ques. Find the inverse of the matrix \(\begin{bmatrix} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}\). (Delhi 2012) (5 Marks)

Ans. The given matrix is, A = \(\begin{bmatrix} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix}\)

Let us assume, A = IA

⇒ \(\begin{bmatrix} -1 & 1 & 2 \\ 1 & 2 & 3 \\ 3 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₂ → R₂ + R₁, R₃ → R₃ + 3R₁, we get

\(\begin{bmatrix} -1 & 1 & 2 \\ 0 & 3 & 5 \\ 0 & 4 & 7 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{bmatrix} A\)

And applying R₁ → (-1) R₁, we get

\(\begin{bmatrix} 1 & -1 & -2 \\ 0 & 3 & 5 \\ 0 & 4 & 7 \end{bmatrix} = \begin{bmatrix} -1 & 0 & 0 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{bmatrix} A\)

Applying R₂ → R₂ – R₃, we get

\(\begin{bmatrix} 1 & -1 & -2 \\ 0 & -1 & -2 \\ 0 & 4 & 7 \end{bmatrix} = \begin{bmatrix} -1 & 0 & 0 \\ -2 & 1 & -1 \\ 3 & 0 & 1 \end{bmatrix} A\)

Applying R₁ → R₁ – R₂ and R₃ → R₃ + 4R₂, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & -1 & -2 \\ 0 & 0 & -1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 1 \\ -2 & 1 & -1 \\ -5 & 4 & -3 \end{bmatrix} A\)

Applying R₂ → (-1)R₂, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 2 \\ 0 & 0 & -1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 1 \\ 2 & -1 & 1 \\ -5 & 4 & -3 \end{bmatrix} A\)

Applying R₂ → R₂ + 2R₃, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 1 \\ -8 & 7 & -5 \\ -5 & 4 & -3 \end{bmatrix} A\)

Applying R₃ → (-1)R₃, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & -1 & 1 \\ -8 & 7 & -5 \\ 5 & -4 & 3 \end{bmatrix} A\)

which is of the form I = BA

Hence,

A^-1 = \( \begin{bmatrix} 1 & -1 & 1 \\ -8 & 7 & -5 \\ 5 & -4 & 3 \end{bmatrix}\)

Ques. Find the inverse of the matrix \(\begin{bmatrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}\). (Foreign 2011) (5 Marks)

Ans. The given matrix is A = \(\begin{bmatrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}\)

Let A = IA

⇒ \(\begin{bmatrix} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₁ → 3R₁, we get

\(\begin{bmatrix} 6 & 0 & -3 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix} = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₁ → R₁ – R₂, we get

\(\begin{bmatrix} 1 & -1 & -3 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}=\begin{bmatrix} 3 & -1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₁ → R₁ + R₃, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}=\begin{bmatrix} 3 & -1 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₂ → R₂ – 5R₁, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 3 \end{bmatrix}=\begin{bmatrix} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 0 & 0 & 1 \end{bmatrix} A\)

Applying R₃ → R₃ – R₂, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix}=\begin{bmatrix} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 15 & -6 & 6 \end{bmatrix} A\)

Applying R₃ → \(\frac{1}{3}\)R₃, we get

\(\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{bmatrix} A\)

Hence,

\(A^{-1}=\begin{bmatrix}3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2\end{bmatrix}\)

For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates

Check-Out:

Class 11 & 12 PCMB Study Guides
NCERT Solutions for Class 12 Physics	Class 12 Physics Notes	Formulas in Physics
Topics for Comparison in Physics	Choice-based questions in physics	Topics in relation to physics
Physics Study Notes	Class 12 Physics Book PDF	Class 12 Physics Practicals
Important Derivations in Physics	SI units in Physics	Important Physics Constants and Units
Class 12 Physics Syllabus	Mendeleev's Periodic Table	NCERT Solutions for Class 12 Biology
NCERT Solutions for Class 12 English	NCERT Solutions for Class 11 Chemistry	Class 12 Chemistry Practicals
Class 12 Chemistry Notes	Important Chemical Reactions	Class 12 Maths Notes
Class 12 PCMB Notes	NCERT Class 12 Biology Book	NCERT Class 12 Maths Book
NCERT Class 12 Textbooks	NCERT Solutions for Class 11 Maths	NCERT Solutions for Class 11 Physics
NCERT Solutions for Class 12 Maths	NCERT Solutions for Class 11 Biology	NCERT Solutions for Class 11 English
NCERT Class 11 Chemistry Book	NCERT Class 11 Physics Book	NCERT Class 11 Biology Book
Class 11 Notes	Important Maths Formulas	Important Chemistry Formulas
Class 11 PCMB Syllabus	Chemistry Study Notes	Biology Study Notes
Periodic Table in Chemistry	Important Chemical Reactions	Comparison topics in Chemistry
Comparison Topics in Maths	Biology MCQs	Important Named Reactions
Maths MCQs	Comparison Topics in Biology	Chemistry MCQs

Invertible Matrices: Theorems, Properties and Examples

What is Invertible Matrix?

Matrices Detailed Video Explanation:

Properties of Invertible Matrix

Methods of Matrix Inversion

Things to Remember

Sample Questions

CBSE CLASS XII Related Questions

1.
Let A=\(\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\),show that(aI+bA)ⁿ=aⁿI+na^n-1bA,where I is the identity matrix of order 2 and n∈N

2.
Find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)

3.
For what values of x,\(\begin{bmatrix} 1 & 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 & 0\\ 2 & 0 & 1 \\1&0&2 \end{bmatrix}\)\(\begin{bmatrix} 0 \\2\\x\end{bmatrix}\)=O?

4.
Find the vector and the cartesian equations of the lines that pass through the origin and(5,-2,3).

5.
Evaluate \(\begin{vmatrix} cos\alpha cos\beta &cos\alpha sin\beta &-sin\alpha \\ -sin\beta&cos\beta &0 \\ sin\alpha cos\beta&sin\alpha\sin\beta &cos\alpha \end{vmatrix}\)

6.
Find the following integral: \(\int (ax^2+bx+c)dx\)

Comments

SUBSCRIBE TO OUR NEWS LETTER

Invertible Matrices: Theorems, Properties and Examples

What is Invertible Matrix?

Matrices Detailed Video Explanation:

Properties of Invertible Matrix

Methods of Matrix Inversion

Things to Remember

Sample Questions

CBSE CLASS XII Related Questions

1. Let A=\(\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\),show that(aI+bA)n=anI+nan-1bA,where I is the identity matrix of order 2 and n∈N

2. Find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)

3. For what values of x,\(\begin{bmatrix} 1 & 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 & 0\\ 2 & 0 & 1 \\1&0&2 \end{bmatrix}\)\(\begin{bmatrix} 0 \\2\\x\end{bmatrix}\)=O?

4. Find the vector and the cartesian equations of the lines that pass through the origin and(5,-2,3).

5. Evaluate \(\begin{vmatrix} cos\alpha cos\beta &cos\alpha sin\beta &-sin\alpha \\ -sin\beta&cos\beta &0 \\ sin\alpha cos\beta&sin\alpha\sin\beta &cos\alpha \end{vmatrix}\)

6. Find the following integral: \(\int (ax^2+bx+c)dx\)

Comments

SUBSCRIBE TO OUR NEWS LETTER

1.
Let A=\(\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\),show that(aI+bA)ⁿ=aⁿI+na^n-1bA,where I is the identity matrix of order 2 and n∈N

2.
Find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\)

3.
For what values of x,\(\begin{bmatrix} 1 & 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 & 0\\ 2 & 0 & 1 \\1&0&2 \end{bmatrix}\)\(\begin{bmatrix} 0 \\2\\x\end{bmatrix}\)=O?

4.
Find the vector and the cartesian equations of the lines that pass through the origin and(5,-2,3).

5.
Evaluate \(\begin{vmatrix} cos\alpha cos\beta &cos\alpha sin\beta &-sin\alpha \\ -sin\beta&cos\beta &0 \\ sin\alpha cos\beta&sin\alpha\sin\beta &cos\alpha \end{vmatrix}\)

6.
Find the following integral: \(\int (ax^2+bx+c)dx\)