
Collegedunia Team Content Curator
Content Curator
The diagonal of a cube formula is \(\begin{array}{l}\sqrt{3}x\end{array}\). The diagonal of a cube helps calculate the lengths of the diagonals (which are the face diagonals and the body diagonals). The diagonal of a cube is the line segment which connects two non-adjacent cube vertices. It can be derived by using the Pythagoras Theorem. Cubes are solid three-dimensional figures with 6 square faces, 12 edges, and eight vertices.
A cube is said to be a regular hexahedron. In geometry, the length, breadth and height of a cube are all equal, which makes the figure symmetrical in shape. It is usually represented in an XYZ plane. The faces of a cube are in a squared shape with equal dimensions. The angles of a cube are found to be at a right angle. And, the opposite edges of a cube are parallel to one another.
| Table of Content |
Key Terms: Cube, Symmetry, Square, Diagonal, Right-angle, Vertex, Sides, Height, Three-Dimensional Geometry
What is a Cube?
[Click Here for Sample Questions]
A cube is a regular hexahedron which has 6 square faces, 12 edges and eight vertices. Cubes are three-dimensional solid shapes which have equal length, width, and height with each face as a square.
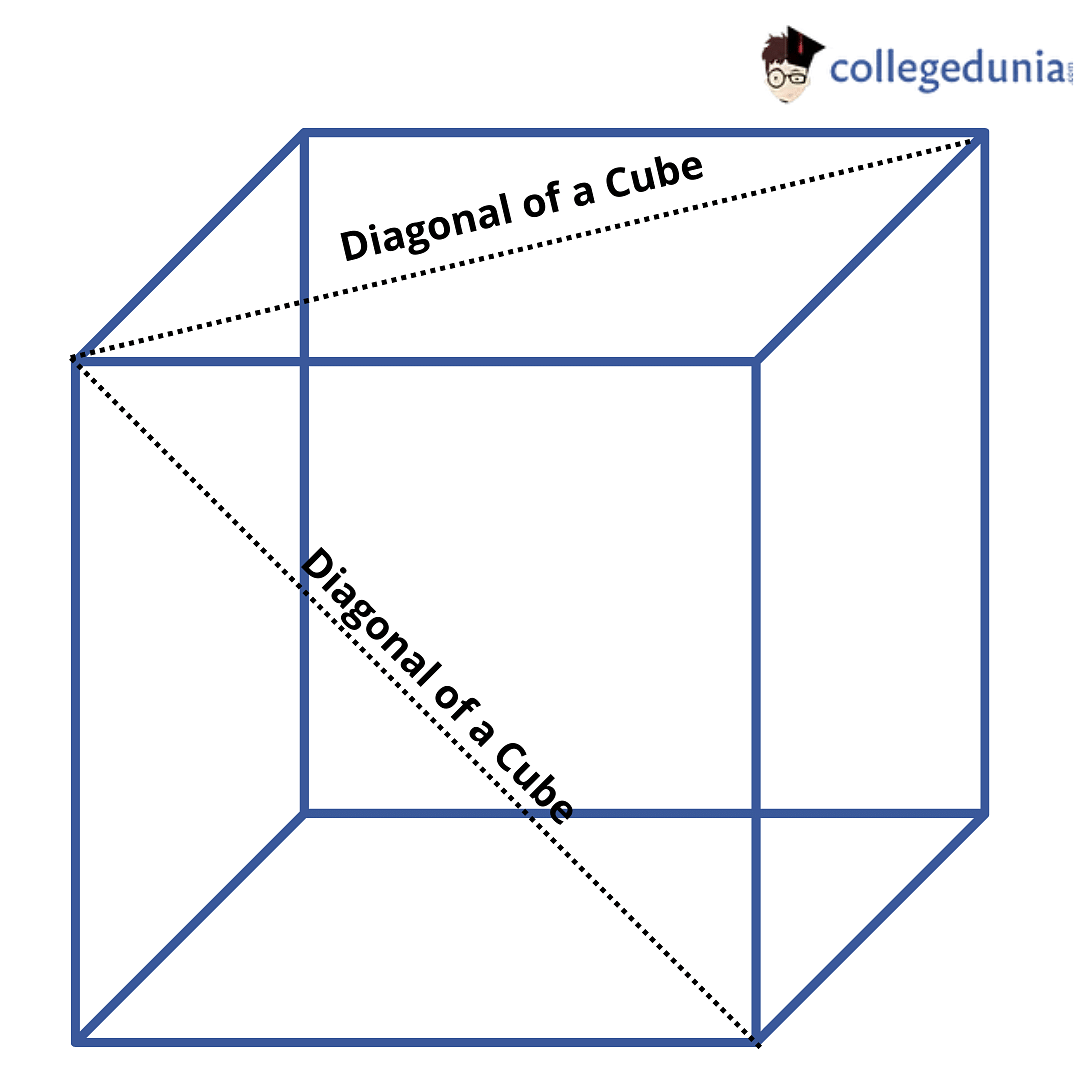
Diagonal of a Cube
The diagonal of a cube, as can be seen from the above image as well, cuts via the centre of the cube. However, the diagonal of a face of a cube is not considered the main diagonal. Typically, the main diagonal of a cube can be determined by the help of multiplying the length of one side with the square root of 3.
What is Diagonal of a Cube?
[Click Here for Sample Questions]
The diagonal of a cube can be defined as a line segment, in the cube, which connects any two non-adjacent vertices. There are mainly two types of diagonals in a cube because it is in three-dimension:
Face Diagonal of a Cube
In Face-Diagonal, a cube has 6 square-shaped faces with 2 diagonals on either face that joins the non-adjacent vertices. Thus, a cube has 12 face diagonals.
Body Diagonal of a Cube
Body diagonals typically connect the opposite vertices of a cube which pass via the body of the cube. Thus, a cube here has 4 body diagonals which pass via the cube connecting the opposite corners.
Read Also:
Diagonal of a Cube Formula
[Click Here for Sample Questions]
The Diagonal of a Cube Formula can be denoted by:
| Diagonal of a Cube = \(\begin{array}{l}\sqrt{3}x\end{array}\) |
The primary diagonal of a Cube cuts through the centre of the Cube; the diagonal of the Cube's face is not the main diagonal. The main diagonal of a cube can be determined by the help of multiplying the length of one side with the square root of 3 (it is also called the body diagonal of a cube).
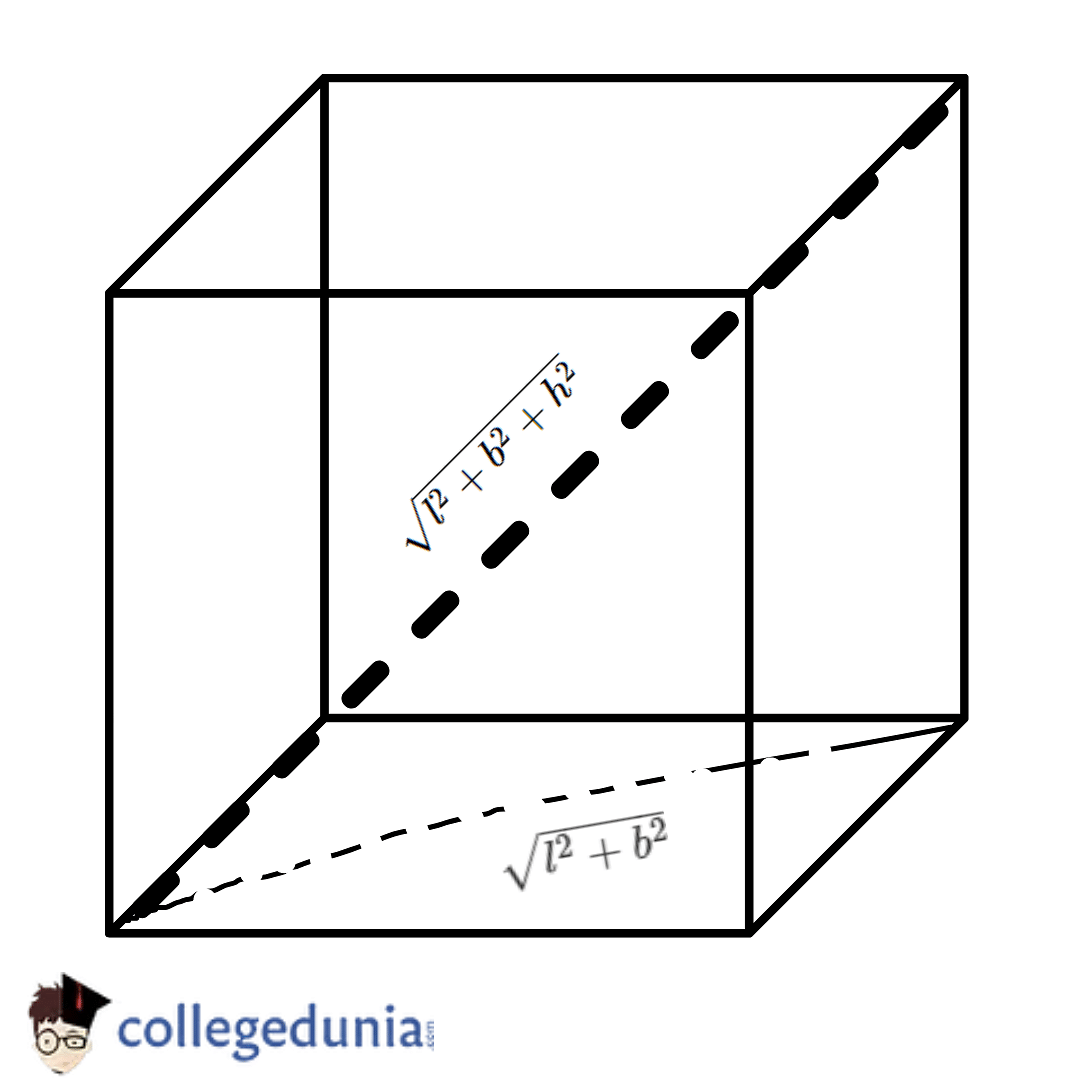
Diagonal of a Cube
Diagonal of a Cube Derivation
With the help of Pythagoras theorem, we get a2 + r2 = d2 (… equation 1)
Now, we are aware that the face diagonal is √2a so, 'r' can be substituted by √2a, meaning 'r' = √2a
By replacing the value of r in equation 1,
⇒ a2 + (√2a)2 = d2
⇒ a2 + 2a2 = d2
⇒ 3a2 = d2
⇒ d = √(3a2)
⇒ d = √3a
Hence, the diagonal of a cube formula is = √3a
| Example: Determine the length of body diagonal of a cube assuming its side length is 7 inches. Ans: As per the given question Side length of the cube (a) = 7 inches To determine: Body diagonal Length of each body diagonal of cube = √3a After substitution, Length of body diagonal of cube = √3a ⇒ √3a ⇒√3 × 7 = 12.12 inches. Hence, the length of the body diagonal is considered 12.12 inches. Example: Determine the face diagonal of a cube if its side length is 5 m. Ans: As per the question, a = 5 Now, after using the given formula, we get, d =\(\sqrt{2}a\) ⇒ \(\sqrt{2} \ (5)\) ⇒ (1.414)(5) ⇒ 7.07 m |
Properties of a Cube
[Click Here for Sample Questions]
There are several properties of a cube. Some of them are:
- A Cube has 6 faces in square shape.
- The dimensions of the faces and sides of a cube are equal.
- All the angles in a Cube are at right angle.
- Any face of a cube meets the other four at each of the edges.
- The vertex of a Cube has three edges and three faces.
- Opposite edges of a Cube are parallel to one another.
Things to Remember
- The diagonal of a cube formula is \(\begin{array}{l}\sqrt{3}x\end{array}\).
- The diagonal of a cube calculates the lengths of the diagonals (Simply, face diagonals and the body diagonals).
- Cubes are known as solid three-dimensional figures that has 6 square faces, 12 edges, and eight vertices.
- There are two diagonals of a cube, Face Diagonal of a Cube and Body Diagonal of a Cube.
Sample Questions
Ques. What is the diagonal of a cube that has the given side of 10 cm? [3 marks]
Ans. As per the question, the given side is, x = 10 cm
We are aware that the diagonal of a cube is \(\sqrt{3x}\)
Thus, the diagonal of a cube will be = \(\sqrt{3} (10)\)
The value of \(\sqrt{3} \) = 1.734
Thus, the diagonal of a cube = 1.734 \(\times\) (10)
So, the diagonal of a cube is = 17.34 cm.
Ques. Determine the diagonal of the cube with side of 5 cm. [3 marks]
Ans. The given side, x = 5 cm
Now, by using the diagonal formula, we have
Diagonal of cube = \(\begin{array}{l}\sqrt{3}x\end{array} \)
Thus, after replacing the values, we get
Diagonal of cube =\(\begin{array}{l}\sqrt{3}x\end{array} \)\(\times\)5
It is known that the value of √3 is 1.734
Hence, the diagonal of a cube = 1.734 (5)
Thus, the Diagonal of the cube is = 8.67 cm
Ques. The body diagonal of a cube’s length is given as 8√3 units. Determine the length of each side of the cube. [2 marks]
Ans. As per the given question, body diagonal = 8√3 units
According to the formula, the length of the body diagonal of a cube = √3a
So, upon substitution,
Length of body diagonal of a cube = √3a
⇒ 8√3 = √3a
⇒ a = 8
Ques. What is the formula to determine the diagonal of a cube? [1 mark]
Ans. The formula to compute the length of the body diagonal or the main diagonal of a cube can be expressed by = √3a (here, a = Length of each side of a cube).
Ques. The length of the diagonal of a cube has been mentioned as \(9 \sqrt{3}\) Units. Determine the length of each side. [2 marks]
\(9 \sqrt{3}\) = √3a \(\times\) a
⇒ a = \(\frac{9 \sqrt{3}}{\sqrt {3}}\)
⇒ a = 9 Units
Ques. List some properties of a cube. [3 marks]
Ans. Some properties of a cube are:
- Any face of a cube meets the other four at each of the edges.
- The vertex of a Cube has three edges and three faces.
- Opposite edges of a Cube are parallel to one another.
Ques. Are the diagonals of a cube equal? [2 marks]
Read More:







Comments