
Collegedunia Team Content Curator
Content Curator
Area of segment of a circle is obtained through subtracting the area of the triangle from the area of the sector. A line segment that joins two points on a circle or curve with both the end points lying on the arc is called a Chord. The region of the circle cut off from the rest of the circle by this chord is called as segment of a circle. This segment is a part of a circle in two dimensional space bounded by a chord whose end points lie on the arc. In other words, the segments can be defined as the parts that are divided by the circle's arc and connected with the chord through its end points.
| Table of Content |
Keyterms: Circle, Traingle, Line segment, Chord, Major segment, Minor segment, Radians, Degree
Also Read: Surface Areas and Volumes
Types of Segments in a Circle
[Click Here for Sample Questions]
The segments of a circle can be classified into two types that are Major segment and Minor segment. When the chord divides the regions of a circle into segments, the segment that has larger area is known as a major segment and the segment that has smaller area is known as Minor segment.
The major segment consists of a major arc and the minor segment consists of a minor arc. Here it can be observed that ADC is the major segment and ABC is the minor segment. Besides, the area of these segments of a circle can also be calculated using formulas.

Types of Segments in a Circle
Also, read: Areas Related to Circles Revision Notes
Area of Segment of a Circle: Formula
[Click Here for Sample Questions]
The formula that can be used to calculate the area of segments of a circle is as follows. It can be calculated either in terms of degree or radian.
- Area of Segment in Radians: A= (½) × r^2 (θ – Sin θ)
- Area of Segment in Degree: A= (½) × r^ 2 × [(π/180) θ – sin θ]
Derivation
Let us consider a circle which has a triangle AOB circumscribed within.
Let ∠AOB = θ°
And area of triangle AOB is AΔAOB
Then the Area of sector AOBC = θ/360° × πr2 (Formula).
So, the area of Segment of Circle can be calculated as
Area of Segment = Area of Sector – Area of Triangle

Sector of a Circle
A = θ/360° × πr2 – A ΔAOB
To find the area of triangle AOB we need to calculate the sides.
Using Pythagoras theorem
OP =\({\sqrt{[r^2 -(\frac{AB}{2}) 2]}}\) in case the length of AB is given.
Or OP= rcos(θ/2) in case the angle θ is given.
Area of triangle= ½ × Base × Height
= ½ × AB × OP.
In this way the area of Segment of a circle can be calculated by substituting the given values.
Area of Segment in Degree: A= (½) × r^ 2 × [(π/180) θ – sin θ]
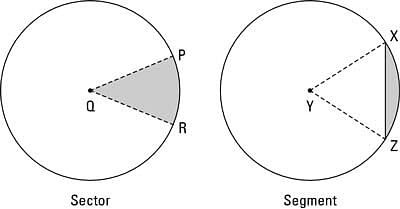
Sector vs Segment of a Circle
Also Read:
| Related Articles | ||
|---|---|---|
| Semicircles | Tangent to a Circle | Areas Related to Circles |
| Perimeter and Area of a Circle | Circumference of Circle | Area of a Triangle |
Theorems on Segment of Circle
[Click Here for Sample Questions]
There are two theorems on segments of a circle.
Alternate Segment Theorem
The theorem states that in a circle, the angle which lies between the chord and tangent passing through the end points is equal to the angle in the alternate segment.
Add image
Here the angle lying between the tangent DE and chord BC is ∠BCE and the angle in alternate segment is ∠BAC.
According to the theorem, ∠BCE = ∠BAC.
Another angle lying between tangent DE and chord AC is ∠ACD and the angle in alternate segment is ∠ABC.
According to the theorem, ∠ACD = ∠ABC.
Angle in the same Segment Theorem
The theorem states that the angles formed in a segment are all equal i.e., angles in the same segment of a circle are equal.
According to the theorem, ∠PAQ = ∠PBQ.
From the inscribed angle Theorem, it can be inferred that an angle formed by an arc at the center of a circle is double the angle divided by the same arc at any other point in the circle.
Therefore, ∠POQ = 2∠PAQ
∠POQ = 2∠PBQ.
From these two we can conclude that
2∠PAQ= 2∠PBQ
Hence, ∠PAQ = ∠PBQ
Read more Important Questions on Circles
Things to Remember
- The region of the circle cut off from the rest of the circle by this chord is called a Segment of a circle.
- It is a part of a circle in two dimensional space bounded by a chord that has its end points lying on the arc.
- There are two types of Segments: Major segment and Minor segment.
- The segment that has a larger area is called the Major segment and the segment that has smaller area is called the minor segment.
- The formula that can be used to calculate Area of Segment in Degree: A= (½) × r^ 2 × [(π/180) θ – sin θ]
- There are two theorems on Segment of Circle that are Alternate segment theorem and Angle in the same segment theorem.
- Alternate Segment Theorem states that in a circle, the angle which lies between the chord and tangent passing through the end points is equal to the angle in the alternate segment.
- Angle in the same segment Theorem states that the angles formed in a segment are all equal i.e., angles in the same segment of a circle are equal.
Also, read: Circles Revision Notes
Sample Questions
Ques. Calculate the area of the major segment of a circle if the area of its minor segment is 54sq. units and the radius is 7units. Use π=22/7. (2 Marks)
Ans. From the formula
area of the major segment = area of the circle − the area of the minor segment
=πr^2−54
=22/7×7×7−62
=92sq.units
Ques. PQ is a chord of a circle that subtends an angle of 90° at the center of a circle, and the diameter of the circle is 14cm. Calculate the area of the minor sector of this circle? (2 Marks)
Ans. The diameter of the circle =14 cm.
The radius of circle =14/2=7 cm
Using the formula of the area of a sector of the circle
The area of minor sector =(θ/360?)×πr^2=(90°/360°)×(22/7)×7^2=11×7/2=38.5sq.cm.
Therefore, the area of the minor sector is 38.5sq⋅cm.
Ques. If the area of a sector is 80 sq.cm and the area of the enclosed triangle is 68sq.cm, calculate the area of the segment? (2 Marks)
Ans. From the formula
Area of the segment = area of the sector – area of the triangle
=(80−68)sq.cm
=12sq.cm
Thus, the area of the segment is 12sq.cm.
Ques. What is the difference between Sector and Segment of a circle? (3 Marks)
Ans. The sector and segment are both parts of a circle. A segment is bound by the circumference of the circle and chord. The sector is bound by the circumference of a circle and two radii. Radius of the circle is important and considered in the sector. But the radius is not much considered for the segment.
If the chord is double the radius of a circle, the segments of a circle can be equal and referred to as semicircles. If the angle between two radii is 180° the sectors can be referred to as semicircles.
Ques. Calculate the area of a segment of a circle with a central angle of 165 degrees and a radius of 4. Express answer to nearest integer. (3 Marks)
Ans. From the formula
Area of the segment = area of the sector – area of the triangle
Area of sector = n/360 × πr^2
= 165/360 × π4^2
= 23.02 sq.cm
Area of triangle = ½ × B × H
= ½ × 2\({\sqrt{}}\)3 × 2
= 3.46 sq.cm
Area of Segment = 23.02 – 3.46
= 20 sq.cm
Ques. Explain the formula of area of Segment of Circle with derivation. (5 Marks)
Ans. The formula used to calculate the area of Segment of a circle is
Area of Segment in Radians: A= (½) × r^2 (θ – Sin θ)
Derivation:
Let us consider a circle which has a triangle AOB circumscribed within.
Let ∠AOB = θ°
And area of triangle AOB is AΔAOB
Then the Area of sector AOBC = θ/360° × πr2 (Formula).
So, the area of Segment of Circle can be calculated as
Area of Segment = Area of Sector – Area of Triangle
A = θ/360° × πr2 – AΔAOB
To find the area of triangle AOB we need to calculate the sides.
Using Pythagoras theorem
OP = \({\sqrt{[r^2 -(\frac{AB}{2}) 2]}}\) incase the length of AB is given.
Or OP= rcos(θ/2) incase the angle θ is given.
Area of triangle= ½ × Base × Height
= ½ × AB × OP.
In this way the area of Segment of a circle can be calculated by substituting the given values.
Area of Segment in Degree: A= (½) × r^ 2 × [(π/180) θ – sin θ]
Check-Out:







Comments