
Content Curator
Annulus is a ring-shaped geometric figure or, more broadly, a term used to designate a ring-shaped object in mathematics. It is also known as the space between two concentric rings. It is similar to the right-hand throw-ring. A round disc with a circular hole is another example. The ring's outer and inner rings are concentric circles (circles that share a common centre point with different radius).
| Table of Content |
Keyterms: Annulus, Circle, radius, circumference, centre, plane, set, ring
What is an Annulus?
[Click Here for Sample Questions]
A circle is a curve sketched out by a point moving in a plane so that its distance from a given point is constant. Alternatively, it is the shape formed by all points in a plane that are at a set distance from a given point, the centre. A planar figure bordered by the circumference of two concentric circles of two distinct radii is known as an annulus.
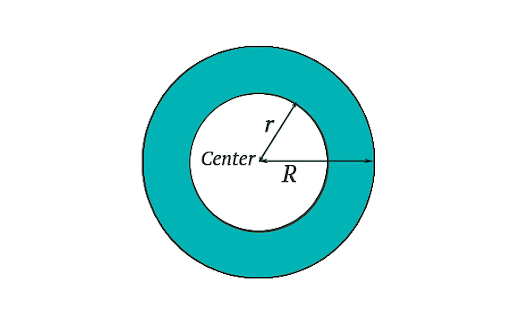
Annulus
The two radii R, r in the diagram, which are the radii of the outer ring and the inner 'hole,' respectively, determine the dimensions of an annulus. In the figure shown, the shaded portion, representing a ring, is known as the annulus. Individually, we have 2 circles, with a radii R and r, where R>r.
Also Read:
| Related Articles | ||
|---|---|---|
| Tangent to a Circle | Areas Related to Circle | Perimeter and area of a circle |
| Real Numbers | Real Numbers formula | Distance formula |
Annulus Formula
[Click Here for Sample Questions]
A two-dimensional shape's perimeter is defined as the route or border that encircles it and the size of the region encompassed inside any 2D form is its area. By the definition of Annulus, we know that it is a 2D figure, therefore, the area and perimeter of Annulus are:
Perimeter = 2π (R + r)
Area: A = π (R2 – r2)
Area of Annulus
[Click Here for Sample Questions]
The area of an annulus is equal to the difference between the areas of the bigger R-radius circle and the smaller r-radius circle.

Area of the annulus
Let A be the area of the outer circle and 'a' be the area of the smaller circle. Thus, the area of Annulus is:
Area = A - a
We know that the area of a circle is
A= πr2
Thus the difference between the areas of two concentric circles having radius R and r is given by,
A = πR2 – πr2
→ A = π (R2 – r2)
Read More: Important Questions on Circle
The length of the longest line segment within an annulus, which is the chord tangent to the inner circle, 2d in the accompanying diagram, determines the annulus' area.

Longest line in the annulus
Since this line is parallel to the smaller circle and perpendicular to its radius at that point, d and r are sides of a right-angled triangle with hypotenuse R, and the area of the annulus is determined by the Pythagorean theorem.
A = π (R2 – r2) = πd2
Perimeter of Annulus
[Click Here for Sample Questions]
The annulus's perimeter equals the sum of the radii of the large and small circles multiplied by 2 pi. Given that, a radius of the outer circle is R and that of the inner circle is r, therefore by definition,
Perimeter of Annulus = 2πR + 2πr = 2π (R + r)
Things to Remember
- An annulus is a flat ring-like form. Its edges are made up of two circles with the same centre.
- A spherical shell is a three-dimensional version of an annulus in geometry. It's the space between two concentric circles with different radii that a ball occupies.
- An annulus is certainly something you've seen in your daily life. The colourful rings on an archery target or the face of a CD are two examples of things that create a set of annuli.
- The area of an annulus is given by, A = π (R2 – r2)
- The perimeter of an annulus is given by, 2π (R + r)
Also Read:
Sample Questions
Ques. If the area of an annulus is 1092 inches and its width is 3 cm, then find the radii of the inner and outer circles? (2 marks)
Ans. Let the inner radius of an annulus be r and its outer radius be R.
Then width = R – r
3 = R – r
R = 3 + r
We know,
Area of the annulus = π (R2 – r2)
or
Area of the annulus = π (R + r) (R – r)
1092 = 22/7 (3 + r + r) (3)
3 + 2r = 1092×722×3
3 + 2r = 115.82
2r = 115.82 – 3
2r = 112.82
r = 56.41
R = 3 + 56.41
= 59.41
So, Inner radius = 56.41 inches
Outer radius = 59.41 inches
Ques. A steel pipe has an outside diameter (OD) of 100mm and an inside diameter (ID) of 80mm, what is the area of the cross-section? (2 marks)
Ans. Convert diameter to radius for both outside and inside circles:
R = 100 mm / 2 = 50 mm
r = 80 mm / 2 = 40 mm
Now calculate area:
Area = π (R2 – r2)
Area = 3.14 × ( 502 − 402 )
Area = 3.14× (2500 − 1600)
Area = 3.14 × 900
Area = 2827 mm2 (to nearest mm2)
Ques. If the inner radius is 4 cm and the outer radius is 5 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 5cm
r = 4cm
Area = 22/7 (52 - 42 )
Area = 28.26 sq.cm
Ques. If the inner radius is 9 cm and the outer radius is 10 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 10cm
r = 9cm
Area = 22/7 (102 - 92 )
Area = 59.66 sq.cm
Ques. If the inner radius is 16 cm and the outer radius is 18 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 18cm
r = 16cm
Area = 22/7 (182 - 162 )
Area = 213.52 sq.cm
Ques. If the inner radius is 23cm and the outer radius is 28 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 28cm
r = 23cm
Area = 22/7 (282 - 232 )
Area = 800.7sq.cm
Ques. If the inner radius is 50 cm and the outer radius is 56 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 56cm
r = 50cm
Area = 22/7 (562 - 502 )
Area = 1997.04 sq.cm
Ques. If the inner radius is 44 cm and the outer radius is 50 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 50cm
r = 44cm
Area = 22/7 (502 - 442 )
Area = 1770.96 sq.cm
Ques. If the inner radius is 102 cm and the outer radius is 110 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 110cm
r = 102cm
Area = 22/7 (1102 - 1022 )
Area = 5325.44 sq.cm
Ques. If the inner radius is 17 cm and the outer radius is 36 cm, find the area of the annulus. (2 marks)
Ans. Area = π(R2 - r2)
R = 36 cm
r = 17 cm
Area = 22/7 (362 - 172 )
Area = 3161.98 sq.cm
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments