
Content Writer
Quadratic Equations are algebraic expressions of degree 2 in one variable and are of the form ax2 + bx + c = 0. In simpler terms, a quadratic equation is be defined as a polynomial equation of degree 2. The general form of a quadratic equation is ax2 + bx + c = 0, where, x denotes the variable, a and b are the numerical coefficients, c is the constant term and a ≠ 0.
The values of the variable x that satisfy the quadratic equation are called the roots of the quadratic equation. There are a maximum of two roots of a quadratic equation and are designated as (α, β).
Key Terms: Quadratic Equations, Degree, Quadratic Formula, Discriminant, Degree, Roots, Zeroes, Variable, Factorization
What are Quadratic Equations?
[Click Here for Sample Questions]
Quadratic Equations are defined as polynomial equations with degree 2 in one variable. The general form of a quadratic equation is given as:
ax2 + bx + c = 0
Where
- x denotes the variable.
- a and b are the numerical coefficients and a ≠ 0.
- c is the constant/absolute term.
The values that fulfil a given quadratic equation are called roots of the quadratic equation and each equation has a maximum of 2 roots. The roots may be real or imaginary. When a quadratic polynomial is equivalent to zero it will become a quadratic equation.
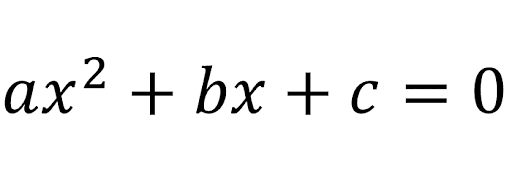
Standard Form of Quadratic Equation
The video below explains this:
Quadratic Equations Detailed Video Explanation:
Read More: Quadratic Equations MCQ
Roots of a Quadratic Equation
[Click Here for Previous Years Questions]
The roots of a quadratic equation are those two values of the variable that satisfy a quadratic equation. The roots of a quadratic equation are also referred to as zeroes of the equation and are designated as (α, β). The roots can be both real or imaginary where the real roots of an equation are the coordinate points at which it intersects the x and y-axis, respectively.
If f(a) = 0 then a is a root of f(x).
- If a = c, roots are reciprocals of each other.
- If b = c = 0, roots are zero.
- If c = 0, one of the roots is zero, and the opposite one will be = -b/a.
Example: The roots of a quadratic equation x2 - 3x - 4 = 0 are (-1,4) as both of them satisfy the equation.
- When x = -1, (-1)2 - 3(-1) - 4 = 1 + 3 - 4 = 0
- When x = 4, (4)2 - 3(4) - 4 = 16 - 12 - 4 = 0
The roots of a quadratic equation can be calculated using various methods, of which the quadratic formula is the easiest one.
Quadratic Formula
[Click Here for Sample Questions]
Quadratic Formula is one of the easiest ways to find the roots of a quadratic equation. The roots or zeroes of a quadratic equation ax2 + bx + c = 0 are given by the quadratic formula which is as follows:
(α, β) = [-b ± √(b2 – 4ac)]/2a
The (+) and the (-) sign can be alternatively used to obtain the two distinct roots of the quadratic equation.
Solved ExampleExample: Find out the roots of the quadratic equation x2 - 3x - 4 = 0 using the quadratic formula. Solution: In the given quadratic equation, a = 1, b = -3, and c = -4 Using the Quadratic Formula, x = [-b ± √(b2 - 4ac)]/2a Thus, x = 4 and x = -1 are the roots of the quadratic equation x2 - 3x - 4 = 0. |
Important Formulas for Solving Quadratic Equations
[Click Here for Previous Years Questions]
Here is a list of important formulas that are used to solve the quadratic equations in a simple and easy manner:
- The roots of the quadratic equation: x = (-b ± √D)/2a, in which D = b2 – 4ac
- Nature of the Roots
- D > zero, roots are real and distinct (unequal)
- D = 0, roots are real and equal (coincident)
- D < 0, roots are imaginary and unequal
- The roots (α + iβ), (α – iβ) are conjugate pairs of each other.
- Sum and Product of Roots: If α and β are the roots of a quadratic equation, then
- S = α+β= -b/a = coefficient of x/coefficient of x2
- P = αβ = c/a = constant term/coefficient of x2
- The quadratic equation in the form of roots: x2 - (α + β)x + (αβ) = 0
- The quadratic equations a1x2 + b1x + c1 = 0 and a2 x2 + b2x + c2 = 0 have:
- One common root if (b1c2 – b2c1)/ (c1a2 – c2a1) = (c1a2 – c2a1)/(a1b2 – a2b1)
- Both roots common if a1/a2 = b1/b2 = c1/c2
- In quadratic equation ax2 + bx + c = 0 or [(x + b/2a)2 – D/4a2]
- If a > zero, minimal value = 4ac – b2/4a at x = -b/2a.
- If a < 0, maximum value = 4ac – b2/4a at x= -b/2a.
- If α, β, γ are roots of cubic equation ax3 + bx2 + cx + d = 0, then, α + β + γ = -b/a, αβ + βγ + λα = c/a, and αβγ = -d/a
- A quadratic equation will become an identity (a, b, c = zero) if the equation is solved by using more than two numbers, that is, having extra than two roots either real or complicated.
Discriminant of a Quadratic Equation
[Click Here for Sample Questions]
In a quadratic equation, the term (b2 – 4ac) represents the discriminant of a given quadratic equation. The discriminant helps us to reveal the nature of roots.
- If the value of discriminant (d) = zero i.e., b2 – 4ac = 0, the quadratic equation will have same roots i.e., α = β = -b/2a
- If d < 0 i.e., b2 – 4ac < 0, the quadratic equation will have imaginary roots i.e., α = (p + iq) and β = (p – iq).
- If (D) > zero i.e., b2 – 4ac > zero, the quadratic equation will possess real roots.
- If the value of d > zero and is a perfect square, the quadratic equation will possess rational roots.
- If the value of (d) > 0 and d is not a perfect square, the quadratic equation will possess irrational roots i.e. α = (p + √q) and β=(p – √q).
- If the value of d> 0, d is a perfect square, a = 1, and b and c are integers, the quadratic equation will have integral roots.
Methods to Solve Quadratic Equations
[Click Here for Previous Years Questions]
There are two roots or zeroes of a quadratic equation. We can find the roots of a quadratic equation with the help of four different methods which are as follows.
- Using Quadratic Formula
- Factorization
- Completing the Square Method
- Graphing Method
Each of these methods has been explained in detail below.
Using Quadratic Formula
The quadratic formula is used to calculate the roots of a quadratic equation immediately from the general form. It is easy to effortlessly replace the values from the given equation on this system and calculate the roots. The (+) & (-) signs imply that there are two roots of the equation.
Solved ExampleExample: Calculate the roots of the equation x2-5x+6 = 0 by using the quadratic formula. Solution: On comparing the given equation with the general form ax2+bx+c = 0 a = 1, b = -5 and c = 6 b2-4ac = -52-4×1×6 = 1 Roots of the given equation:
Thus, 3 and 2 are the roots of the quadratic equation x2-5x+6 = 0. |
Factorization
In factorization of the quadratic equation, we need to follow a sequence of steps. First, we need to split the middle term into two terms in such a manner that the product of the terms is equal to the constant term. Lastly, the common terms is taken out from the available term, to finally obtain the factors.
Solved ExampleExample: Consider a quadratic equation 2x2−5x+ 3= 0 ⇒2x2−2x−3x+3= 0 This step is splitting the centre term
2x2−2x−3x+3=0 2x(x−1)−3(x−1)=0 (x−1)(2x−3)=0 Therefore, 1 and 3/2 are the roots of the given equation. |
Read More: Complex Numbers & Quadratic Equations Important Questions
Completing the Square Method
Completing the square method involves algebraically squaring and simplifying the quadratic equation to obtain the required roots.
In order to determine the roots of the quadratic equation ax2 + bx + c = 0, we need to first simplify it
- ax2 + bx + c = 0
- ax2 + bx = -c
- x2 + bx/a = -c/a
Next, express the left-hand side as a perfect square, by adding a new term (b/2a)2 on both sides:
- x2 + bx/a + (b/2a)2 = -c/a + (b/2a)2
- (x + b/2a)2 = -c/a + b2/4a2
- (x + b/2a)2 = (b2 - 4ac)/4a2
- x + b/2a = +√(b2- 4ac)/2a
- x = - b/2a +√(b2- 4ac)/2a
On simplifying the equation further and taking the square root, the two roots are x = (-b + √(b2- 4ac))/2a. The '+' and '-' sign gives both the roots of the quadratic equation.
Completing the square method is quite detailed and lengthy and is generally avoided.
Graphing Method
The graphical method can be understood with the help of the given example:
Solved ExampleExample: Aftab tells his daughter, “seven years ago, I was seven times as old as you were then. Additionally, three years from now, I will be three times as old as you will be.” This represents this example algebraically and graphically. Solution: Let the present age of Aftab = x The present age of his daughter is represented as = y Seven years in the past, Aftab’s age = x – 7 Age of Aftab's daughter = y – 7 Based on the question, (x – 7) = 7 (y – 7 ) x – 7 = 7 y – 49 x – 7y = – 49 + 7 x – 7y = – 42 … (i) x = 7y – 42 Placing y = 5, 6, and 7, we get x = 7 × 5 – 42 = 35 – 42 = – 7 x = 7 × 6 – 42 = 42 – 42 = 0 x = 7 × 7 – 42 = 49 – 42 = 7 3 years from now, Aftab’s age = x + 3 Age of Aftab's daughter = y + 3 According to the question, (x + 3) = 3 (y + 3) x + 3 = 3y + 9 x – 3y = 9 – 3 x – 3y = 6 … (ii) x = 3y + 6 With the setting, y = – 2, –1, and 0, we get x = 3 × – 2 + 6 = – 6 + 6 =0 x = 3 × – 1 + 6 = – 3 + 6 = 3 x = 3 × 0 + 6 = zero + 6 = 6 Algebraic representation From equations (i) and (ii) x – 7y = – 42 … (i) x – 3y = 6 … (ii) By solving and substituting values for x, we can obtain values of y and obtain numerous points which can be plotted on the coordinate axis to obtain a parabola-shaped graph for the quadratic equation. The point(s) where the graph intersects the x-axis is the solution of the quadratic equation. We can also obtain the points algebraically by equalizing the y value to 0 in the function y = ax2 + bx + c and solving for x. |

Graphical Method to Solve Quadratic Equations
Tips and Tricks for Solving Quadratic Equations
[Click Here for Sample Questions]
Here are a few tips and tricks to solve quadratic equations in a simpler and easier manner.
- Generally, we solve the quadratic equations through factorization, however, we use the quadratic formula when it cannot be solved by factorization.
- Quadratic equations that have negative discriminant values, their roots are represented by complex numbers.
- The sum and product of roots of a quadratic equation are to be utilized in order to find higher algebraic expressions involving these roots.
Applications of Quadratic Equations
[Click Here for Previous Years Questions]
Quadratic Equation plays an essential role to solve many problems in real life as well as in subjects like physics, mathematics, etc. If we know what is the use of quadratic equations in real life, then this topic becomes more interesting to study. Following are the uses of quadratic equations in different places.
- Quadratic Equations are used to calculate the areas of a room, box, park, furniture, land, etc.
- Use to Calculate parallel resistance in Physics.
- Designing the shape of satellite dishes.
- Use in sports when we throw objects in the air to calculate speed.
- To solve parabolic equations.
Things to Remember
- A quadratic equation is a polynomial equation of degree 2 in one variable.
- The general form of a quadratic equation is ax2 + bx + c = 0 where a and b are the coefficients, c is the constant term and a ≠ 0.
- The roots of a quadratic equation are the values of x satisfying the quadratic equation. There are only two roots or zeroes of a quadratic equation which may be either real or imaginary.
- There are mainly four ways to calculate the roots of a quadratic equation namely Using Quadratic Formula, Factorization, Completing the Square Method and Graphing Method.
- The quadratic formula is the easiest way to find the roots of an equation and is given as x = [-b ± √(b2 - 4ac)]/2a.
Previous Years’ Questions
- If one root of the quadratic equation ax2 + bx + c = 0 is equal to… (BITSAT 2007)
- The product of all values of (cosα +isinα)3/5 is equal to… (VITEEE 2007)
- If one root is square of the other root of the equation…
- The common roots of the equations…
- Let a, b, and c be real numbers such that a +b + c <0… (WBJEE 2019)
- If the roots of the equation x2 + ax + b = 0… (VITEEE 2011)
- The smallest positive integer n for which… (KCET 2004)
- Suppose that two persons A and B solve the equation… (KEAM)
- If α and β are the roots of the equation…
- If b2≥4ac for the equation ax4+bx2+c=0, then all the roots…
Sample Questions
Ques. A car travels 20 km at a uniform speed. The speed of the train is increased by 10 km/hr, it takes 4 minutes less to cover the same distance. Find the initial speed of the train. [5 Marks]
Ans. Let the initial speed of the car be x km/hr
Therefore, New speed = ( x+10) km/hr
Time taken by car to cover 20 km = Distance/time
= (20 km)/(x km/hr)
= (20/x)hrs
New Time to cover the same distance after increasing the speed,
20/(x+10) hrs
From the given condition,
20/(x+10) = 20/x - 4/60 hrs
By Solving. We get
X2 + 10x - 3000 = 0
X2 + 50x - 60x - 3000 = 0
( x - 60 ) ( x + 50 ) = 0
On Solving We get,
X = 60, X = - 50
But speed will never be negative, so the speed will be 60 km/ hr.
Ques. The three sides of a right-angled triangle are X, X+2 and 10. Find x and then the area, if the longest side is 10. [5 Marks]
Ans. The longest side will be the hypotenuse. Therefore, we can write:
X2 + (X+2)2 = 102
On Solving,
2X2 + 4X - 96 = 0
X2 + 2x - 48 = 0 (Divide the complete equation by 2)
By factorization Method,
X2 + (8 - 6)x - 48 = 0
X2 + 8x - 6x - 48 = 0
x(x + 8) - 6(x + 8) = 0
(x + 8) (x - 6) = 0
(x + 8) = 0 or (x - 6) = 0
x = -8 or x = 6
We can only take x = 6 here because the length can’t be negative.
Here, x = 6 and therefore, Area = (½) x 6 x 8 = 24
Ques. Find the root of equation by factorization X2 + 3X - 18 = 0 [3 Marks]
Ans. Let us first split the middle terms 3X as 6X, -3X [Because (6x) x (-3x) = -18 X2 = X2 x -18].
So,
X2 + 3X - 18 = 0
X2 + 6X - 3X - 18 = 0
X( X + 6 ) - 3( X + 6 ) = 0
( X + 6 ) ( X - 3) = 0
Now X2 + 3X - 18 = 0 this can be written as ( X + 6 ) ( X - 3) = 0
So, the values of x for which X2 + 3X - 18 = 0 are the same for which ( X + 6 ) ( X - 3) = 0,
I.e., either x + 6 = 0 or x - 3 = 0.
Now, x + 6 = 0 gives x = - 6 & x - 3 = 0 gives x = 3.
So, x = - 6 & x = 3 are the solutions of the equation.
Ques. Find the values of x for which the expression (x2 – 4x + 3)/(x2 + x + 1) ≤ zero. [2 Marks]
Ans. Let f(x) = x2 – 4x + 3 and g(x) = x2 + x + 1.
The coefficient of x2 in g(x) is effective and the fee of discriminant (d) < zero. As a result, g(x) is advantageous for all values of x.
Due to the fact, f(x)/g(x) < 0. Therefore, f (x) ought to be much less than 0.
i.e. x2 – 4x + 3 < zero
Or, (x – 3) (x – 1) < zero
Therefore, 1 < x < 3.
Ques. The quadratic equations x2 – ax + b = 0 and x2 – px + q = zero have a commonplace root and the second equation has equal roots, displaying that b + q = ap/2. [3 Marks]
Ans. With the aid of thinking about α and β to be the roots of equation (i) and α to be the common root, we can clear up the problem via the use of the sum and fabricated from the roots system.
The given quadratic equations are
x2 – ax + b = zero ………. (i)
x2 – px + q = 0 ………..(ii)
From equation (i), α + β = a, α = b
From equation (ii), 2α = p, α2 = q
b + q = αβ + α2 = α (α + β) = ap/2
Ques. Determine the values of m for which the quadratic equations 3x2 + 4mx + 2 = 0 and 2x2 + 3x – 2 = 0 may have a not unusual root. [2 Marks]
Then, 3α2 + 4mα + 2 = 0 and 2α2 + 3α – 2 = zero
With the usage of the go multiplication method, we've
(-6 – 4)2 = (9 – 8m) (-8m – 6)
⇒ 50 = (8m – 9)(4m + 3)
Or, 32m2 – 12m – 77 = 0
Or, (8m + 11) (4m – 7) = 0
Consequently, the values of m for which the given quadratic equations could have common roots = -11/8 and 7/4.
Ques. Find the quadratic equation having the roots 3 and 4 respectively. [2 Marks]
Ans. The quadratic equation having the roots α, β, is x2 - (α + β)x + αβ = 0.
Given α = 3, and β = 4.
Therefore the quadratic equation is:
x2 - (3 + 4)x + 3×4 = 0
x2 - 7x + 12 = 0
Hence, the required quadratic equation is x2 - 7x + 12 = 0
Ques. Solve for x: x²+10x-11 = 0 [2 Marks]
Ans. Let us express 10x as a sum of 10x and 1x.
x2+11x-x-11 = 0
x(x+11)-1(x+11) = 0
(x+11)(x-1) = 0
x-11 = 0 or x+1 = 0
x = 11 or x = -1
Ques. Solve x2 – 6 x = 16. [2 Marks]
Ans. x2 – 6 x = 16 becomes x2 – 6 x – 16 = 0
x2-8x+2x-16 = 0
x(x-8)+2(x-8) = 0
(x+2)(x-8) = 0
x+2 = 0 or x-8 = 0
x = -2 or x = 8
Ques. The quadratic equation 5x2 + 8x + 12 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β. [2 Marks]
Ans. The quadratic equation having roots that are reciprocal to the roots of the equation aX2 + bx + c = 0, is cX2 + bx + a = 0.
The given quadratic equation is 5x2 + 8x + 12 = 0. Hence, the required equation having reciprocal roots is 12 X2 + 8x + 5 = 0.
Therefore, the equation is 12 X2 + 8x + 5 = 0.
Ques. There is a rectangular park. The length of the rectangular base is more than its breadth by 2m and the diagonal is more than the length of 1 m. Find the length and breadth of the park. [5 Marks]
Ans. Let the breadth of the rectangular park be X m.
Therefore, length = ( X + 2 ) m
Diagonal = (( X + 2 ) + 1) m
= (X + 3) m
It becomes Right Angled triangle, so by Pythagoras theorem it becomes
(X+2)2 + X2 = (X + 3)2
X2 + 2X + 4 + X2 = X2 + 6X + 9
After solving the equation it becomes,
X2 - 4X - 5 = 0
X2 - (5 - 1)X - 5 = 0
X2 - 5X + X - 5 = 0
X (X - 5) + 1 (X - 5) = 0
(X - 5) (X + 1) = 0
X - 5 = 0 or X + 1 = 0
So, the value of x is either 5 or -1. We have to reject -1 because length can’t be negative.
So, the width of the park is 5 and the length of the park is 7.
Ques: If 1 is a root of the equations of ay2 + ay + 3 = 0 and y2 + y + b = 0, then what will be the value of ab? [2 Marks]
Ans. ay2 + ay + 3 = 0
a (1)2 + a (1)2 + 3 = 0
2a = -3
a = -3/2
y2 + y + b = 0
(1) + (1) + b = 0
b = -2
Therefore, ab = (-3/2) (-2) = 3
Ques. Solve the following quadratic equation for x: x2 - 2ax - (4b2 - a2) = 0 [2 Marks]
Ans. The quadratic equation can be written as x2 - 2ax - (4b2 - a2) = 0
Or, x2 - 2ax - 4b2 + a2 = 0
Or, x2 - 2ax + a2 - 4b2 = 0
Or, (x - a)2 - (2b)2 = 0
As we know,
a2 - b2 = (a + b) (a - b)
(x - a + 2b) (x - a - 2b) = 0
Or, x - a + 2b = 0
Or, x - a - 2b = 0
Therefore, x = a - 2b or, a + 2b





Comments