
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Area under the curve is defined as the area of the region enclosed by the curve line and the coordinate axis.The area under the curve can be calculated using the equation of the curve, boundaries of the curve, and the axis enclosing the curve. Since the area under the curve is not a fixed shape, there is no definite formula for calculating it. To calculate the area under the curve, the integration method is used to solve the equation.
| Table of Content |
Key Takeaways: Area under the Curve, Integration, Circle, Parabola, Area between two Curves, Area between Curve and a Line
Read Also: Fundamental Theorem of Calculus
Methods for Calculating Area Under the Curve
[Click Here for Sample Questions]
There are different methods for calculating area under the curve. Out of them, the antiderivative method is mainly used. For calculating the area under the curve, the equation of the curve, limits across which area is to be calculated and the axis enclosing the area should be known. To calculate the area under the curve, first we need to find the integration (antiderivative) of the curve and then apply upper and lower limits to the integral. Finally, by taking their difference, the area under the curve can be calculated.
Area under the curve = a ∫b y.dx
Area under the curve = a ∫b f(x).dx
Area under the curve = [g(x)]ab = g(b) - g(a)
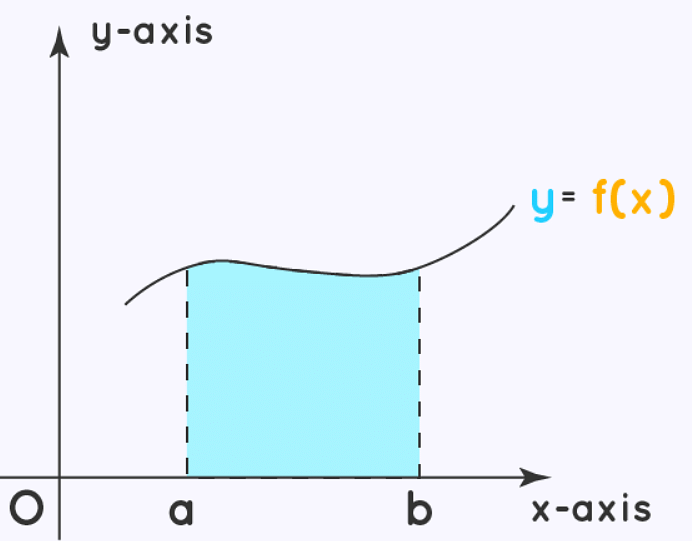
Area under the curve
Below are the two different methods used to calculate the area under the curve:
- By breaking the total region under the curve into smaller rectangles - In this method, the area under the curve can be calculated by dividing the total area into small rectangles. The upper limit for the number of rectangles is taken infinity (\(\infty\)). Finding the summation of the area of these rectangles provides the total area under the curve.
- Its formula can be written as: A = lim\( \)\(x\rightarrow\infty\) \( \sum^n_n-1\)f(x).x
- By the process of integration - To use this method, the equation of the curve, axis enclosing the area and the upper and lower limit values are required.
For a curve having an equation y = f(x) and limits as a and b, the formula for area under the curve can be written as: a ∫b f(x).dx
Read Also: Trigonometry Table
Area under the curve Detailed Video Explanation:
Formula for Area Under the Curve
[Click Here for Sample Questions]
There are different formulas for calculating area under the curve with respect to different axes enclosing the area. These are:
- Area with respect to the x-axis
In this case, the area is enclosed between the curve and the x-axis as shown below:
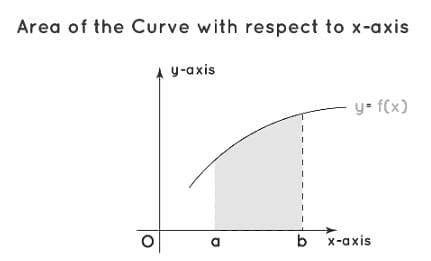
Area with respect to the x-axis
Here, the equation of the curve is y = f(x) and the formula for area under the curve is given by;
A = a ∫b f(x).dx
- Area with Respect to y-axis
In this case, the area is enclosed between the curve and the y-axis as shown below:
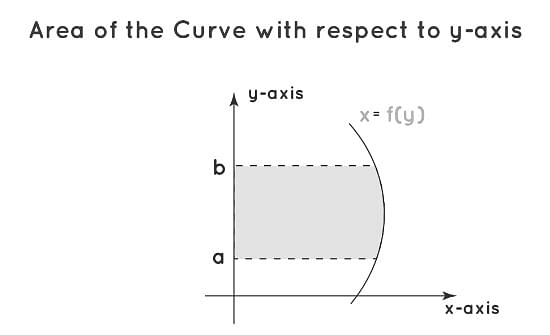
Area with Respect to y-axis
Here, the equation of the curve is x = f(y) and the formula for area under the curve is given by;
A = a ∫b f(x).dx
Also Read:
| Related Articles | ||
|---|---|---|
| Applications of Derivatives | Integration by Parts | Integers As Exponents |
- Area Below the axis
The value of the area under the curve below the axis is a negative value. So, we need to take the modulus of the area.

Area Below the axis
Here, the equation of the curve is y = f(x) and the formula for calculating the area under the curve is given by;
A = I a ∫b f(x).dx I
Read Also: Increasing and Decreasing Functions in Calculus
- Area Above and Below Axis
In some cases, the area enclosed by the curve is partially below the axis and partially above the axis. In such cases, the area of both the regions (i.e. above and below the axis) is calculated separately. The total area is given by the sum of the two areas. Since the value of the area of the portion below the axis is a negative value, we need to take its modulus.

Area Above and Below Axis
Here, the total area of the curve is given by adding areas A1 and A2;
A = IA1I + A2
A = I a ∫bf(x).dx I + a ∫\( \int\limits_b^c\)b f(x).dx
Also Read: Differential Equations
Different Cases for Calculating Area Under Curve
[Click Here for Sample Questions]
For different shapes like circle, parabola etc., area can be calculated using the concept of area under the curve.
- Area of a Circle
A whole circle can be divided into four quadrants. The area of a circle is four times the area of one of its quadrants. The area of the quadrant of a circle can be calculated by the method of integration used for calculating area under the curve.

Area of a Circle
The equation of the curve is y = (a2 - x2) and the limit is from O to a.
A = 4Oa y.dx
= 4Oa (a2 - x2).dx
= 4 [x/2 (a2 - x2) + a2/2 Sin-1x/a]aO
= 4 [((a/2) O + (a2/2) Sin-11) - 0]
= 4 (a2/2) (/2)
= a2
Hence, the area of the circle is given by a2.
- Area of a Parabola
An axis through the parabola divides it into two symmetric parts. By calculating the area under the curve of one part of the parabola and doubling it, the total area of the parabola can be calculated.
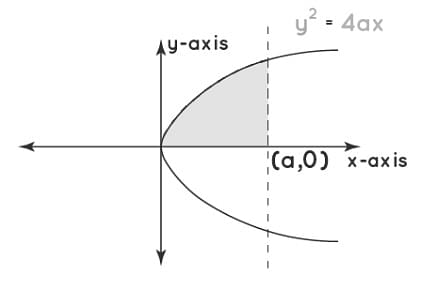
Area of a Parabola
The equation of the curve is y = (4ax) and the limit is from O to a.
A = 2Oa4ax.dx
A = 4\(\sqrt a\) O\(\int\)a\(\sqrt x\).dx
A = 4\( \sqrt a\) [\( \)\(^2/_3\) . x\(^3/_2\)]aO
A = 4a ((\(^2/_3\) . a\(^3/_2\)) - 0)
A = 8a2/3
Hence, the area of the parabola is given by 8a2/3.
Also Read: Increasing and Decreasing Functions in Calculus
Area Between a Curve and a Line
[Click Here for Sample Questions]
The area between a curve and a line can be calculated by doing integration of the difference between the area of the curve and area under the line.

Area Between a Curve and a Line
Here, the equation of the curve is y1 = f(x) and y2 = g(x). The formula for the area is given by;
A = \(\int\limits_a^b\) [f(x) - g(x)].dx
Also Read: Differentiation and Integration Formula
- Area Between Two Curves
The area between two curves can be calculated by subtracting the area of the smaller curve from the whole area under the curve.
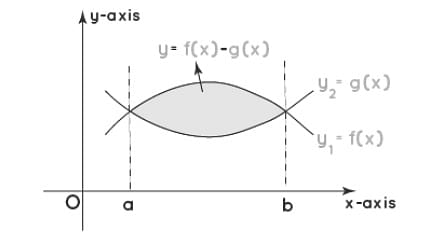
Area Between Two Curves
The equations of the curve are y1 = f(x) and y2 = g(x) and the area between the two curves is given by;
A = \(\int\limits_a^b\) [f(x) - g(x)].dx
Things to Remember
- Area under the curve is the total area enclosed by a curve line and an axis.
- The area under the curve is mainly calculated by the antiderivative method or integration method.
- To calculate the area under the curve by integration method, the equation of the curve, the axis enclosing the curve and the lower and upper limits are required.
- The area under the curve can also be calculated by dividing the curve into many smaller rectangles and adding their areas.
Also Read:
Sample Questions
Ques. Calculate the area under the curve of a function f(x) = 7 - x2, the limit is given as x = -1 to 2. (3 marks)
Ans. Area (A) = \(\int\limits_1^2\)(7 - x2) dx
= (7x - \(\frac{1}{3}\)x3) I2-1
= [7.2 - \(\frac{1}{3}\)(8)] - [7(-1) - \(\frac{1}{3}\)(-1)]
= [(42 - 8)/3] - [(1 - 21)/3]
= (34 + 20) / 3
= 54/3
= 18 sq. units
Ques. Find the area under the curve, for the region bounded by the circle x2 + y2 = 16 in the first quadrant. (3 marks)
Ans. x2 + y2 = 16
y =\( \sqrt 4^2\) - x2
A = O \(\int^4\) y.dx
= O4 42 - x2.dx
= [x/2 \( \sqrt 4^2\)- x2 + 42/2 sin-1x/4]O4
= [((4/2) O + (16/2)sin-11) - O]
= (16/2)(\(\prod\)2)
= 4\(\prod\)
Ques. Find the area under the curve, for the region enclosed by the ellipse x2/36 + y2/25 = 1. (3 marks)
Ans. x2/36 + y2/25 = 1
y = 5/6 \( \sqrt 6^2\) - x2
A = 4 \( O\int\)6 y.dx
= 4 \(O\int\)6 \(^5/_6\) 62 - x2..dx + 62/2 sin -1 x/6]O6
= 20/6 [ x/2 . 62 - x2. + 62/2 sin -1 x/6]O6
= 20/6 [ (6/2 O) + 62/2 . sin -1 1) - O]
= 20/6 36/2 /2
= 30
Ques. Find the area of the region bounded above by y = x2 + 1, bounded below by y = x, and bounded on the sides by x = 0 and x = 1. (2 marks)
Ans. A = 01 [ (x2 + 1) - x ] dx
= \(O\int^1\) (x2 - x + 1) dx
= \(O\int^1\)x3/3 - x2/2 + x ]01
= 1/3 - 1/2 + 1
= 5/6
Ques. Find the area between the two curves y = x2 and y = 2x - x2. (5 marks)
Ans. x2 = 2x - x2
2x2 - 2x = 0
2x (x - 1) = 0
x = 0 or 1
Therefore, the point of intersection are (0,0) and (1,1)
A = \(O\int^1\) [ (2x - x2) - x2 ] dx
A = \(O\int^1\)(2x - 2x2) dx
A = 2 \(O\int^1\) (x - x2) dx
A = 2 [ x2/2 - x3/3 ]01
A = 2 [ ½ - \( ^1/_3\) ]
A = 1/3
Ques. Find the area bounded by the ellipse x2/a2 + y2/b2 = 1 and the ordinates x = 0 and x = ae, where, b2 = a2 (1 - e2) and e <1. (2 marks)
Ans. Area = 2 0ae ydx = 2 b/a \( \sqrt a\)e a2 - x2 .dx
A = 2b/a [ x/2 a2 - x2 + \( \sqrt a^2\)/2 sin-1 x/a ]0ae
A = 2b/2a [ae a2 - \(\sqrt a^2\)e2 + a2sin-1e]
A = ab [e\( \sqrt 1\) -e2 + sin-1e
Ques. Find the area of the region enclosed between the two circles: x2 + y2 = 4 and (x - 2)2 + y2 = 4. (5 marks)
Ans. Equations of the given circles are:
x2 + y2 = 4 ……….(1)
(x - 2)2 + y2 = 4 ………..(2)
Solving equations 1 and 2,
(x - 2)2 + y2 = x2 + y2
x2 - 4x + 4 + y2 = x2 + y2
x = 1 ; y = ±\(\sqrt 3\)
Thus, the point of intersection are (1, 3) and (1, -3)
Required area = 2 [ 01y dx + 12 y dx ]
= 2 [ 014 - (x - 2)2. dx + 12 4 - x2 . dx
= 2 [½ (x - 2)4 - (x-2)2 + ½ 4sin-1(x-2/2)]01 + 2 [½ x4-x2 + ½ 4sin-1x/2]21
= [ (x - 2)4 - (x-2)2 + 4sin-1(x-2/2) ]01 + [ x4 - x2 + 4sin-1x/2]12
= [ (-3 + 4sin-1 (-½)) - 4sin-1(-1) ] + [ 4sin-11 - 3 - 4sin-11/2 ]
= [ (-3 - 4 /6) + 4 /2 ] + [ 4 /2 - 3 - 4 /6 ]
= ( -3 - 2/3 + 2 ) + ( 2 - 3 - 2/3 )
= 8/3 - 23
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:







Comments