
Collegedunia Team Content Curator
Content Curator
When the ratio of the four constant terms or variable terms is said to be equal, then they are known to be in proportion. To compare the two ratios, the symbols '::' or '=' are used. The first and the second term of L.H.S and R.H.S respectively, are called extremes. And the second and first terms of L.H.S and R.H.S respectively, are known as mean terms. The products of mean terms are equal to the products of extremes.
Read Also: Class 6 Mathematics Chapter 1 knowing our numbers
| Table of Contents |
Key terms: Proportion formula, Extreme term, Inverse proportion, mean, Product, Fraction
What is Proportion?
[Click Here for Sample Questions]
A fraction, share, or portion measured in comparison to a whole is referred to as proportion. When two ratios are comparable and equivalent, they are said to be in proportion. Proportion can be termed as a mathematical comparative analysis among two numbers. As per proportion, if two pairs of numbers increase or decrease in the same ratio, the ratios are directly proportional to one another. It is a formula or statement that shows that two ratios or fractions are equivalent.
For example, a bus traveling at 25 km/hr is similar to a bus traveling 100 kilometers in 4 hours because 25 km/hr = 100 km/4hrs = 25 km/hr. In proportion, the sequence of terms is significant. For example, the numbers 4, 7, 30, and 72 are in proportion, whereas the numbers 4, 7, 72, and 30 are not.
Read Also: Class 6 Mathematics Chapter 2 Whole Numbers
Proportion Formula
[Click Here for Sample Questions]
A proportion formula is a mathematical expression that can be applied to obtain comparative values. We follow the concept of proportion to answer proportion problems.
For example, two ratios are a : b and c : d is said to be in proportion. The terms ‘a’ and ‘d’ are called ‘extreme terms’ or ‘extremes’ and the terms ‘b’ and ‘c’ are known as ‘mean terms’ or ‘means’. The ‘Proportion Formula’ is expressed as below:
a : b :: c : d ⇒ \(\frac{a}{b}\) = \(\frac{c}{d}\)
For example, there is the same number of kids in two rooms and the number of girls and boys is equal. If the first ratio of girls to boys is 2:3 and the second is 1:2, the proportion is 2 : 4 :: 1 : 2 or 2/4 = 1/2. Also, the extremes terms are 2 and 2, while the mean terms are 4 and 1.
Types of Proportion
[Click Here for Sample Questions]
The proportion can be categorized into different kinds depending on what type of similarity two or more quantities share. Proportions can be divided into two categories:
- Direct Proportion – The direct relationship between two quantities is described as Direct Proportion. To put it another way, if one value rises, the other rises as well, and vice versa. For example, increasing the speed of a motorbike causes it to travel a greater distance in a given length of time. The direct proportion is expressed as x ∝ y.
- Indirect/Inverse Proportion – The indirect relationship between two quantities is described as Indirect Proportion. In simple language, if one value rises, the other decreases, and vice versa. For Example, by increasing the speed of the motorbike, a fixed distance can be covered in less time. The indirect proportion is expressed as x ∝ 1/y.
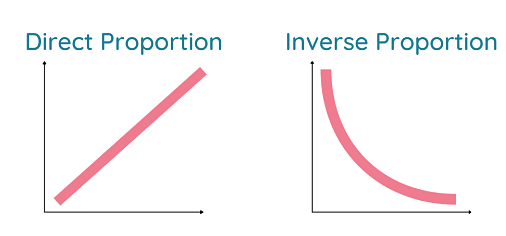
Types of Proportion
Read Also: Class 6 Mathematics Chapter 3 Playing with Numbers
Properties Of Proportion
[Click Here for Sample Questions]
A proportion, as we all know, is a mathematical term that indicates that two ratios are equal. In general, four numbers are proportional if the ratio of the first two terms is the same as the second and third. Following mentioned are the basic properties of proportion:
- The integers a, b, c, and d are in proportion if the ratio of the first two terms equals the ratio of the last two terms, like a : b :: c : d, which is written as ‘a is to b is as c is to d’. ‘Is as’ is represented by the symbol ‘::’.
- In a proportion, each value is known as its term, or it is proportionate.
- The first and last terms in a proportion are known as the ‘extremes’ or ‘extreme terms’, while the second and third terms are known as the ‘means’ or ‘mean terms’. For example, if four values a, b, c, and d are in proportion, then ‘a and d’ are ‘extremes’ and ‘b and c’ are known as ‘means’.
- The fourth proportionate term refers to the fourth term of a proportion.
- The product of the extreme terms equals the product of the mean terms for any proportion, which is, a : b :: c : d only if ad = bc.
- We can form three more proportions using the terms of a given proportion.
- If a : b = b : c, then a, b, and c are in continuous proportion, with b being the mean proportion amongst a and c and c being the third proportional to the first and second, that is, a and b.
Read Also: Maths formulas and solved examples
Things To Remember
- A fraction, share, or portion measured in comparison to a whole is referred to as proportion.
- When two ratios are comparable and equivalent, they are said to be in proportion.
- A proportion formula is a mathematical expression that can be applied to obtain comparative values. This is what we mean when we say two fractions are equivalent.
- If a : b & c : d is said to be in proportion then ‘a’ & ‘d’ are called ‘extreme terms’ or ‘extremes’ and the terms ‘b’ & ‘c’ are known as ‘mean terms’ or ‘means’.
- The direct relationship between two quantities is described as Direct Proportion. If one value rises, the other rises as well, and vice versa then expressed as x ∝ y.
- The indirect relationship between two quantities is described as Indirect Proportion. If one value rises, the other decreases, and vice versa then expressed as x ∝ 1/y.
Read Also: Class 6 Mathematics Chapter 4 Basic Geometrical Ideas
Sample Questions
Ques. Are 86, 91, 42, 8 in proportion? [1 Marks]
Ans. Extreme terms = 86 and 8
Mean terms = 91 and 42
Product of Extreme terms = 86 × 8 = 688
Product of Mean terms = 91 × 42 = 3822
Product of Extreme ≠ Product of Mean terms
Therefore, 86, 91, 42, 8 are not in proportion.
Ques. Find the missing number in the bracket in the following:- proportion: ( ) :4 : :8 :16 [1 Marks]
Ans. 8 : 16 = \(\frac{8}{16}\) = \(\frac{2 ×4}{4 ×4}\) = \(\frac{(2)}{4} \)
Therefore, the missing number in the bracket is 2.
Ques. Find the value of x in 3 : x :: 2 : 6 using the proportion formula. [2 Marks]
Ans. Proportion Formula = a : b :: c : d ⇒ \(\frac{a}{b} = \frac{c}{d}\)
Therefore, 3 : x :: 2 : 6 ⇒ \(\frac{3}{x} = \frac{2}{6}\)
⇒ \(\frac{3}{x} = \frac{2}{6}\)
x = 3 × \(\frac{6}{2}\)
x = \(\frac{18}{2}\)
x = 9
Ques. Are 6, 18, 54 in continued proportion? [2 Marks]
Therefore, 6, 18, 54 will be in continued proportion if 6, 18, 18, 54 are in proportion.
Product of Extreme terms = 6 × 54 =324
Product of Mean terms = 18 × 18 =324
Therefore, the Product of Extremes = Product of Means
Hence, 6, 18, 18, 54 are in proportion. Also, 6, 18, 54 are in Continuous Proportion.
Ques. What must be added in 6, 10, 14, 22 to be in proportion? [2 Marks]
Ans. Let the number to be added be x.
Now, 6 + x, 10 + x, 14 + x, 22 + x are meant to be in proportion.
⇒ Product of Extreme terms = Product of Mean terms
⇒ (6 + x) (22 + x) = (10 + x) (14 + x)
⇒ 132 + 6x + 22x + x2 = 140 + 10x + 14x + x2
⇒ 132 + 28x = 140 + 24x
⇒ 28x – 24x = 140 – 132
⇒ 4x = 8
⇒ x = \(\frac{8}{4}\)
⇒ x = 2
Ques. If 30 bananas are used to make 15 glasses of milkshake, then how many bananas do we need to make 100 glasses of milkshake? [2 Marks]
Ans. Let the number of bananas used to make 100 glasses of milkshake be x.
⇒\(\frac{x}{100} = \frac{30}{15}\)
⇒ Multiplying both sides by 100
⇒ x = \(\frac{30 ×100}{15}\)
⇒ x = \(\frac{3000}{15}\)
⇒ x = 200
Ques. Jessica runs 5 kilometers 40 minutes. At the same rate, how much she could run in 1 hour? [3 Marks]
Ans. Let the required distance be x.
Given that,
⇒ 5 kilometers in 40 minutes = x kilometers in 1 hour
⇒ 5 kilometers in 40 minutes = x kilometers in 60 minutes (1 hour = 60 minutes)
Therefore, the equation for a proportion will be,
⇒ \(\frac{5}{40} = \frac{x}{100}\)
⇒ x = \(\frac{(5 ×100)}{40} \)
⇒ x = \(\frac{500}{40}\)
⇒ x = 12.5
⇒ x = 12 kilometers and 500 meters
Hence, Jessica will be able to run 12 kilometers and 500 meters in 1 hour.
Ques. Are 6, 9, 2, 7 in proportion? [2 Marks]
Ans. Extreme terms = 6 and 7
Mean terms = 9 and 2
Product of Extreme terms = 6 × 7 = 42
Product of Mean terms = 9 × 2 = 18
Product of Extreme ≠ Product of Mean terms
Therefore, 6, 9, 2, 7 are not in proportion.
Ques. If 120 eggs are produced by 20 hens, then how many eggs will be produced by 50 hens? [2 Marks]
Ans. Let the number of eggs produced by 50 hens be x.
⇒ \(\frac{x}{50} = \frac{120}{20}\)
⇒ Multiplying both sides by 50
⇒ x = \(\frac{120 × 50}{20}\)
⇒ x = \(\frac{6000}{20}\)
⇒ x = 300
Therefore, 300 eggs will be produced by 50 hens.
Ques. Find the numbers whose sum is 140 and they are in the ratio of 2:5. [2 Marks]
Ans. Let the numbers be 2x and 5x. The sum of these two numbers given in the question is 140.
So, 2x + 5x = 140
7x = 140
x = 20
Therefore, the two numbers are
2x = 2 x 20 = 40
5x = 5 x 20 = 100
Ques. Check whether the following expressions are true or false. [2 Marks]
a) 14 : 16 = 24 : 58
b) 40 dogs : 200 dogs = 20 kg : 100 kg
Ans. a) 14 : 16 = 24 : 58
14 : 16 = \(\frac{14}{16}\) = \(\frac{7}{8}\) = 7 : 8
24 : 58 = \(\frac{24}{58}\) = \(\frac{12}{29}\) = 12 : 29
Therefore, they are unequal.
Hence, the given expression is false.
b) 40 dogs : 200 dogs = 20 kg : 100 kg
40 dogs : 200 dogs = 1 : 5
20 kg : 100 kg = 1 : 5
Therefore, they are equal.
Hence, the given expression is true.
Ques. The earnings of Shyam is 15000 rupees every month and Mohit is 250000 per year. If the monthly expenses of every person are around 8500 rupees. Find the ratio of the savings. [3 Marks]
Ans. Savings of Shyam per month = Rs (15000-8500) = Rs. 6500
Yearly income of Mohit = Rs. 250000
Hence, the monthly income of Mohit = Rs. 250000/12 = Rs. 20830 (approximately)
So, the savings of Mohit per month = Rs (20830 – 8500) = Rs. 12330
Therefore, the ratio of savings of Shyam and Mohit is Rs. 6500 : Rs. 12330 = 650 : 1233.
Ques. The length and breadth of a rectangular park are 80 meters and 20 meters. What is the ratio of the length and breadth of the park? [2 Marks]
Ans. Length of the rectangular park = 80 m
Breadth of the rectangular park = 20 m
Hence, the ratio of length to breadth = 80 : 20
⇒ 80 : 20 = 4 : 1.
Thus, the ratio of length and breadth of the rectangular park is 4 : 1.
Read Also:






Comments