
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Arithmetic Addition refers to the process of combining two or more integers in order to construct an addition table, and the plus sign (+) is the math symbol for an addition operation. The term ‘sum’ refers to the same addition operation, and the summation symbol (∑) can be used to represent a series of numbers for addition. The arithmetic operation of addition is used to calculate the total of two or more numbers.
The addition table aids with the addition of numbers by generating a pattern and arranging the numbers in rows and columns. The addition table allows us to rapidly get the sum of two integers without having to add them together. Addends are the numbers that are added to fill up the gaps in the addition chart. To fill a certain row of an addition table, we'll use the logic of adding numbers, keeping one addend constant while altering the other to fill in all the entries in that row, such as 1 + 1 = 2, 1 + 2 = 3, 1 + 3 = 4, and so on. The addition table, often known as the addition chart, is a tool used to help students learn how to add numbers.
| Table of Content |
Key Takeaways: Arithmetic Addition, summation symbol, addition operation, addition table, even number, ∑, +, integers, commutative, mathematical operation
Addition Tables
[Click Here for Sample Questions]
Below given is addition table for 1 to 10. The rows and columns of the table represent each number from 1 to 10.

Addition table
To understand the concept better, we are using the Addition Table given above. For instance, you wish to add the numbers 3 and 5 i.e., 5+3. Now to find the answer, you just need to walk down to the row with the number ‘5’ written on the table, and then along the column with the number ‘3’ to get your answer, which is ‘8’. Since Arithmetic Addition is a commutative mathematical operation, you may also travel along the row with the number ‘3’ written on it and then along the column with the number ‘5’ to reach your answer i.e., 8 (5+3 = 8).
Also read: Associative law
Explanation: Addition Table
[Click Here for Sample Questions]
We can write addition tables for each integer from 1 to 10. These can be written as:
| Addition Table of 1 |
| 1+1 = 2 |
| 2+1 = 3 |
| 3+1 = 4 |
| 4+1 = 5 |
| 5+1 = 6 |
| 6+1 = 7 |
| 7+1 = 8 |
| 8+1 = 9 |
| 9+1 = 10 |
| 10+1 = 11 |
| Addition Table of 2 |
| 1+2 = 3 |
| 2+2 = 4 |
| 3+2 = 5 |
| 4+2 = 6 |
| 5+2 = 7 |
| 6+2 = 8 |
| 7+2 = 9 |
| 8+2 = 10 |
| 9+2 = 11 |
| 10+2 = 12 |
| Addition Table of 3 |
| 1+3 = 4 |
| 2+3 = 5 |
| 3+3 = 6 |
| 4+3 = 7 |
| 5+3 = 8 |
| 6+3 = 9 |
| 7+3 = 10 |
| 8+3 = 11 |
| 9+3 = 12 |
| 10+3 = 13 |
| Addition Table of 4 |
| 1+4 = 5 |
| 2+4 = 6 |
| 3+4 = 7 |
| 4+4 = 8 |
| 5+4 = 9 |
| 6+4 = 10 |
| 7+4 = 11 |
| 8+4 = 12 |
| 9+4 = 13 |
| 10+4 = 14 |
| Addition Table of 5 |
| 1+5 = 6 |
| 2+5 = 7 |
| 3+5 = 8 |
| 4+5 = 9 |
| 5+5 = 10 |
| 6+5 = 11 |
| 7+5 = 12 |
| 8+5 = 13 |
| 9+5 = 14 |
| 10+5 = 15 |
Also read: Multiplication and division of integers
| Addition Table of 6 |
| 1+6 = 7 |
| 2+6 = 8 |
| 3+6 = 9 |
| 4+6 = 10 |
| 5+6 = 11 |
| 6+6 = 12 |
| 7+6 = 13 |
| 8+6 = 14 |
| 9+6 = 15 |
| 10+6 = 16 |
| Addition Table of 7 |
| 1+7 = 8 |
| 2+7 = 9 |
| 3+7 = 10 |
| 4+7 = 11 |
| 5+7 = 12 |
| 6+7 = 13 |
| 7+7 = 14 |
| 8+7 = 15 |
| 9+7 = 16 |
| 10+7 = 17 |
| Addition Table of 8 |
| 1+8 = 9 |
| 2+8 = 10 |
| 3+8 = 11 |
| 4+8 = 12 |
| 5+8 = 13 |
| 6+8 = 14 |
| 7+8 = 15 |
| 8+8 = 16 |
| 9+8 = 17 |
| 10+8 = 18 |
| Addition Table of 9 |
| 1+9 = 10 |
| 2+9 = 11 |
| 3+9 = 12 |
| 4+9 = 13 |
| 5+9 = 14 |
| 6+9 = 15 |
| 7+9 = 16 |
| 8+9 = 17 |
| 9+9 = 18 |
| 10+9 = 19 |
| Addition Table of 10 |
| 1+10 = 11 |
| 2+10 = 12 |
| 3+10 = 13 |
| 4+10 = 14 |
| 5+10 = 15 |
| 6+10 = 16 |
| 7+10 = 17 |
| 8+10 = 18 |
| 9+10 = 19 |
| 10+10 = 20 |
Tips for addition table
[Click Here for Sample Questions]
- When we add 0 to a number, it has no effect; for example, 7 + 0 Equals 7, 6 + 0 = 6, 89 + 0 = 0.
- When we add a set of numbers, the result is the same regardless of their order or sequence, for example, 8 + 7 + 3 + 2 = 20 and 7 + 2 + 3 + 8 = 20.
- We arrange the numbers in a column to execute the mathematical operation of addition on a large list of numbers and then quickly receive the result.
- When we add 1 to an even number, we get a new number, for example, 4 + 1 = 5, 8 + 1 = 9.
- If we add two even numbers, the outcome is also an even number, as in 8 + 2 = 10, 6 + 4 = 10.
- If we add 1 to a number, the outcome is the number immediately after the number in the question, for example, 7 + 1 = 8, 5 + 1 = 6.
Also read: Greatest integer function
Example: Find all of the row 5 elements in the addition table 1-10.
Solution: We’ll keep the number 5 as a constant addend and alter the second addend from 1-10 to discover the items of row 5 in the addition table 1-10. 5 + 1 Equals 6, 5 + 2 = 7, 5 + 3 = 8. 5 + 3 = 8, 5 + 4 = 9, 5 + 5 = 10, 5 + 6 = 11, 5 + 7 = 12, 5 + 8 = 13, 5 + 9 = 14, 5 + 10 = 15. 5 + 3 = 8, 5 + 4 = 9, 5 + 5 = 10, 5 + 6 = 11, 5 + 7 = 12, 5 + 8 = 13, 5 + 9 = 14, 5 + 10 = 15.
As a result, row 5's values are 6, 7, 8, 9, 10, 11, 12, 13, 14, and 15.
Things To Remember
- Arithmetic Addition refers to the process of combining two or more integers in order to construct an addition table, and the plus sign (+) is the math symbol for an addition operation.
- The addition table aids with the addition of numbers by generating a pattern and arranging the numbers in rows and columns.
- The addition table allows us to rapidly get the sum of two integers without having to add them together.
- Addends are the numbers that are added to fill up the gaps in the addition chart.
- The addition table, often known as the addition chart, is a tool used to help students learn how to add numbers.
Sample Questions
Ques. Add the numbers 4 and 4, using the given Addition Table. [5 marks]
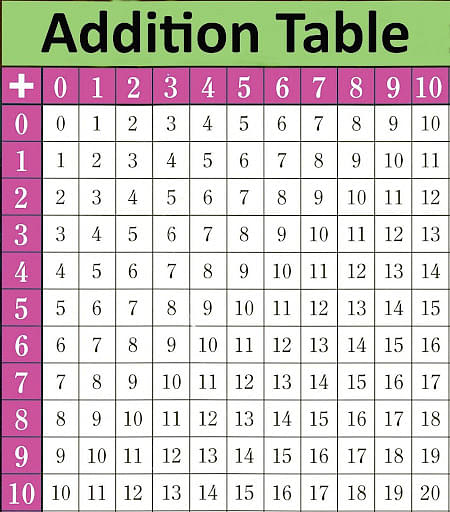
Ans. The addition table allows us to rapidly get the sum of two integers without having to add them together. Addends are the numbers that are added to fill up the gaps in the addition chart. To fill a certain row of an addition table, we'll use the logic of adding numbers, keeping one addend constant while altering the other to fill in all the entries in that row.
When we walk down the row with the number 4 and across the column with the number 4, the equivalent item in the addition table at the junction point is 8.
We can also move down the fourth row and across the fourth column to find the number 4. The matching value, which is 8, will also get the same outcome, that is 8.
Ques. Explain the Addition Table for 7. [3 marks]
Ans. The addition table for the number 7 has been explained in the table given below:
| Addition Table of 7 |
| 1+7 = 8 |
| 2+7 = 9 |
| 3+7 = 10 |
| 4+7 = 11 |
| 5+7 = 12 |
| 6+7 = 13 |
| 7+7 = 14 |
| 8+7 = 15 |
| 9+7 = 16 |
| 10+7 = 17 |
Ques. What is Arithmetic Addition in Mathematics? [2 marks]
Ans. The addition table aids with the addition of numbers by generating a pattern and arranging the numbers in rows and columns. The addition table allows us to rapidly get the sum of two integers without having to add them together. Addends are the numbers that are added to fill up the gaps in the addition chart.
Ques. Add the numbers 8 and 1 by using the Addition Table. [3 marks]
Ans. To read the addition table, we must look at the addends provided and observe them down the row and across the column to determine where they meet in the table. The solution is '9' (8+1 = 9) by walking down the row with the number '8' written on the table and then along the column with the number '1'. When 1 is added to any even number, the new number formed is an added number.
Ques. Explain the Addition Table for 12. [3 marks]
Ans. The addition table for the number 12 has been explained in the table given below:
| Addition Table of 12 |
| 1+12 = 13 |
| 2+12 = 14 |
| 3+12 = 15 |
| 4+12 = 16 |
| 5+12 = 17 |
| 6+12 = 18 |
| 7+12 = 19 |
| 8+12 = 20 |
| 9+12 = 21 |
| 10+12 = 22 |
Ques. Explain the the addition table for 20 [3 marks]
Ans. The addition table for the number 20 has been explained in the table given below:
| Addition Table of 20 |
| 1+20 = 21 |
| 2+20 = 22 |
| 3+20 = 23 |
| 4+20 = 24 |
| 5+20 = 25 |
| 6+20 = 26 |
| 7+20 = 27 |
| 8+20 = 28 |
| 9+20 = 29 |
| 10+20 = 30 |
Ques. Explain the addition table for 32. [3 marks]
Ans. The addition table for the number 32 has been explained in the table given below:
| Addition Table of 32 |
| 1+32 = 33 |
| 2+32 = 34 |
| 3+32 = 35 |
| 4+32 = 36 |
| 5+32 = 37 |
| 6+32 = 38 |
| 7+32 = 39 |
| 8+32 = 40 |
| 9+32 = 41 |
| 10+32 = 42 |
Ques. Explain the addition table for 16. [3 marks]
Ans. The addition table for the number 16 has been explained in the table given below:
| Addition Table of 16 |
| 1+16 = 17 |
| 2+16 = 18 |
| 3+16 = 19 |
| 4+16 = 20 |
| 5+16 = 21 |
| 6+16 = 22 |
| 7+16 = 23 |
| 8+16 = 24 |
| 9+16 = 25 |
| 10+16 = 26 |
Ques. Using the addition table, how will you find the value of 9+8? Briefly describe the situation. [4 marks]
Ans. In order to find the value of 9+8, we can use two different ways to read the addition table given below. This is because addition usually follows Commutative Property which means 9+8 = 8+9.
When we walk down the row with the number 9 and across the column with the number 8, the corresponding item in the addition table at the junction point is 17. We can also go down the row with the number 8 and across the column with the number 9 to find the answer. The comparable value, 17, will also get the same outcome.
Ques. How to read an Addition Table? [5 marks]
Ans. Certain tips for easy reading of the Addition Table have been listed below for your reference:
- Adding 0 to an integer has no impact; for example, 7 + 0 equals 7, 6 + 0 equals 6, and 89 + 0 equals 0.
- When we add a group of integers, regardless of their order or sequence, the outcome is the same, for example, 8 + 7 + 3 + 2 = 20 and 7 + 2 + 3 + 8 = 20.
- We arrange the numbers in a column to perform the addition mathematical operation on a huge list of numbers and retrieve the result quickly.
- We receive a new number when we add 1 to an even number, for example, 4 + 1 = 5, 8 + 1 = 9.
- When two even numbers are added together, the result is also an even number, as in 8 + 2 = 10, 6 + 4 = 10.
Related links:







Comments