Even and Odd Numbers: Definition, Difference, Properties & Solved Examples

Even and odd numbers are further classifications of whole numbers in Mathematics. Both the odd and even numbers are unique, that is, there is no existing number that is both even and odd. A number is either even or odd. To put the definition of even and odd numbers in simple terms, we can say that even numbers are those numbers that are completely divisible by the number 2 and odd numbers are those numbers that are not completely divisible by two. Also, Zero is considered to be an even number because it is an integer multiple of 2, that is, 0 x 2 = 0.

Key Terms: Even Numbers, Odd Numbers, Whole Numbers, Integers, Equal Groups, Divisibility by 2, Natural Numbers, Real Numbers, Remainder

---

What are Even and Odd Numbers?

[Click Here for Sample Questions]

Even numbers are those numbers that can be divided into two equal groups. Similarly, odd numbers are those numbers that cannot be divided into two equal groups. More clearly, they can be defined as follows:

• An even number is a number which is divisible by 2, with 0 as the remainder, that is, completely divisible by 2.
• An odd number is a number that is not divisible by 2, leaving 1 as the remainder, that is, not completely divisible by 2.

Even Numbers & Odd Numbers

Read More: Number System

---

Set Representation of Even and Odd Numbers

[Click Here for Sample Questions]

The sets of even numbers and odd numbers can be represented in the following ways:

• The set of even numbers is written as {x : x = 2k, where k ∈ W}, where k is any integer and W is the set of whole numbers. 
• The set of odd numbers is written as {x : x = 2k + 1, where k ∈ W}, where k is any integer and W is the set of whole numbers. 
• A proper definition of an even number is of the form n = 2k, where n and k are any integers, and a proper definition of an odd number is of the form n = 2k + 1, where n and k are any integers.

---

Difference Between Even and Odd Numbers

[Click Here for Sample Questions]

The following are the most important differences between even numbers and odd numbers:

• All even numbers are completely divisible by 2 whereas no odd number is completely divisible by 2.
• If the digit in the ones place of any given number is even, then that number is considered to be an even number. Likewise, if the digit in the ones place of any given number is odd, then that number is considered to be an odd number.
• While even numbers can be separated into pairs, odd numbers cannot be separated into pairs.

Read More: Addition and Subtraction of Integers

---

Properties of Even and Odd Numbers

[Click Here for Sample Questions]

There are several properties of even and odd numbers that make them highly useful in solving problems. They are

• A sum of two even numbers is an even number only, for example, 2 + 4 = 6, an even number.
• A sum of an even number and an odd number is an odd number. For example, 1 + 8 = 9, an odd number.
• A sum of two odd numbers is an even number, for example, 3 + 5 = 8, an even number.
• A difference between two even numbers is an even number. For example, 14 – 10 = 4, an even number.
• A difference between an even number and an odd number is an odd number. For example, 12 – 7 = 5, an odd number; or for example, 19 – 16 = 3, an odd number.
• A difference of two odd numbers is an even number. For example, 13 – 9 = 4, an even number.
• A product of two even numbers is an even number. For example, 18 x 20 = 360, an even number. 
• A product of an even number and an odd number is an even number. For example, 11 x 22 = 242, an even number. 

Also Read: Real Numbers

Even and Odd Numbers Chart 

The following is a chart of all even and odd numbers till 100. The numbers in yellow colour are all odd numbers whereas the numbers in blue are all even numbers. With this chart, it is easy to see that all even numbers end in 0, 2, 4, 6 or 8 and all odd numbers end in 1, 3, 5, 7 or 9. 

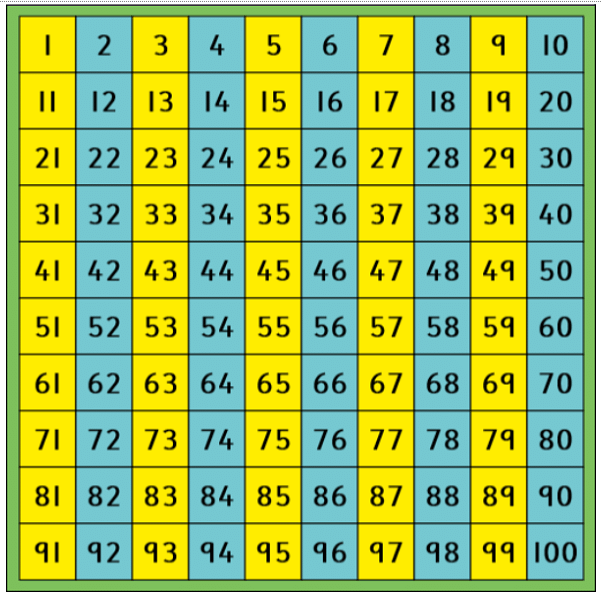
Even and Odd Numbers Chart

---

How to Find Even and Odd Numbers?

[Click Here for Sample Questions]

There are a number of easy methods to identify if a given number is an even number or an odd number.

• All even numbers end in 0, 2, 4, 6 or 8 and all odd numbers end in 1, 3, 5, 7 or 9. Therefore, by looking at the digit in the ones place of any given number, we can identify whether it is an even number or an odd number. 
• In the set of all counting numbers, each alternate number beginning from 1 is an odd number and each alternate number beginning from 2 is an even number. 
• We can also find out if a given number is an even number or an odd number by checking its divisibility by 2. If it is completely divisible by 2, it is an even number and if it is not completely divisible by 2, it is an odd number. 
• All non-integers cannot be classified into either the set of even numbers or the set of odd numbers.

Odd and Even Numbers

Read More: Multiplication and Division of Integers

---

What are Even and Odd Decimals?

[Click Here for Sample Questions]

Decimal numbers are neither even numbers nor odd numbers because they are not whole numbers or integers. Only integers or whole numbers can be either even numbers or odd numbers. Zero is an integer that is divisible by 2, which is why 0 is considered to be an even number. 

Read More: Decimal Expansion of Rational Numbers

---

Why is Zero an Even Number?

[Click Here for Sample Questions]

Zero is considered to be an even number because it is an integer multiple of 2, that is, 0 x 2 = 0.

---

Things to Remember

[Click Here for Sample Questions]

• Even numbers and odd numbers are exclusive sets, that is, a given number cannot be both even and odd. 
• An even number can be defined as a number that is exactly divisible by 2.
• An odd number can be defined as a number that is not exactly divisible by 2.
• Zero is an even number because it is an integer multiple of 2, that is, 0 x 2 = 0.
• A decimal or a fraction cannot be either even or odd.

---