
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Estimation is the method of rounding off the digits of a number so as to make the calculations easy and quicker. It does not give the exact value, but instead, an approximate value is the result of the calculation, which is almost close to the exact value of the calculation. If a person calculating a value is not looking to find the exact value of any calculation but instead is looking to find the approximate value of the calculations, then one can use the method of estimation by the method of rounding off. In simpler terms, Estimation of a number refers to a reasonable guess of the actual value to make calculations easier and more realistic.
| Table of Contents |
Key Terms: Estimation, Rounding Off, Approximate Values, Place Value, Complex Calculations, Whole Number, Round Up, Round Down
Estimation of Numbers (Rounding Off Method)
[Click Here for Sample Questions]
Estimation refers to the process of approximating a quantity to the required accuracy. It involves rounding off the numbers that are involved in the calculation to get a quick and rough answer. In the field of Mathematics, estimating values of even the lengthiest of calculations is something that every individual practice in day to day life.
All of our day-to-day activities involve estimation subconsciously. In estimation, numbers are rounded to a specific place value in order to make them the closest to a whole number.
General Rules of Estimation
[Click Here for Sample Questions]
There are some rules that are followed while rounding off the numbers or finding the estimated number.
- If the number is equal to or more than 5, then the number is rounded off the digit to the next whole number and we increase the digit by 1. E.g. 5.6 and 6.5 would be rounded off to 6 and 7 respectively.
- If the number is less than 5, i.e., 0, 1, 2, 3, 4, we leave the digit alone (round down). E.g. 41.1 would be rounded off to 41.
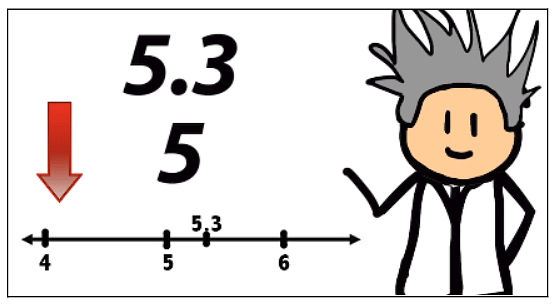
Estimation of Numbers
Read More: Difference Between Fraction and Rational Numbers
Estimating to Different Place Values
[Click Here for Sample Questions]
There is a requirement to round off different numbers to different place values according to the requirement of the calculations. Following are the examples of rounding off to different place values for 12,123.65
- To The Nearest Whole Number
For rounding off to the nearest whole number, only the decimal digits need to be removed. So, by rounding off 12,123.65 to the nearest whole number we get 12,124.
- To The Nearest Tenth
For rounding off to the nearest tenth, the number needs to be rounded off till the ones place. So, by rounding off 12,123.45 to the nearest tenth we get 12,120.
- To The Nearest Hundredth
For rounding off to the nearest hundredth, the number needs to be rounded off to the tens place. So, by rounding off 12,123.45 to the nearest hundredth we get 12,100.
- To The Nearest Thousand
For rounding off to the nearest thousand, the number needs to be rounded off to the hundredth place.
2 is in the thousands place. The digit to its right is 1
So, we round down 2 i.e., we leave the digit alone
So, by rounding off 12,123.45 to the nearest thousand we get 12,000.

Estimation of A Sum of Numbers
Read More: Decimal Expansion of Rational Numbers
Application of Estimation of Numbers
[Click Here for Sample Questions]
The method of Estimation is used to make an approximate judgment about the worth of anything, be it amount, be it weight, be it size, or be it any other thing that can be approximated. This is usually done in order to avoid any complexities that might be faced during the calculation of numbers. Estimation is also well known because it saves a lot of time for the person who is doing any complex calculation.
Estimation is rounding off the numbers to their nearest convenient values so as to make the approximation. The exact solution may have a different value but has it very close to the one which is estimated.
Things to Remember
- Estimation of a number is a process of making a reasonable guess of the actual value to make calculations easier and more realistic.
- If the digit to the right of the given number is between 0 to 4 i.e., 0, 1, 2, 3, 4, then we leave the digit alone (round down).
- If the digit to the right of the given number is between 5 to 9 i.e., 5, 6, 7, 8, 9, then we increase the digit by 1 (round up).
- Lastly, any extra digits that have not been rounded off are removed.
- Estimation is quite useful to avoid any complexities that might be faced during the calculation of large numbers.
Sample Questions
Ques. Calculate the approximate value of 86.12. (3 Marks)
Ans. The digit next to 1 is 2. The number 2 is less than 5, so, we will retain the same number. Now, the number next to 6 is 1. Since the number 1 is less than 5, so, we will retain the same number. Thus, we will be rounding and estimating by rounding off the 86 to the same whole number that is 86. Thus, the approximate value of 86.12 is 86.
Ques. What is the difference between an exact value and an approximate value? (3 Marks)
Ans. The exact value can be calculated only by doing the perfect calculations without altering any value of the digits of the initial numbers, whereas Approximate values are the values calculated after rounding off the initial digits of the given numbers to make the calculations easy.
Ques. Ritu and John have collected 335 and 442 marbles respectively. What will be a better estimate to find the number of marbles they own together? (3 Marks)
Ans. We can find a better estimate by rounding off the digits to the nearest tens.
To get an estimate of the sum, we will first-round off all the numbers to the same place value, then add them.
Number of marbles Tia collected = 335 rounded off to 340
Number of marbles John collected = 442 rounded off to 440
Thus, the total number of marbles is 340 + 440 = 780
Ques. Can approximate values be converted into exact values after calculations are done? (3 Marks)
Ans. No, an approximate value cannot be converted into an exact value after the calculations are done, that’s why when an exact value is required, we cannot use the method of estimation by rounding off, as it does not have the exact value.
Ques. Calculate the estimated value of 8.6. Explain your answer. (3 Marks)
Ans. 6 is greater than 5, therefore it will be rounded off to the next whole number, making the number preceding one more than its previous value. Hence, the number becomes 9.0 or 9. Hence the estimated number of 8.6 is 9.
Ques. How useful are the estimated values in real life? (2 Marks)
Ans. In real life, usually, the approximate values are required and the approximated or estimated value that is obtained after rounding off is pretty close to the exact values of these calculations. Hence, estimation is very useful in daily life.
Ques. Calculate the approximate value of 86.23 to the nearest tenth. (3 Marks)
Ans. 3 is less than 5, therefore it will be rounded off to the previous digit, making the number 86.20. Then, 2 is also less than 5, so we will retain the number. Also, 6 is greater than 5, so we will round up 86 and add one to the previous Digit. Hence the estimated number to the nearest tenth of 86.23 is 90.
Ques. Calculate the estimated value of 55.12. Explain your answer. (3 Marks)
Ans. 2 is less than 5, therefore it will be rounded off to the previous digit, making the number 55.10. Then, 1 is also less than 5 hence we will retain the same number. Thus, we will be rounding and estimating by rounding off 55 to the same whole number that is 55. Hence the estimated number of 55.12 is 55.
Read Also:







Comments