
Collegedunia Team Content Curator
Content Curator
Class 11 Maths NCERT Solutions Chapter 1 are provided in the article below. In mathematics, a set refers to a collection of fixed objects like geometrical shapes, points in space, alphabetical letters, numbers, symbols, etc.
Class 11 Mathematics Chapter covers important concepts including Set Operations, Union of Sets, Venn Diagrams, and Properties of Sets.
Download: NCERT Solutions for Class 11 Mathematics Chapter 1 Sets pdf
Class 11 Maths NCERT Solutions Chapter 1 Sets
Class 11 Maths NCERT Solutions Chapter 1 Sets are as provided below:











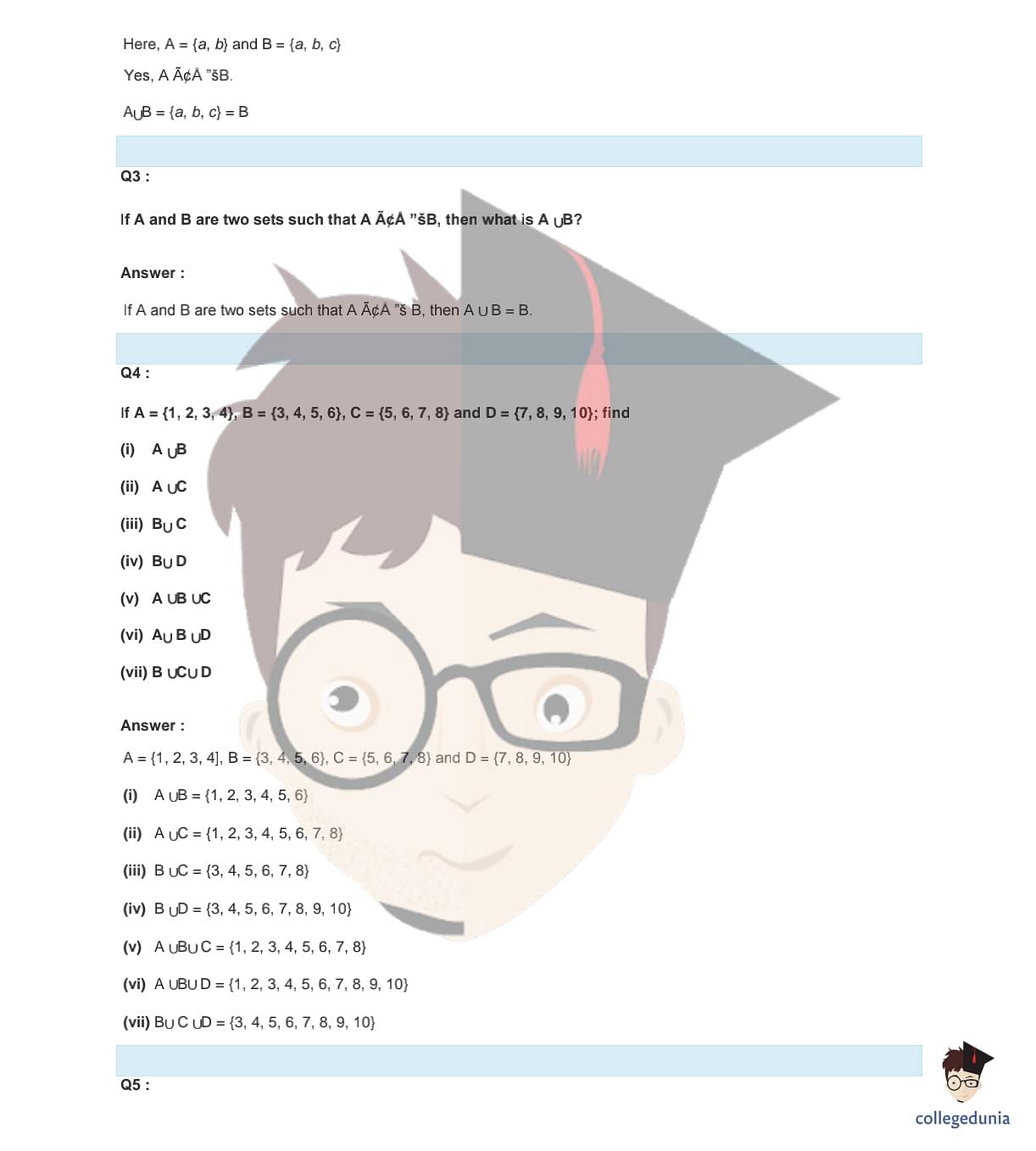




























Also check: Sets
Important Topics for Class 11 Maths NCERT Solutions Chapter 1 Sets
Important Topics for Class 11 Maths NCERT Solutions Chapter 1 Sets are as follows:
- Sets and their Representations
Sets are represented as a collection of well-defined objects/elements. A set is represented by a capital letter. The number of elements in the finite set is known as the cardinal number of a set.
| Representation of Sets and its elements is done as follows:
|
- The Empty Set
The empty set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero.
| Example: Determine if the given set is an empty set. P = {set of prime numbers divisible by 6}. Solution: Given: P = {set of prime numbers divisible by 6} As per the definition of prime numbers, prime numbers are the numbers that have only two factors, that are, 1 and the number itself. Therefore, no prime numbers are divisible by 6. This implies that the given set is an empty set. |
- Finite and Infinite Sets
Finite sets are countable and contain a finite number of elements. The set which is not finite is known as the infinite set.
| Example 3: Given, Set T = {….., -2, -1, 0}. Find out whether the given set is a finite or infinite set. Solution: Set T = {….., -2, -1, 0} is an infinite set because the elements of the set T start from negative of infinity and hence, cannot be finite. |
- Equal Sets
Equal sets are sets in which the number of elements is the same and all elements are equal.
| Example: Check if the sets A = {a, e, i, o, u} and B = {e, i, a, o, u} are equal sets or unequal sets. Solution: The order of the elements does not impact the equality of the two sets. Thus, set B can be written as B = {a, e, i, o, u} after rearranging the elements of B. Hence, A = {a, e, i, o, u} = B Thus, Sets A and B are equal sets. |
- Subsets
A subset is a part of given set. The set notation to represent a set A as a subset of set B is written as:
| A ⊆ B |
- Venn Diagrams
A Venn diagram visually represents the differences and similarities between two concepts. Venn diagrams are also called logic or set diagrams and are widely used in set theory, logic, mathematics, computer science, and statistics.
NCERT Solutions For Class 11 Maths Chapter 1 Exercises:
The detailed solutions for all the NCERT Solutions for Chapter 1 Sets under different exercises are as follows:
- NCERT Solutions for Chapter 1 Exercise 1.1 Solutions
- NCERT Solutions for Chapter 1 Exercise 1.2 Solutions
- NCERT Solutions for Chapter 1 Exercise 1.3 Solutions
- NCERT Solutions for Chapter 1 Exercise 1.4 Solutions
- NCERT Solutions for Chapter 1 Exercise 1.5 Solutions
- NCERT Solutions for Chapter 1 Exercise 1.6 Solutions
- Miscellaneous Exercise On Chapter 1 Solutions
Also check:
| Chapter Related Topics | ||
|---|---|---|
| Types of Sets | De Morgan’s Laws | Set Theory Symbols |
| Set Formulas | Number Theory | Group Theory |
| Universal Set | What is disjoint set | Equal equivalent sets |
Also check:





Comments