
Arpita Srivastava Content Writer
Content Writer
Continuity and Differentiability is an important unit in class 12 mathematics from the perspective of both boards and other competitive exams. It provides in-depth knowledge about the basics of continuity, differentiability, and the relation between them.
- Continuity and Differentiability will determine the value of derivatives of various quantities.
- It solves mathematic concepts such as logarithmic functions, exponential functions.
- The function solves continuity at a point, continuity on an interval and derivative of a function.
- The results are complementary to a function.
- Continuity function gives a graphical representation of a function in the form of a continuous wave.
- Differentiability function derives value for each domain.
- It is defined for closed interval [a, b].
- Continuous at the point x = a, if Limx→af(x)=f(a).
- It is differntiable at the same point x = a, if Limx→af′(a)=(f(a+h)−f(a))/h
Read More: Application of Derivatives
Key Terms: Continuity and Differentiability, Fundamental Rules, Logarithmic Functions, Exponential Functions, Continuity, Differentiability, Real Number, Domain, Chain Rule
What is Continuity and Differentiability?
[Click Here for Sample Questions]
Continuity and Differentiability are complementary functions. The concepts can solve both geometrical and algebraic functions. First, a function needs to be proved continuous for a point x=a.
- To determine the differential value, imagine that a function has a continuous domain value.
- The graph of the function does not have an intermediate value.
- It does not break in between the values of a function.
- Launching a rocket is a real-life example of continuity and differentiability.
- Suppose you want to use digital video recording equipment to record your playing video.
- The video comes out as a continuous function.
Solved Example of Continuity and Differentiability
 |
Read More:
| Chapter Related Concepts | ||
|---|---|---|
| Value of e | Quotient | Exponential growth formula |
| Approximation | Derivative of Inverse Trigonometric Functions | Infinity |
Definition of Continuity
[Click Here for Sample Questions]
The term 'continuity' is derived from the word continuous, which means an endless or unbroken path. Continuity of a function can be better understood if defined in terms of limits.
- A real function f(x) can be considered as continuous at a point say, x = a, if the function f(x) is approaching to a is f(a).
limx -> a f(x) = f(a)
- The function must be continuous throughout its path at every point in its domain.

Continuity Defination
Conditions for continuity of a function
For any function to be continuous, it must meet the following conditions:
- The function f(x) specified at x = a, is continuous only if f(a) belongs to real number.
- The limit of the function as x approaches a, exists.
- It must be equal to the function value at x = a.
Solved Example of ContinuityExample: Show that f(x) is continuous at x = 4 for the function f(x) = (x2 – 2x)/ (x – 3) Solution: Given function f(x) = (x2 – 2x)/ (x – 3) Substituting f(x) at x = 4, i.e., f(4) = (42 – 2(4))/ (4 – 3) We get the answer as 8. Since, we get the result as 8 for x = 4, i.e., f(4) = f(x) Therefore, as the answer for both f(4) and f(x), appears to be the same, the function is considered as continuous. |
Read More: Differentiation Rules

Defination and Conditions of Continuity
Discover about the Chapter video:
Continuity and Differentiability Detailed Video Explanation:
Read More:
Geometrical Representation of Continuity
[Click Here for Previous Years Questions]
A function f shall be continuous at x = a, only if there is no break in the graph of the function at the point (a, f(a)). In the case of an interval, a function is said to be continuous if there are zero intervals in the graph of the given function throughout the interval.

Geometrical Representation of Continuity
Definition of Differentiability
[Click Here for Sample Questions]
A function f(x) is differentiable at a point x = a, if f ' (a), i.e., the derivative of the function exists at each point of its domain.
- The differentiability of a function is represented as:
f ' (x) = f (x + h) – f(x) / h
- If a function f is continuous at any point, the same function is also differentiable at any point x = c in its domain.


Read More: Non-Parametric Test
Important Differentiability Formula
[Click Here for Previous Years Questions]
Some of the important differentiability formula are as follows:
Algebric Functions
Some important algebric functions are as follows:
- d(u+v) / dx = du/dx + dv/dx
- d/dx(uv) = udv/dx + vdu/dx
- d/dx(u/v) = vdu/dx - udv/dx / v2
Trigonometric Functions
Some important trigonometric functions used in continuity and differentiability are as follows:
| Sl. No | Functions |
|---|---|
| 1. | d/dx(sin x) = cos x |
| 2. | d/dx(cos x) = -sin x |
| 3. | d/dx(tan x) = sec2 x |
| 4. | d/dx(cot x) = cosec2 x |
| 5. | d/dx(sec x) = sec x tan x |
| 6. | d/dx(cosec x) = -cosec x cot x |
| 7. | d\dx(sin-1 x) = 1 / √1 – x2 |
| 8. | d\dx(cos-1 x) = -1 / √1 – x2 |
| 9. | d\dx(tan-1 x) = 1 / 1 + x2 |
| 10. | d\dx(cot-1 x) = -1 / 1 + x2 |
| 11. | d\dx(sec-1 x) = 1 / |x| √x2 – 1 |
| 12. | d\dx(cosec-1 x) = -1 / |x| √x2 – 1 |
Read More:
Theorem on Continuity and Differentiability
[Click Here for Sample Questions]
The important theorems on continuity and differentiability are as follows:
Theorem 1
Two function f(x) and g(x) are said to be continuous in real-value at point x =d, then we have
- f(x) + g(x) is continuous at the point x = d
- f(x) - g(x) is continuous at a point x = d
- g(x).g(x) is continuous at point x = d
- f(x)/g(x) is continuous at a point x = d, provided g(d) ≠ 0
Theorem 2
For functions f(x) and g(x) such that the composite function fog(x) will be defined at point x = d. If g(x) is continuous at point x = d and the function f(x) is continuous at function g(d), then function fog(x) is continuous at x = d.
Theorem 3
For a given function f(x) which is differentiable at point d then function is continuous at point d. This proves that differential function is continuous.
Theorem 4
Let f : [a,b], -> R be continuous on [a,b] and differentiable on (a, b), such that f(a) = f(b), where a & b are some real numbers. Then at least one point 'c' must exist in (a, b), such that f ' (c) = 0. It is also known as Rolle’s Theorem.
Theorem 5
The theorem is based on Mean Value / Lagrange Theorem. Let f : [a,b] -> R be a continuous function on [a,b] and differentiable on (a,b). Then there exists at least one point 'c' in (a,b) such that
f ' (c) = \(\frac{f (b) - f (a)}{b-a}\)

Theorem 6
This theorem is based on Chain rule. Chain rule is basically used to differentiate the composite of functions. Let us suppose a function f= vou, if t=u(x), and both dt/dx and dv/dt exists, then
df/dx = dv/dt. dt/dx
Read More: Logarithm Formula
Things to Remember
- Continuity and Differentiability function y = f(x) is defined over a closed interval [a, b].
- To determine whether a function is continuous, draw a graph without lifting a pen.
- It is used to determine the profit and loss value in a marketplace.
- The function works on determining the root of a function.
- The graph drawn for continuity and differentiability function is not sharp at the edges.
Read More: Methods of Integration
Previous Years Questions
- Define f(x)f(x) as the product of two real functions f1(x)=x,x∈f1(x)=x,x∈ R, and f2(x)
- d2xdy2 equals :
- ddx{cosec−1(1+x22x)} is equal to
- ddx(tan−1(√x−√a1+√xa)), x, a>0, is
- Derivative of the function f(x)=log5(log7x), x>7 is
- Differential coefficient of √sec√xsecx is
- Differential coefficient of tan−12x1−x2 with respect to sin−12x1+x2 will be
- For a>0,t∈(0,π2), let x=√asin−1t and y=√acos−1t, Then 1+(dydx)2 equals :
- If $f(x) = cosx \cdot cos \,2x \cdot cos \,4x \cdot cos \,8x \cdot cos \,16x$, then the value of $f '\left(\frac{\pi}{4}\right)$ is
- If g is the inverse function of f and f′(x)=sinx, then g′(x) is
- If sec(x2−2xx2+1)=y, then dydx is equal to
- If x=acosθ,y=bsinθ, then d3ydx3 is equal to
- If x=exp{tan−1(y−x2x2)}, then dydx equals
- If x=sintcos2t and y=costsin2t, then at t=π4, the value of dydx is equal to :
- If y=√(1+cos2θ1−cos2θ) , then dydθ at θ=3π4 is:
- If y=2x⋅32x−1, then dydx is equal to
- If y=ax2+b, then dydx at x=2 is equal to
Sample Questions
Ques. Explain (A) Limit (B) Discontinuity? (2 marks)
Ans: (A) Limit: Limit is a fundamental concept in calculus. It can be defined as the value of f(x) that the function approaches to some certain value of x.
(B) Discontinuity: When a function does not fulfill the conditions of a continuous function, it is termed as a discontinuity of a function. It can further be explained, as if a function is not continuous at every point in its domain, it is a discontinuous function.
Ques. What is Jump and Infinite Discontinuity? (2 marks)
Ans: Jump discontinuity: For any function f(x) at x = a, if both right-hand limit and left-hand limit exists but are not equal to one another, it is known as Jump discontinuity. It can be represented as, lim x -> h+ f(x) ≠ lim x -> h- f(x) Infinite Discontinuity: In this type of discontinuity, it can have one or more infinite limits. In such a case, the function diverges at x = a and get discontinuous
Ques. Explain the following question (A) Can we say that continuity guarantees differentiability (B)Can we say that differentiable means continuous? (2 marks)
Ans: (A) No, the implication of continuity is not differentiability. For example, the function ƒ: R → R defined by ƒ(x) = |x| happens to be continuous at the point 0. However, this function is not differentiable at the point 0.
(B) Any differentiable function shall be continuous at every point that exists its domain. Furthermore, a continuous function need not be differentiable. What this means is that differentiable functions happen to be atypical among the continuous functions.
Ques. Explain the following question (A)the concept of limit in continuity (B)the relationship between the concept of differentiability and the concept of continuity? (2 marks)
Ans: (A) A limit refers to a number that a function approaches as the approaching of the independent variable of the function takes place to a given value. For example, given the function f (x) = 3x, one can consider that the limit of f (x) as the approaching of x to 2 is 6. One can write this symbolically as f (x) = 6.
(B) The relationship between continuity and differentiability is that all differentiable functions happen to be continuous but not all continuous functions can be said to be differentiable.
Ques. What is the difference between continuity and differentiability? (3 marks)
Ans: The difference between continuity and differentiability are as follows:
| Continuity | Differentiability |
|---|---|
| Continuity for a function is given by limx -> a f(x) = f(a) | Differentiability for a function is given by f ' (x) = f (x + h) – f(x) / h |
| All continuous function are not said to be differentiable. | All differential function are said to be continous. |
| There is no gap in the graph of function. | The graph of differentiation function is equal to the slope of the graph. |
Ques. What are the conditions required for a function to be continuous? (3 marks)
Ans: The conditions required for a function to be continuous are as follows:
- The function f(x) specified at x = a, is continuous only if f(a) belongs to real number.
- The limit of the function as x approaches a, exists.
- The limit of the function as x approaches a, must be equal to the function value at x = a.
Ques. Show that f(x) is continuous at x = 5 for the function f(x) = (x2 – 2x)/ (x – 4)? (3 marks)
Ans: Given function f(x) = (x2 – 2x)/ (x – 4)
Substituting f(x) at x = 5, i.e., f(5) = (52 – 2(5))/ (5 – 4)
We get the answer as 15.
Since, we get the result as 15 for x = 5, i.e.,
f(5) = f(x)
Therefore, as the answer for both f(5) and f(x), appears to be the same, the function is considered as continuous.
Ques. Find the continuity of the function f(x) = 3x + 9 at the point x = 7? (3 marks)
Ans. The given function is f(x) = 3x + 4, and its value at the point x = 7 is f(7) = 30.
Let us find the limit of the function at the point x = 7.
Limx→7f(x)=Limx→7(3x+9)=3(7)+9=21+9=30=f(5)
Ques. Determine the points of discontinuity of the composite function y = f[f(x)], given that, f(x) = 1/x-2? (3 marks)
Ans: Given that, f(x) = 1/x-2
- We know that the function f(x) = 1/x-2 is discontinuous at x = 1
- Now, for x ≠1,
- f[f(x)]= f(1/x-2)
- = 1/[(1/x-2)-2]
- = x-2/ 4-x, which is discontinuous at the point x = 2.
- Therefore, the points of discontinuity are x = 1 and x=2.
Ques. Show that f(x) is continuous at x = 6 for the function f(x) = (x2 – 3x)/ (x – 5)? (3 marks)
Ans: Given function f(x) = (x2 – 3x)/ (x – 5)
Substituting f(x) at x = 6, i.e., f(6) = (62 – 2(6))/ (6 – 5)
We get the answer as 24.
Since, we get the result as 24 for x = 6, i.e.,
f(6) = f(x)
Therefore, as the answer for both f(6) and f(x), appears to be the same, the function is considered as continuous.
Ques. Find the continuity of the function f(x) = 4x + 12 at the point x = 10? (3 marks)
Ans. The given function is f(x) = 4x + 12, and its value at the point x = 10 is f(10) = 52.
Let us find the limit of the function at the point x = 10.
Limx→10f(x)=Limx→10(4x+12)=4(10)+12=40+12=52=f(10)
Check-Out:


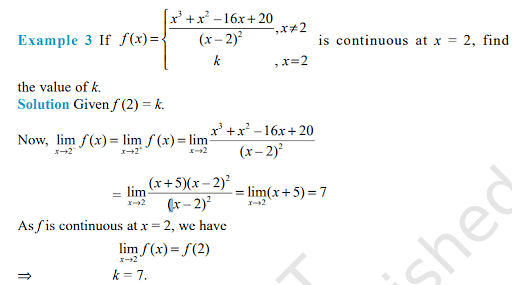





Comments