Slope Intercept Form Formula: Conversion and Examples

Slope of a line or straight line describes the direction (using the variables or axis X and Y) as well as the steepness of the line (means angle made at x-axis or theta. Hence, slope intercept form is one the ways to describe the slope of a straight line in mathematics. The slope of the straight line is represented by the variable ‘m’ and used in the equation y = mx+b.

Key Takeaways: Slope, Slope intercept form, One point slope form, Two point slope form, Straight line, Slope intercept

---

What is Slope Intercept Form?

[Click Here for Sample Questions]

Intercept means the straight line intersects a segment on the axis. 

Slope intercept form uses an equation to represent two things about a straight line passing through the X and Y axis:

• Direction of the straight line with the help of x and y variables
• Steepness of the straight line by using its slope ‘m.’ 

The equation of the slope intercept form is y = mx + b, where, m is the slope of the line and b is the y-intercept.

Discover about the Chapter video:

Continuity and Differentiability Detailed Video Explanation:

---

Slope Intercept Form: Formula Derivation

[Click Here for Sample Questions]

For finding the slope of a straight line, m, you have to divide the coordinate of the y-axis by the x-axis. Normally, while comparing two collinear points on a line, considering x₁,y₁ and x₂,y₂ is according to convention of how the equation has to be formed.

m = (y₂ – y₁)/(x₂ – x₁)

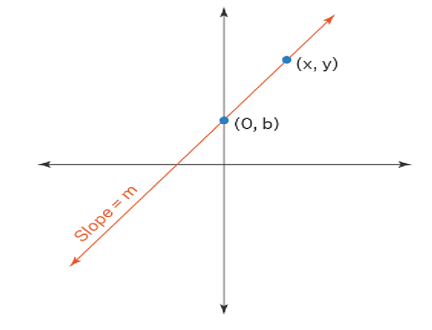
Slope Intercept Form Formula Derivation

Hence, let’s consider that the straight line intersects the y-axis at (0,b). It means that the 'b' or y-intercept in the equation of the line y = mx + b is the y-axis coordinate.

y – b = m (x – 0)

m = (y - b) / (x – 0)

⇒ m = (y – b) / (x)

Hence, 

mx = y – b

And, by rearranging we get, 

y = mx + b

Slope Intercept Form: General Equation of Straight Line

While the slope intercept form has the equation of y = mx + b and also called the general equation of straight line which is usually used, there is another method of representation that can be commonly found:

Ax + By + C = 0

Slope Intercept Form For A Straight Line: Intercept Form

Let’s take an example: Consider that a straight line passing through the x and y axis makes two intercepts, one on x-axis (a,0) and another on y-axis (0,b). 

Slope Intercept Form For A Straight Line Intercept Form

Thus, the intercept form of the straight line will be:

x/a + y/b = 1

Slope Intercept Form For A Straight Line: Normal Form

Let’s consider that there is a straight line. Now, if the length of the perpendicular drawn from the straight line to the origin is ‘p,’ and the angle made by the perpendicular with respect to the positive x-axis is α, therefore:

x cos É + y sinα = p

Slope Intercept Form For A Straight Line Normal Form

Slope Intercept Form For A Straight Line: One Point Form

The one point form or point form of slope of a straight line involves picking two points lying on the straight with coordinates (x₁,y₁) and (x₂,y₂). Then, instead of y = mx + c where the coordinates of only one point was used, replace them with the coordinates of two points like this: 

y = y₂ – y₁ and x = x₂ – x₁

Hence, the equation of the slope of a straight line according to one point form is:

y₂ – y₁ = m (x₂ – x₁) 

Slope Intercept Form For A Straight Line: Two Point Form

The two point form of slope of a line is quite simple. You only have to insert the equation of ‘m’ in the linear equation of one point form. The linear equation of a straight line according to one point form is y₂ – y₁ = m (x₂ – x₁).

y₂ – y₁ = {(y₂ – y₁) / (x₂ – x₁)} (x₂ – x₁)

Also Read:

---

Things to Remember

Following are some important points:

• The equation of a line represents the slope of the line and direction via x as well as y axis. 
• The equation of a straight line for slope intercept form is: y = mx + b. 
• The general equation of a straight line that can be rearranged is Ax + By + C = 0, where A, B, and C are real constants (A and B are non-zero). 
• Some more important formulas are:
  • m = (y₂ – y₁)/(x₂ – x₁)
  • One point form = y₂ – y₁ = m (x₂ – x₁) 
  • Intercept form = x/a + y/b = 1
  • Normal form = x cosÉ\(\Box\) + y sinα = p
  • Two point form = y₂ – y₁ = {(y₂ – y₁)/(x₂ – x₁)} (x₂ – x₁)

Also Read: