
Collegedunia Team Content Curator
Content Curator
Arctan is considered as the inverse tangent function in trigonometry. Inverse trigonometric functions usually occur by the prefix-arc. In mathematics, we represent arctan or the inverse tangent function as tan-1x. There are a total of 6 trigonometric functions, so there will also be six inverse trigonometric functions such as sin-1x, cos-1x, tan-1x, cosec-1x, sec-1x, cot-1x. Tan-1x is not the same as 1/tanx. This means that an inverse trigonometric function will not be reciprocal of the respective trigonometric function. The purpose of arctan is to find the value of an unknown angle by using the value of tangent trigonometric ratio.
| Table of Content |
Key Takeaways: Trigonometry, Ratio, Angles, Function, Identities, Inverse functions, Trigonometric functions,
Arctan Formulas
[Click Here for Sample Questions]
In a right-angle triangle, the “tan” of an angle describes the ratio of the “perpendicular/base”. The arctan of the ratio of “perpendicular/base” gives the value of an angle. Therefore, arctan is the inverse of “tan” function. If the tangent of θ is equal to x:
x = tan θ
θ = tan-1x
Here are some arctan formulas, identities that are used to solve simple as well as complicated sums on inverse trigonometry.
- θ = arctan(perpendicular/base)
- arctan(-x) = -arctan(x), for all x ∈ R
- tan (arctan x) = x, for all real numbers x
- arctan(x) = π/2 - arctan(x) = arccot(x), if x>0 or,
- arctan(x) = -π/2 - arctan(x) = arccot(x)-π, if x<0
- sin (arctan x) = x/√(1+x)2
- cos (arctan x) = 1/√(1+x)2
- arctan(x) = 2arctan(x/1+√1+x2)
- arctan(x) = ∫x0 1/z2+1 dz
We do have some formulas of arctan for π. Here are given below:
- π/4 = 4arctan (1/5) - arctan (1/239)
- π/4 = arctan (1/2) + arctan (1/3)
- π/4 = 2arctan (1/2) - arctan (1/7)
- π/4 = 2arctan (1/3) + arctan (1/7)
- π/4 = 8arctan (1/10) - 4arctan (1/515) - arctan (1/239)
- π/4 = 3arctan (1/4) + arctan (1/20) + arctan (1/1985)

Arctan Formula Graph
Read More:
Derivation of Arctan Formula
[Click Here for Sample Questions]
The derivation of arctan formula is as follows:
Let y = arctan x
Taking tan on both sides,
tany = tan (arctan x)
We already know that, tan (arctan x) = x,
Tan y = x
Now we will differentiate both sides we get,
dy/dx = 1/sec2y
According to the trigonometric identity sec2y = 1 + tan2y
dy/dx = 1/ (1 + tan2y)
On substitution, we get
d(arctan(x))/dx = 1/(1+x2)
Arctan Domain and Range
[Click Here for Sample Questions]
All of the trigonometric functions have a many-to-one relation. Hence, the inverse of function can only exist if it will be having a one-to-one and onto relation. In simple words, we can say that the trigonometric function must be restricted to its principal branch as we need only one value.
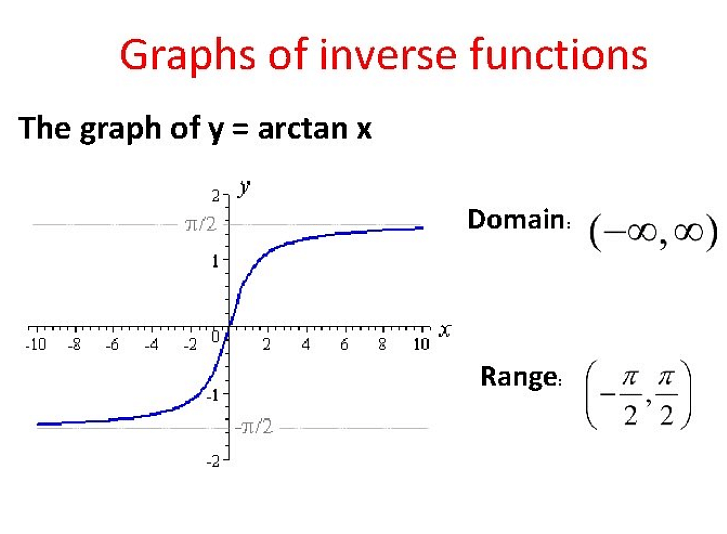
Domain and Range of Arctan
The domain of tanx is restricted to (-π/2, π/2). The range of tanx is always real numbers. The domain and range of trigonometric function converted into range and domain of inverse trigonometric function. Therefore, we can say that the domain of tan-1x are all real numbers and range is (-π/2, π/2).
Also Read: Difference between Variance and Standard Deviation
Integral of Arctan
[Click Here for Sample Questions]
The integral of arctan is the antiderivative of the inverse tangent function. Integration by parts is used to solve the integral of arctan.
Here, f(x) = tan-1x, g(x) = 1
The formula will be given as,
∫f(x)g(x)dx = f(x)∫g(x)dx - ∫[d(f(x))/dx * ∫g(x) dx] dx
On substituting the values and solving expression we will get the integral of arctan as,
∫tan-1x dx = xtan-1x - ½ ln|1+x2| + c
where, c is the constant of integration.
Properties of Arctan
[Click Here for Sample Questions]
Here are some properties of Arctan:
- tan(tan-1x) = x, for all real numbers x
- tan-1x + tan-1y = tan-1[(x+y)/(1 – xy)], if xy < 1
- tan-1x - tan-1y = tan-1[(x-y)/(1 + xy)], if xy> – 1
There are 3 properties for 2tan-1x:
- 2tan-1x = sin-1(2x/(1+x2)), when |x|≤1
- 2tan-1x = cos-1((1-x2)/(1+x2)), when x≥0
- 2tan-1x = tan-1(2x/(1-x2)), when -1<x<1
- tan-1(-x) = -tan-1x, for all x∈R
- tan-1(1/x) = cot-1x, when x>0
- tan-1x + cot-1x = π/2, when x∈R
- tan-1(tanx) = x, only when x∈R - {x:x = (2n+1) (π/2), where n∈Z} i.e. tan-1(tanx) = x only when x is not an odd multiple of π/2. Hence, tan-1(tanx) will be undefined.
Also Read: Decimal Expansion of Rational numbers
ArcTan Table
[Click Here for Sample Questions]
Any angle which is expressed in degrees can also be converted into radians. We should multiply the degree value by a factor of π/180. The arctan function takes a real number as an input and outputs the corresponding unique angle value. The table gives details of the arctan angle values for some real numbers.
| x | arctan(x) (in degrees) | arctan(x) (in radians) |
|---|---|---|
| - ∞ | -90° | -π/2 |
| -3 | -71.565° | -1.2490 |
| -2 | -63.435° | -1.1071 |
| -√3 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -1/√3 | -30° | -π/6 |
| -1/2 | -26.565° | -0.4636 |
| 0 | 0° | 0 |
| 1/2 | 26.565° | 0.4636 |
| 1/√3 | 30° | π/6 |
| 1 | 45° | π/4 |
| √3 | 60° | π/3 |
| 2 | 63.435° | 1.1071 |
| 3 | 71.565° | 1.2490 |
Things to Remember
- The integral of arctan is the antiderivative of the inverse tangent function. Integration by parts is used to solve the integral of arctan.
- Arctan is the reverse of tan. It can be used to calculate the value of an angle in a right-angled triangle using the tangent function.
- Tan-1x will exist if and only if we restrict the domain of tangent function.
- The basic formula for calculating arctan is given by θ = tan-1(perpendicular/base). Here, θ is the angle between the hypotenuse and base of the right-angled triangle.
- Arctan of infinity is the value of tan(π/2) = sin(π/2)/cos(π/2) = 1/0 = ∞. So, we can say arctan (∞) = π/2.
Also Read:
Sample Questions
Ques. Are arctan and cot the same? (2 Marks)
Ans. We cannot say that arctan and cot are the same because the inverse of tangent function is arctan given by tan-1x. However, cotangent is the reciprocal of the tangent function i.e. (tanx)-1 = 1/cotx.
Ques. Suppose we have a right-angled triangle with the dimensions, base = 1 unit, perpendicular = 1unit and hypotenuse = √2 units. Then, find the value of angle between the base and hypotenuse. (3 Marks)
Ans. As we know, tanθ = perpendicular/base. θ is the angle between the base and hypotenuse.
Thus, tanθ = 1/1 = 1
θ = tan-1(1)
θ = π/4
Value of the angle formed between the base and hypotenuse is π/4.
Ques. Solve: tan-1(1.732). (3 Marks)
Ans. From the given quantity, 1.732 can be written as a function of tan.
So, 1.732 = tan 60°
Hence, tan-1(1.732) = tan-1(tan 60) = 60°
60* = 60xπ/180
= 1.047 radians
Ques. In a right-angled triangle PQR, the base of which measures 17cm and height is 9cm. Determine the base angle. (3 Marks)
Ans. Base angle =?
Using arctan formula, θ = arctan (opposite ÷ adjacent)
θ = arctan (9 ÷ 7)
θ = arctan (0.52)
θ = 27.47 degrees
So, the angle is 27°.
Ques. What is the value of arctan 1/√3 in degrees? (3 Marks)
Ans. In the given triangle, the shortest side 1 is opposite to the smallest angle of 30* and the other adjacent side will have the length of √3.
The opposite-over-adjacent ratio of 30* will be exactly 1/√3, which means that the arctangent of the number is 30°.
tan-1(1/√3) = 30°.

Arctan 1/√3 in degrees
Ques. What are the uses of Arctan? (5 Marks)
Ans. The arctan is a trigonometric function and it is used to describe the values associated with the right-angled triangles. On a practical basis, we apply these functions in order to resolve the distance or height of the object which is complex to measure. It also has some practical applications in different fields like construction, architecture, landscaping, engineering, physics and other scientific areas.
We used to identify trigonometric functions by the sides of triangle that are used in the ratio of these formulas:
Sine = opposite/hypotenuse
Cosine = adjacent/hypotenuse
Tangent = opposite/adjacent
Ques. What is the value of arctan 1 in radians? (5 Marks)
Ans. In the given triangle, there are two equal sides which makes the tangent ratio of the acute angles equal to exactly 1.
As 180° = π rad, we have 45° = 180°/4 = π/4 rad.
This means that the arctangent of 1 as expressed in radians is equal to π/4.
If we want to calculate the value of -1, then the opposite and adjacent sides will be equal in length, corresponding to the angle π/4, but the tangent will be negative. As the solution will fall in the 4th quadrant, so it will be -π/4.

Arctan 1 in radians
Ques. How and why do we use the inverse of trigonometric functions? (5 Marks)
Ans. We use the inverse trigonometric functions in order to resolve the angle measures when we are aware of the sides of the triangle. Furthermore, we can also use it to decide the measure of an angle when we know the side opposite and the side adjacent to the angle.
A good approach to use the arctan is the scientific calculator. We can trace the button that’s just above the tangent on the calculator. Furthermore, we can also use a data table to resolve arctan, but this can be an exhaustive and lengthy method, therefore, it will be most feasible if we don’t have a scientific calculator.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments