Secant Function: Meaning, Properties, Graph

Secant function is the reciprocal of the cosine function in general. Other than the secant function, there are other similar reciprocal functions in the mathematical domain of Inverse Trigonometric Functions. For instance, cotangent is considered the reciprocal function of the tangent function, while cosecant is the reciprocal of sine, as per their trigonometric values.

Key Takeaways: Secant function, secθ, reciprocal, Trigonometry, domain, range, tangent function, trigonometric functions, trigonometric values, coordinate plane

Meaning of Secant Function

[Click Here for Sample Questions]

The secant function is the reciprocal of cosine. A reciprocal function is often defined as the reciprocal or otherwise known as the multiplicative inverse of another function. Now, when considering that −1 ≤ cos x ≤ 1, it is clear that y = sec x does not involve values which are in (−1, 1). In reference to a coordinate plane, it can be said that the secant function is considered as r/x.

In a nutshell, secant function has a range of (−∞,1] ∪[1, ∞). As per the function, y = sec, which is x = 1/cosx. Commonly, the function is defined for every value of x, with an exclusion of when cos x = 0. By and large, this means that y = sec x has a domain of . R\ {(2n + 1) \(\frac{\pi}{2}\) : n ∈ Z}

The secant function is an even function. Typically, it has been found that the secant function neither has a maximum or a minimum value limit. It is because the secant function is periodic, with a period value of 2π. The secant function or sec function, in a right-angled triangle, can otherwise also be described as the ratio of the length of the hypotenuse to the length of the base.

The secant function (commonly abbreviated to sec) is often also defined as the distance one point to another (O and M in the image illustrated below). By establishing the relation between sec (θ) and cos (θ), it can be said that, sec (θ) = r/x = 1/cos (θ)

It is important to highlight that,

Secant function sec(θ) is defined as:

Sec(θ) = r/x = 1/Cos(θ)

Also Note that,

1. sec(θ + 2π) = \(\frac{1}{cos (\theta + 2 \pi)} = \frac{1}{cos (\theta)}\)= sec(θ)

and therefore sec(θ) is a periodic function whose period is equal to 2π.

Secant Function

Also Read: Direction Cosines

Properties of Secant Function

[Click Here for Sample Questions]

As much as other trigonometric functions, the secant function can be depicted in the form of a line segment that is associated with the unit circle. If expressed in reference to cosine, it can be said that sec (θ) = 1/ cos (θ). The degree and value of the secant function is illustrated below.

Properties of Secant Function

The properties of the secant function can only be determined by the quadrant it typically lies in. The quadrant can be illustrated as,

Properties of Secant Function

Here are the properties of the Secant function:

• Sec x has a period value which is typically equal to 2π. A periodic function can be defined as a function that consequently results as a function that is equal to the original one, during its meet with a particular horizontal shift, say – much like f (x+P)=f(x).
• Sec x has been found to have vertical asymptotes at every value associated to x = π/2 + nπ, wherein n is an integer of any class.
• The secant function has a range of (−∞,1] ∪[1, ∞).
• Usually, the domain of the secant function is found to be the set of every real number, with an exclusion of x = π/2 + nπ, wherein n is an integer of any class.
• The secant function is usually considered as an even function because sec(x)=sec(−x).

Also Read: Trigonometry Ratio Identity

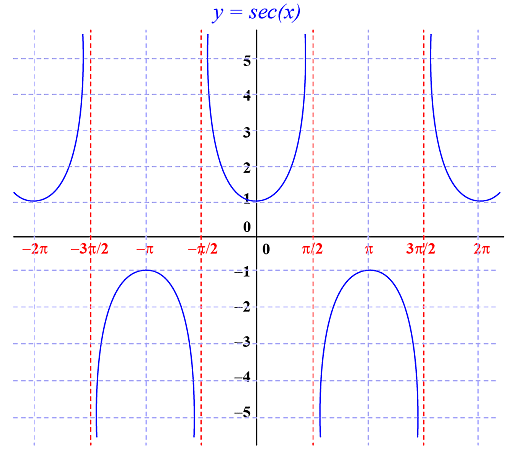
Graph of Secant Function

[Click Here for Sample Questions]

Cosine is often depicted by the x coordinate geometry of the point P (which is the point where the terminal side of an angle θ is found bisecting the circle’s circumference), we can deduce that, Sec (θ) = 1/x.

Now, the graph of the secant function in 0 ≤ x ≤ 2 π, wherein x ≠ π/2, 3π/2, can plotted as,

Graph of Secant Function

If you notice in the image above, the first and fourth quadrants (interval of – π/2 < x < π/2), y = sec x are found to consider positive values alone. Quite naturally, it considers the negative values only in the second and third quadrants, also otherwise denoted by the interval of π/2 < x < 3π / 2.

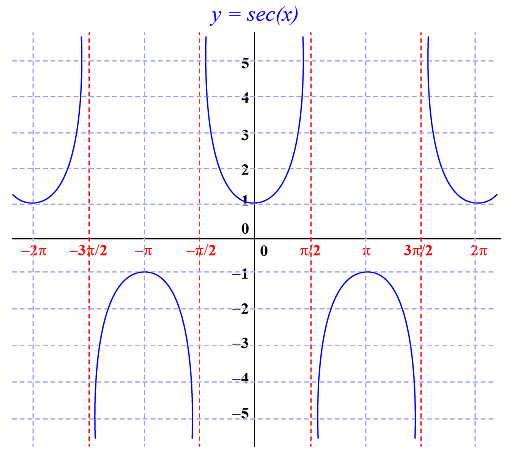
The image below represents a unit circle that has a centre O, alongside a point P. It makes an angle of OP.

Graph of Secant Function

As we already know, sec x = 1/cos x. It can be noted that, Sec x = OP/OQ = 1/OQ.

When x varies, the value of sec x is typically also seen to change with the following variation of length, OQ. The derivation of sec x becomes feasible when determining 1/y, for every value of y on the curve made of y = cosx. Plotting the graph, we get,

Graph of Secant Function

Also Read:

Things to Remember

Following are some important points:

• The secant function is basically the reciprocal of cosine.
• The absolute value of cosine of a typical angle can never really surpass one, which also means that the reciprocal of it will never be less than one as well.
• Sec x has a period value typically equal to 2π.
• The relation between sec (θ) and cos (θ) can be represented by sec (θ) = r/x = 1/cos (θ)

Also Read: Sin 180 Degrees Value and Derivation