
Namrata Das Exams Prep Master
Exams Prep Master
Continuous function is a function in mathematics that is continuous and does not have any discontinuities in its expected range of values. Continuous functions are a very important concept in the understanding of calculus. Moreover, a continuous function is applied in almost every function to ensure small changes in their values. A continuous function is said to be continuous at a fixed point if a graph can be plotted for the function, around that point, without the pencil leaving the graph paper for once that is, the graph can be plotted without any discontinuities. A function that is not continuous is known as a discontinuous function. Let’s have a look at the topic and discuss some important questions.
Read more: Continuity and Differentiability
| Table of Content |
Key Takeaways: Continuous function, calculus, discontinuities, discontinuous function, fixed point, limit, certain point, function
Continuous Function Definition
[Click Here for Sample Questions]
The definition for a continuous function in mathematics is given below-
A function, say f(x) is said to be continuous at a certain point, suppose, x=a if it follows the following points. These are-
- f(a) exists
- lim x→a f(x) exists and
- lim x→a f(x) = f(a)
The rule number 2 can also be written as lim x→a- f(x) = lim x→a+ f(x). These three rules define the continuity of a function i.e. a function that has a continuous graph without any break points at point x=a, the following statements have these meanings
- If lim x→a f(x) exists, it means the function should be of the same value from the left side of the point and the right side of the point x=a i.e. lim x→a- f(x) = lim x→a+ f(x).
Read more: Mean Value Theorem

Graph depicting lim x→a- f(x) Graph depicting lim x→a+ f(x)
- limx→a f(x) = f(a) says that the function f(a) is the same as the limit of the function at the point x=a.

Graph depicting limx→a f(x) = f(a)
Thus, if these graphs are combined together, the resulting graph would obey all the conditions that are required for a function to be continuous. The resulting graph is-
Read more: Rolle’s Theorem

Thus, lim x→a f(x) = f(a) suggests that function f(x) is continuous at point x=a.
A function needs to be continuous in calculus if it is differentiated, since only continuous functions are differentiable. The functions that do not follow these conditions are called discontinuous functions. A function that is continuous at a certain point does not have any breaks or follows continuity at that point. A function that is continuous over an interval has to display continuity at each and every point in the interval i.e. the graph of that function cannot break or jump at any point in that interval.
Discover about the Chapter video:
Continuity and Differentiability Detailed Video Explanation:
Also Read:
Properties of Continuous Function
[Click Here for Sample Questions]
A continuous function has a number of properties that holds the continuity of that function. Those properties are listed below. If there are two continuous functions f(x) and g(x) at point x=a, then
- The functions f + g, f - g, f.g are also continuous at x=a. The function f/g is also continuous at point x=a given that g(a) ≠ 0.
- All the polynomial functions and the absolute function |x| are continuous over a set of all real numbers.
- The exponential functions are also continuous for all real numbers.
- The logarithmic functions such as log x, ln x, and √x are all continuous in their respective domains.
- The functions sin x and cos x are continuous for all real numbers, while the functions tan x, cosec x, sec x, and cot x are all continuous in their respective domains according to trigonometry.
- If f is a function continuous at g(a), then their composition function i.e. f o g will also be continuous at x=a.
Read more: Quotient Rule
Theorems based on Continuous Functions
[Click Here for Sample Questions]
- Theorem 1: All polynomial functions are continuous on (-∞,∞).
- Theorem 2: The functions ex, sin x, cos x, and arctan x are continuous on (-∞,∞).
- Theorem 3: If two functions f and g are continuous on an interval [a, b], then f+g, f-g, and fg are continuous on [a, b]. But f/g is continuous on [a, b] given that f/g is not equal to zero anywhere in that interval.
Read more: Euler’s Number
Examples of Continuous Functions and Graphical Representation
[Click Here for Sample Questions]
- Examples of Continuous Functions
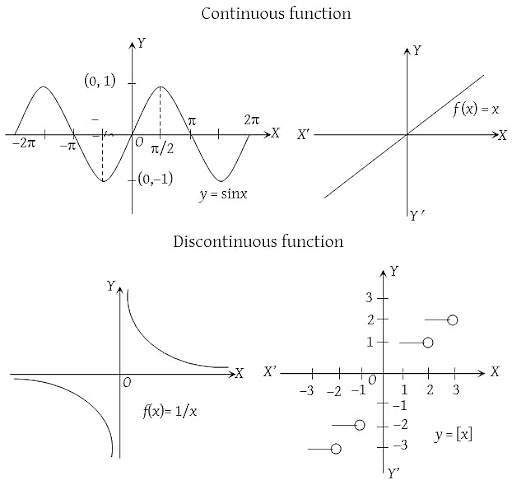


Read more: inverse trigonometric functions

Read more: method of solving a differential equation
Things to Remember
- A function f(x) is said to be continuous at a certain point x=a if it follows the following points. These are-
- f(a) exists
- lim x→a f(x) exists and
- lim x→a f(x) = f(a)
- The functions that do not follow the conditions for continuity are called discontinuous functions.
- The functions f + g, f - g, f.g are also continuous at x=a. The function f/g is also continuous at point x=a given that g(a) ≠ 0. If f is a function continuous at g(a), then their composition function i.e. f o g will also be continuous at x=a.
- If limx→a f(x) exists, it means the function should be of the same value from the left side of the point and the right side of the point x=a i.e. lim x→a- f(x) = limx→a+ f(x).
- The exponential functions are continuous for all real numbers.
- The logarithmic functions such as log x, ln x, and √x are continuous in their respective domains. The functions sin x and cos x are also continuous for all real numbers, while the functions tan x, cosec x, sec x, and cot x are all continuous in their respective domains.
- A function that is continuous over an interval has to display continuity at each and every point in the interval i.e. the graph of that function cannot break or jump at any point in that interval.
- A continuous function is said to be continuous at a fixed point if a graph can be plotted for the function, around that point, without the pencil leaving the graph paper for once, that is, the graph can be plotted without any discontinuities.
Read more: Differentiation and Integration Formula
Sample Questions
Ques. What are 3 Conditions for the Continuity of a Function? [2 marks]
Ans. A function f(x) is continuous at a certain point x=a only if it follows the following conditions.
- f(a) exists
- limx→a f(x) exists and
- limx→af(x) = f(a)
The second condition can also be written as lim x→a- f(x) = lim x→a+ f(x).
Ques. Find the relation between a and b if the following function is continuous at x = 4.
f(x) = { ax − 3,if x ≤ 4bx+8,if x>4
ax − 3, if x≤4bx+8, if x>4 [3 marks]
Ans. Here, f(x) is a continuous function at x = 4. By continuous function equation,
lim x→4- f(x) = lim x→4+ f(x) = f(4)
lim x→4 (ax - 3) = lim x→4 (bx + 8) = a(4) - 3
Thus, b(4) + 8 = a(4) - 3
From the first two expressions,
4a - 3 = 4b + 8
4a - 4b = 11
Therefore, the relation between a and b is 4a - 4b = 11.
Ques. What are piecewise functions? [2 marks]
Ans. A piecewise function is a form of continuous function where the function is defined differently in separate intervals. One example of piecewise function is-

Ques. Prove that the following function is NOT continuous at x = 2 and verify the same using its graph. Also, mention the type of discontinuity.
f(x) = {x−3, if x ≤ 2,
{8, if x > 2 [3 marks]
Ans. It is given that a = 2.
The given function is a piecewise function. Thus, we have to find the left-hand and the right-hand limits separately. Note that
- x → 2-
or, x < 2
or, f(x) = x - 3 and
- x → 2+
or, x > 2
or, f(x) = 8.
Calculating the limits now.
lim x→2- f(x) = lim x→22 (x - 3)
= 2 - 3 = -1
lim x→2+ f(x) = lim x→2 8 = 8
Here, lim x→2- f(x) ≠ lim x→2+ f(x).
Thus, lim x→2+ f(x) does not exist and hence f(x) is not continuous at x = 2.
Ques. Show that every polynomial function is continuous. [3 marks]
Ans. A function p is a polynomial function if it is defined by
p (x) = a + ax + … +anxn for some natural number n, a ≠ 0 and ai ∈ R.
Which indicates that this function is defined for every real number. Now, for a fixed real number c, we have
lim x→c p(x) = p(c)
On comparing this equation with the condition for continuity of a function,
lim x→a f(x) = f(a)
we know,
p is continuous at c and since c is any real number, p is continuous at every real number and hence p is a continuous function.
Ques. Discuss the continuity of sine function. [3 marks]
Ans. We know from the sine graph,
lim x→0 sin x = 0
Now, f (x) = sin x is defined for every real number.
Let c be a real number and let x = c + h. If x→c, we know that h → 0.Therefore
lim x→c f(x) = lim x→c sin x
- = lim h→0 sin (c+h)
- = lim h→0 [sin c cos h + cos c sin h]
- = lim h→0 [sin c cos h] + lim h→0 [cos c sin h]
= sin c + 0 = sin c = f (c)
Thus lim x→c f (x) = f (c) and hence f is a continuous function.
Thus, sine is a continuous function, proved.
Ques. Find all the points of discontinuity of the function f defined by
f(x) = { x + 2 , if x ≤ 1; x - 2, if x > 1 [3 marks]
Ans. The given function f is defined in every point of the real line.
Let c be a real number and
Case 1
If c < 1, then f(c) = c + 2.
Therefore, lim x→c f (x) = lim x→c (x + 2) = c + 2
Therefore, f is continuous for all real numbers less than 1 i.e. for x<1.
Case 2
If c > 1, then f(c) = c - 2.
Therefore, lim x→c f(x) = lim x→c (x–2) = c - 2 = f(c)
Thus, f is continuous for all real numbers greater than 1 i.e. for x>1.
Case 3
At c = 1,
The left hand limit of f at x = 1 is given by,
lim x→1- f (x) = limx→1- (x + 2) = 1 + 2 = 3
The right hand limit of f at x = 1 is
limx→1+ f(x) = lim x→1+ (x - 2) = 1 - 2 = -1
Thus, the values of the left-hand limit and right-hand limit are not the same, therefore, f at x=1 is not continuous.
Hence, for functions where x > 1, and x < 1 are continuous, the point of discontinuity of the function is at x=1.
Ques. Discuss the continuity of the function f given by f (x) = x3 + x2 - 1. [2 marks]
Ans. The given function f is defined in every point of the real line.
Let c be a real number and the value of f at c is c3 + c2 - 1.
We also know that,
lim x→c f(x) = lim x→c (x3 + x2 - 1) = c3 + c2- 1
Since on substitution of a value both expressions have the same value.
Thus limx→c f (x) = f (c), and hence f is continuous at every real number. This means
f is a continuous function.
Ques. Check the continuity of the function f given by f(x) = 3x + 2 at x = 1. [2 marks]
Ans. Given,
f(x) = 3x + 2
Now substituting x = 1 in f(x), we get,
f(1) = 3(1) + 2
= 3 + 2 = 5
Thus, the function is defined at the given point x = 1 and its value is 5.
Now, we have to find the limit of the function at x = 1.
lim x→1 f(x)=limx→1 (3 x + 2)
= 3(1) + 2 = 5
which is the same value as f(1).
Thus, the given function f(x) = 3x + 2 is continuous at x = 1.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments