Cosine Function: Trigonometric Identities, Properties & Graphs

Cosine is one of the primary mathematical trigonometric ratios. Cosine function is defined as the ratio of lengths of sides adjacent to the angle and hypotenuse of a right-angled triangle. Mathematically, the cosine function formula in terms of sides of a right-angled triangle is written as: cosx = adjacent side/hypotenuse = base/hypotenuse, where x is the acute angle between the base and the hypotenuse.

Cosine Function

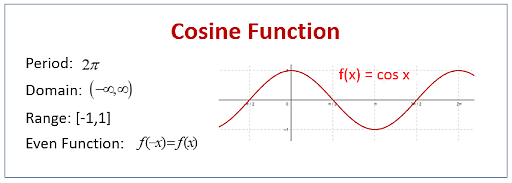
It is denoted by cosx, where x is the angle. Cosx is a periodic function and has a period of 2π. The cosine function is used to show some real-life scenarios such as radio waves, tides, sound waves, electric currents, musical tones etc.

Read More: Introduction to Trigonometry

Key Terms: Cosine Function, Cosine function identities, Cosine Function Graph, Cosine Values Table, Cos, triangle, Circle, Horizontal axis, Acute angle

---

Cosine Function

[Click Here for Sample Questions]

Let’s consider a unit circle which is centred at the origin of the coordinate plane. A point P moves to the circumference of the circle. From the given figure, we will observe that P is present in the first quadrant and OP makes an acute angle of x radians with the positive x axis. PQ is a perpendicular drop from P to the horizontal axis. Then, a triangle is formed by joining the points O, P and Q where QO is the base, PQ is the height of the triangle. The cosine formula for the above condition will be written as: cosx = OQ/OP. Here, x is the acute angle which is formed between the base and hypotenuse.

 

Cosine function from unit circle

Also Read: Applications of Trigonometry

---

Cosine Function Identities

[Click Here for Sample Questions]

In trigonometry, there are some identities which are used to solve various maths problems involving the cosine function. These are:

• cosx = 1/secx
• cos^-1x = arccos x where x lies between [-1, 1]
• sin²x + cos²x = 1
• cos(x+y) = cosx cosy - sinx siny
• cos(x-y) = cosx cosy + sinx siny
• cos2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
• Derivative of cosx: d(cosx)/dx = -sinx
• Integral of cosine function: ∫cosx dx = sinx + c, where c is the constant of integration

Read More: Ratios and Identities in Trigonometry

---

Properties of Cosine Function

[Click Here for Sample Questions]

Cosine function is a special trigonometry function which has different properties. Some of them are listed below:

• cosx is an even function because cos(-x) = cosx
• The reciprocal of the cosine function is the secant function.
• The domain of cosine function is real numbers and range is [-1, 1].
• The graph of cosx repeats itself after 2π, so the function is periodic with a period of 2π. 
• The power series expansion of cosine function is cos x = ∑^∞_n=0(-1)ⁿ x²ⁿ/(2n)!

Read More: Domain and Range of Trigonometric Function

---

Graph of Cosine Function

[Click Here for Sample Questions]

From the above image shown, we note that cosx = OQ/OP = OQ/1 = OQ. Due to the variation of x, the value of cosine also varies with variation in the length of OQ. Following are some cases of the variation:

Cosine Function Variations

Case 1: Variation of OQ in the first quadrant

Suppose that initially, P is on the horizontal axis. Let’s considering movement of P through 90° or π/2 rad. OQ has decreased in length from an initial value of 1 (if value of x is 0 rad) to a final value of 0 (if value of x is π/2 rad). 

Case 2: Variation of OQ in second quadrant

In this case, P moves from 90° position to 180° position. In this phase, the length of OQ increases, and value of cosine has decreased from a value of 0° at 90° to a minimum of -1 at 180°.

Read More: Value of log1 to 10

Case 3: Variation of OQ in third quadrant

In this case, P moves from 180° to 270° so the length of OQ decreases. Since the direction is along the negative y-axis, the actual value of cosx increases from -1 to 0. So, the value of cosine for angle x increases. 

Case 4: Variation of OQ in fourth quadrant

In this case, P moves from 270° to 360°, so OQ increases from 0 to 1. The length of OQ increases with the algebraic value of OQ increasing. So, the value of cosine for angle x increases.

These variations can be plotted on a graph. The horizontal axis represents input variable x as angle and vertical axis represents value of cosine function for x. So, the graph is plotted as shown below:

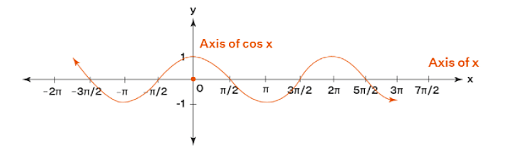
Cosine Function Graph

Read More: Differentiation and Integration Formula

---

Things to Remember

• We can write the cosine function mathematically as: cosx = base/hypotenuse. 
• Cosine is a periodic function with a period of 2π. Domain of cosx is (-∞, ∞) with the range [-1, 1]. 
• The graph of cosine helps in finding out the average daily temperature of any location. It is similar to that of a sine graph. 
• The main difference between sine and cosine graphs is that sine graph starts from 0 whereas the cos graph begins from 90°.
• The cos graph generally starts from 1 and falls till -1 and then starts to rise again. This movement gives an up and down curve. 
• Trigonometry functions and values always deal with the relation to the right-angled triangle. Aviation, Criminology, Marine biology and navigation etc make use of Trigonometry in every aspect.

Also Read: