
Content Curator
A parabola is a set of points in a plane forming a U-shaped curve such that all these points are equidistant from a fixed point, focus and a fixed-line, directrix. All the rays parallel to the axis of the symmetry that strike the concave surface of the parabola are reflected from its focus.
| Table of Content |
Keyterms: Parabola, Plane, Curve, Hyperbola, Vetrex, Ellipse, Coordinate point, Symmetry, Latus rectum, Focal Chord
Read Here: Angle Between Two Lines
Parabola: Important Terms
[Click Here for Sample Questions]
There are several important terms and concepts associated with Parabolas. Some of them are:
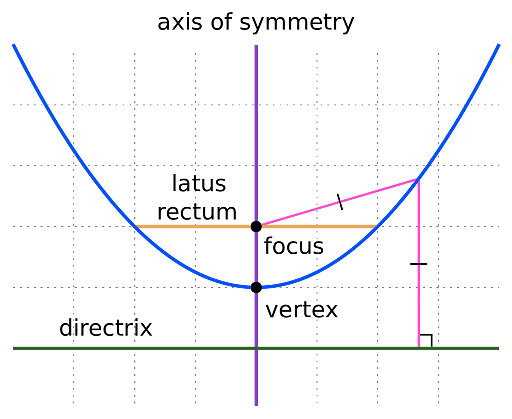
Axis of symmetry: The axis of symmetry is the line passing through the centre of the parabola via its focus and vertex and is perpendicular to the directrix. It also divides the graph of a parabola into two equal parts.
Vertex: Vertex is the point of intersection of the parabola and the axis of symmetry. It is a coordinate point on the parabola from where it takes its sharpest turn.
Parabola
Directrix: The directrix is a fixed-line not touching the parabola such that the distance between any point on the parabola and its focus is equal to the distance between that point and the directrix. It is perpendicular to the axis of symmetry.
Focal Chord: Any chord that passes through the focus of the parabola is called the focal chord.
Latus Rectum: A focal chord parallel to the directrix is called the latus rectum.
Length of the latus rectum = 4a
Discover about the Chapter video:
Conic Sections Detailed Video Explanation:
Read Here: Conic Sections
Standard Equations of Parabola
[Click Here for Previous Year Questions]
There are four forms of a parabola. The standard equations of the parabola with the given coordinates of vertices, foci and equation of directrix are as follows:
- Vertex: (0, 0)
Focus: (a, 0)
Directrix: x = -a
Equation of parabola: y2 = 4ax
Parametric Coordinates: (at2, 2at)
- Vertex: (0, 0)
Focus: (-a, 0)
Directrix: x = +a
Equation of parabola: y2 = -4ax
Parametric Coordinates: (-at2, 2at)
- Vertex: (0, 0)
Focus: (0, a)
Directrix: y = -a
Equation of parabola: x2 = 4ay
Parametric Coordinates: (2at, at2)
- Vertex: (0, 0)
Focus: (0, -a)
Directrix: y = a
Equation of parabola: x2 = -4ay
Parametric Coordinates: (2at, -at2)
where, -∞ < t < ∞

Standard Equations of Parabola
Parabola: Important Observations
[Click Here for Sample Questions]
- If the equation of parabola includes the term y2, then the axis of symmetry is along the X-axis. And if the equation of parabola includes the term x2, then the axis of symmetry is along the Y-axis.
- When the axis of symmetry is along the X-axis,
- if the coefficient of x is positive, then the parabola opens to the right.
- if the coefficient of x is negative, then the parabola opens to the left.
- When the axis of symmetry is along the Y-axis,
- if the coefficient of y is positive, then the parabola opens upward.
- if the coefficient of y is negative, then the parabola opens downwards.
Check Now: Introduction to Three Dimensional Geometry
Position of a Point with Respect to a Parabola
[Click Here for Previous Year Questions]
Let us consider the standard equation y2 = 4ax for the parabola.
y2 = 4ax
S = y2 - 4ax = 0

Position of a Point with Respect to a Parabola
If the point is (x1, y1), then S1 = y12 – 4ax1
- For S1 < 0, the point is inside the curve.
- For S1 = 0, the point is on the parabola.
- For S1 > 0, the point is outside the curve.
Also Read:
| Related Articles | ||
|---|---|---|
| Eccentricity of Ellipse | Latus rectum of Ellipse | Ellipse |
| Latus rectum of Hyperbola | Eccentricity | Locus |
Things To Remember
- A set of points on a plane forming a U-shaped curve such that all these points are equidistant from a fixed point and a fixed-line called the focus and directrix respectively is called a parabola.
- The standard equation of the parabola is of the form, y2 = 4ax, y2 = -4ax, x2 = 4ay or x2 = -4ay.
- The length of the latus rectum of the parabola is 4a.
- A vertex is the point of intersection of the parabola and its axis of symmetry.
Previous Year Questions
- The length of the common chord of the ellipse…..[BITSAT 2007]
- The tangents drawn at the extremeties of a focal chord of the parabola...[KCET 2008]
- The equations of the two tangents from (-5, - 4) to the circle...[KCET 2012]
- The eccentricity of the ellipse...[KCET 2007]
- The length of transverse axis is equal to...[KCET 2015]
- Two circles centered at (2, 3) and (5,6) intersect each other...[KCET 2010]
- Equation of the circle centered at (4, 3) touching the circle….[KCET 2010]
- The points (1,0),(0,1),(0,0) and (2k, 3k) =0 are concyclic if k = _____[KCET 2010]
- The locus of the point of intersection of the tangents drawn at the ends of a focal chord of the parabola….[KCET 2010]
- For the parabola y2=4x, the point P whose focal distance is 17, is….[KCET 2009]
Sample Questions
Ques. For parabola y2 = 16x, find the coordinates of the focus, the length of the latus rectum and the equation of directrix. (3 marks)
Ans. The given equation of the parabola is of the form y2 = 4ax.
Comparing it with the standard equation, we get
4a = 16
a = 4
Coordinates of focus: (a, 0) = (4, 0)
The length of the latus rectum: 4a = 16
Equation of directrix: x = -a = -4
So, the coordinates of the focus are (4, 0), the length of the latus rectum is 16 and the equation of directrix is x = – 4.
Ques. If the coordinates of the focus are (0, 5) and the equation of directrix is y = – 5, then find the equation of the parabola. (3 marks)
Ans. The coordinates of the focus are of the form (0, a) and the equation of directrix is of the form y = -a. The focus is on the y-axis and the axis of symmetry is the y-axis.
So, the parabola is of the form x2 = 4ay.
Here, a = 5.
So, x2 = 4ay = 4 x 5y = 20y
Hence, the equation of the parabola is x2 = 20y.
Ques. If the vertex of the parabola is at the origin and its focus has coordinates (0, -3), then find the equation of the parabola. (3 marks)
Ans. Here, the vertex is at the origin and the coordinates of the focus are of the form (0, -a). The focus is on the y-axis and the axis of symmetry is the y-axis.
So, the parabola is of the form x2 = -4ay
With a = 3, x2 = -4ay = -4 x 3y = – 12y
The equation of the parabola is x2 = – 12y.
Ques. Find the length of the latus rectum of the parabola x2 = – 8y. (2 marks)
(a) 4
(b) 32
(c) 8
(d) 16
Ans. The length of the latus rectum of the parabola is 4a.
From the given equation of parabola, with the standard equation x2 = -4y, 4a = 8.
Hence, the length of the latus rectum is 8.
Ques. Find the distance of focus from the vertex of the parabola x2 = 20y. (3 marks)
(a) 4
(b) 5
(c) 2
(d) 10
Ans. The given parabola is of the form, x2 = 4ay.
4a = 20
a = 5
And the coordinates of vertex and focus are (0, 0) and (0, a) respectively. So, the distance between them is a = 5.
Ques. Given that the equation of a parabola is y2- 4x- 4y=0, Calculate the vertex, focus, directrix of the parabola. (4 marks)
Ans. Re-arranging the above equation, we get:
y2 – 4y=4x
Adding y on both sides, we get: y2 - 4y + 4 = 4x + 4
So, (y-2)2 = 4(x+1)
Let Y = (y-2) and X = (x+1)
So, we get: Y2 = 4X
Comparing with the standard form: y2 = 4ax,
a = 1
The vertex (according to X and Y) will be (0,0)
Since X=(x+1) and Y=(y-2)
Vertex = (x+1, y-2)
According to the new axis, focus is (1,0)
Hence, Since X=(x+1) and Y=(y-2)
Focus = (0,2)
Equation of directrix according to the new axis is X= – 1
since X = x+1
x = – 1 is the equation of directrix
Ques. Given that the vertex and focus of parabola are (-2, 3) and (1, 3) respectively, find the equation of the parabola. (3 marks)
Ans. Since the vertex is (-2, 3)
the equation becomes: (y-3)2 = 4a(x+2)
Also, a = abissca of focus – abissca of vertex
So, a = 1-(-2) = 3
Hence, equation of parabola = (y - 3)2 = 4 . 3(x + 2)
Simplifying this equation,
y2 - 6y - 12x = 15.
Also read:





Comments