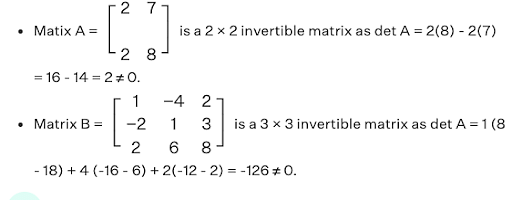Find the inverse of each of the matrices,if it exists. \(\begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix}\)
Approach Solution - 1
Let A=\(\begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix}\)
We know that \(A = IA\)
⇒ \(\begin{bmatrix} 2 & 3\\ 5 & 7 \end{bmatrix}\) = \(\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}A\)
⇒ \(\begin{bmatrix} 1 & \frac32\\ 5 & 7 \end{bmatrix}\)=\(\begin{bmatrix} \frac12 & 0\\ 0 & 1 \end{bmatrix}\)\(A\) \((R_1 \rightarrow (\frac{1}{2}R_1) )\)
⇒ \(\begin{bmatrix} 1 & \frac32\\ 0 & \frac{-1}{2} \end{bmatrix}\)= \(\begin{bmatrix} \frac12 & 0\\ -\frac{5}{2} & 1 \end{bmatrix}A\) \( (R_2→ R_2-5R_1) \)
⇒ \(\begin{bmatrix} 1 & 0\\ 0 & \frac{-1}{2} \end{bmatrix}\)\(=\begin{bmatrix} -7 & 3\\ -\frac{5}{2} & 1 \end{bmatrix}A\) \((R_1→ R_1+3R_2)\)
⇒ \(\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\) = \(\begin{bmatrix} -7 & 3\\ 5 & -2 \end{bmatrix}A\) \((R_2\rightarrow-2R_1)\)
\(A^{-1}\)= \(\begin{bmatrix} -7 & 3\\ 5 & -2 \end{bmatrix}\)
Approach Solution -2
\(\mathbf{A} = \begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix}\)
we use the formula for the inverse of a \(2 \times 2\) matrix:
\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\)
where \(\mathbf{A} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\) and \(\det(\mathbf{A}) = ad - bc\).
First, we calculate the determinant \(\det(\mathbf{A})\):
\(\det(\mathbf{A}) = (2)(7) - (3)(5) = 14 - 15 = -1\)
Since the determinant is not zero, the inverse exists. Now, we apply the formula for the inverse:
\(\mathbf{A}^{-1} = \frac{1}{\det(\mathbf{A})} \begin{bmatrix} 7 & -3 \\ -5 & 2 \end{bmatrix}\)
Substituting \(\det(\mathbf{A}) = -1\):
\(\mathbf{A}^{-1} = \frac{1}{-1} \begin{bmatrix} 7 & -3 \\ -5 & 2 \end{bmatrix} = \begin{bmatrix} -7 & 3 \\ 5 & -2 \end{bmatrix}\)
So, the answer is \(\begin{bmatrix} -7 & 3 \\ 5 & -2 \end{bmatrix}\).
Top Questions on Matrices
- Let
\(M=\begin{pmatrix} 0 & 0 & 0 & 0 & -1 \\ 2 & 0 & 0 & 0 & -4 \\ 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 3 \\ 0 & 0 & 0 & 2 & 2 \end{pmatrix}\)
If p(x) is the characteristic polynomial of M, then p(2) - 1 equals _________ - Consider the 4 × 4 matrix
\(M = \begin{pmatrix} 0 & 1 & 2 & 3 \\ 1 & 0 & 1 & 2 \\ 2 & 1 & 0 & 1 \\ 3 & 2 & 1 & 0 \end{pmatrix}\)
If ai,j denotes the (i, j)th entry of M-1 , then a4,1 equals __________ (rounded off to two decimal places). - For a matrix M, let Rowspace(M) denote the linear span of the rows of M and Colspace(M) denote the linear span of the columns of M. Which of the following hold(s) for all A, B, C ∈ M10(\(\R\)) satisfying A = BC ?
- Let \(a=\begin{bmatrix} \frac{1}{\sqrt3} \\ \frac{-1}{\sqrt2} \\ \frac{1}{\sqrt6} \\ 0\end{bmatrix}\). Consider the following two statements.
P : The matrix I4 - aaT is invertible.
Q: The matrix I4 - 2aaT is invertible.
Then, which one of the following holds ? - Let A be a 6 × 5 matrix with entries in ℝ and B be a 5 × 4 matrix with entries in ℝ. Consider the following two statements.
P : For all such nonzero matrices A and B, there is a nonzero matrix Z such that AZB is the 6 × 4 zero matrix.
Q : For all such nonzero matrices A and B, there is a nonzero matrix Y such that BYA is the 5 × 5 zero matrix.
Which one of the following holds ?
Questions Asked in CBSE CLASS XII exam
What is the Planning Process?
- CBSE CLASS XII - 2023
- Planning process steps
Evaluate \(\begin{vmatrix} cos\alpha cos\beta &cos\alpha sin\beta &-sin\alpha \\ -sin\beta&cos\beta &0 \\ sin\alpha cos\beta&sin\alpha\sin\beta &cos\alpha \end{vmatrix}\)
- CBSE CLASS XII - 2021
- Determinants
- Find the vector and the cartesian equations of the lines that pass through the origin and(5,-2,3).
- CBSE CLASS XII - 2021
- Three Dimensional Geometry
- A solution of Ni(NO3)2 is electrolysed between platinum electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?
- CBSE CLASS XII
- Electrochemistry
- What forces conspire to keep the workers in the bangle industry of Firozabad in poverty?
- CBSE CLASS XII
- Lost Spring
Concepts Used:
Invertible matrices
A matrix for which matrix inversion operation exists, given that it satisfies the requisite conditions is known as an invertible matrix. Any given square matrix A of order n × n is called invertible if and only if there exists, another n × n square matrix B such that, AB = BA = In, where In is an identity matrix of order n × n.
For example,
It can be observed that the determinant of the following matrices is non-zero.