
Content Strategy Manager
Geometric series formula or the geometric sequence formula is used to calculate the sum of a finite geometric sequence. The term "sequence" refers to the order of things.. Number sequences follow certain principles and patterns. This pattern can be of any type and can be used from one phrase to the next. The geometric sequence is a sequence in which multiplication is required to get the next term. When each term in a series is multiplied by the previous term in the series, a geometric series is generated. The total of the sequence's terms can be calculated using plus or minus symbols. The geometric series will be generated as a result of this. The sequence will be in the following format: {a, ar, ar2, ar3, …….}. In this article, we will have a look at the geometric series formula and some related sample questions.
| Table of Contents |
Keyterms: Geometric series, Geometric progression, Multiplication, Minus, Symbols, Plus, Sequence, Ratio, Number
Geometric Series
[Click Here for Sample Questions]
The geometric progression is another name for a geometric series. It's a series in which the first term is multiplied by a fixed value to get the second term. This technique is repeated until the series reaches the appropriate or required number of terms. A geometric progression is one in which the progression increases in a defined way.
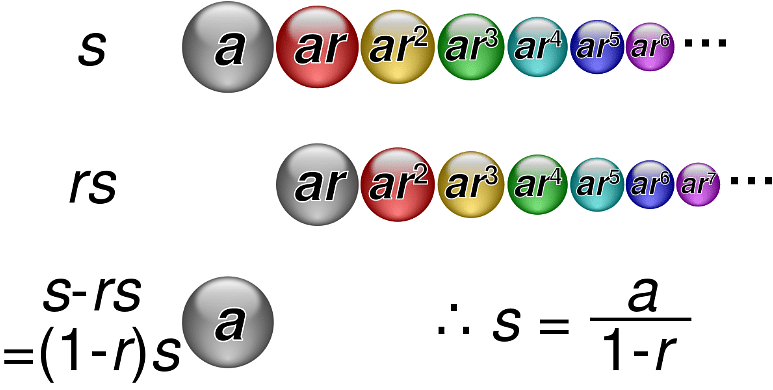
Geometric Series
The geometric series formula will be used to calculate the general term and the sum of all the terms in the series. As a result, the series follows a simple rule of multiplying a constant integer by one term to get to the next. As a result, any number of terms in such a series can be generated. We can look at such a series to learn about the fixed numbers for multiplication, often known as common ratios, denoted by the letter ‘r’.
Read More:
Geometric Series Formula
[Click Here for Sample Questions]
The formula for the sum of a geometric series is as follows:
Sn = \(\frac{a(r^n-1)}{r - 1} \)
- The nth term of a geometric sequence can be found using this formula.
- The sum of a finite geometric series is found.
- The sum of an infinite geometric series is found.
The formulas for finding the nth term, the sum of n terms, and the sum of infinite terms are among the formulas for a geometric series. Consider a geometric series with a first term and r as the common ratio.
The sequence will be in the following format: {a + ar + ar2 + ar3 +…….arn}
Formula 1- To find the nth term of a geometric sequence.
nth term = a rn-1
where a = first term
r = common ratio for all terms
n = no. of terms

Geometric Series and Common Ratio
Formula 2- To find the finite geometric series
The sequence will be in the following format: {a + ar + ar2 + ar3 + ... + a rn-1}
Sum of n terms = \(\frac{a(1 – r^n)}{1 – r}\)
where, a = first term
r = common ratio for all the terms
n = no. of terms
Formula 3- To find the sum of an infinite geometric series
The sequence will be in the following format: {a + ar + ar2 + ar3 +…… }
Sum of infinite geometric series =\(\frac{a}{1 - r} \)
where a = first term
r = common ratio for all terms
Geometric Series Applications
[Click Here for Sample Questions]
The geometric series is a mathematical miracle that governs much of the world. Geometric series played a pivotal role in the early development of calculus, are widely used in mathematics, and have applications in physics, engineering, biology, economics, computer science, queueing theory, and finance, among other fields.

Arithmetic Sequence vs Geometric Sequence
Things to Remember
- A numerical sequence is called a geometric sequence if the quotient of successive terms is a constant known as the common ratio.
- When each term in a series is multiplied by the previous term in the series, a geometric series is generated. The sequence will be of the following format: {a, ar, ar2, ar3, …….}
- The general term and the sum of all the terms in the series will be calculated using the geometric series formula.
- The formula for the geometric series is used to find the nth term of a geometric sequence, the sum of a finite geometric series, and the sum of an infinite geometric series.
- Geometric series are used in physics, engineering, biology, economics, computer science, queueing theory, and finance.
Sample Questions
Ques. Find the sum of the given infinite geometric series 8 + 12 + 18 + 27….if it exists. (3 marks)
Ans. First, we have to find the common ratio r.
So the formula for r will be = a2/a1
r = 12/8
= 3/2
As, r = 3/2 is not less than 1, hence the given series has got no sum.
Ques. Find out S10 if the given series is 2, 40, 800,….. (3 marks)
Ans. From the series given, we find that a = 2, common ratio r = 20 and n = 10
In the series, the 10th term is figured out by-
S10 = a(1 – rn)/1 – r
= 2(1 - 2010)/1 - 20
= 2(-1.024 1013)/ -19
= 1.0778 x 1012
Ques. Find out the sum of a given geometric sequence if a = 5, common ratio r = 1.5 and n = 10. (3 marks)
Ans. In order to solve the sum of given geometric series
Given details are as follows: a = 5, r = 1.5 and n = 10
Sn = a(1 - rn)/1 -r, hence
The sum of ten terms will be as
S10 =5(1 – 1.510)/1 – 1.5
S10 = 566.65
Ques. Solve out the sum of given geometric series if a = 3, r = 0.5 and n = 5. (3 marks)
Ans. Given quantities are: a = 3, r = 0.5, n = 5
S5 = a(1 – rn)/1 – r
= 3(1 – 0.55)/1 – 0.5
= 5.812
Hence the sum of the given geometric series will be 5.812.
Ques. Add the following infinite sum 27 + 18 + 12 + … (3 marks)
Ans. It is a geometric series. So by applying the formula for geometric series-
a1 = 27,
so r = a2 /a1 = 18 / 27 = 2 / 3
So, the sum of the infinity terms will be = a/(1 - r)
= 27/(1 - (2/3))
= 81
Ques. Find out the sum of the following series by applying the geometric series formula: (5 marks)
a) 1 + (1/3) + (1/9) + ... + (1/2187)
b) 1 + (1/3) + (1/9) + ...
Ans. In order to find out the sum of the already given two geometric series, we find that in both of the series given, the first term a = 1.
So, the common ratio, r will be = 1 / 3.
a) In the series given, nth term = 1/2187
So, a rn-1 = 1/37
⇒ 1 × (1/3)n-1 = 3-7
⇒ 3-n+1 = 3-7
⇒ - n + 1 = - 7
⇒ n = 8
Here we have to find out the sum of the first eight terms of the series given.
So, by applying the formula for the sum of the finite geometric series will be:
Sum of n terms = a(1 – rn)/1 – r
Hence the sum of eight terms will be = 1(1 – (1/3)8)/1 – 1/3
= 1(1 - 1/6561)2/3
= (6560/6561) × (3 / 2)
= 3280/2187
b) The series given is an infinite geometric series. So by applying the formula for the sum of the infinite geometric series that is the sum of infinite geometric series will be = a/(1 - r)
Hence the sum of the infinite geometric series given will be = 1/(1 - (1/3))
= 1/(2/3)
= 3/2
Ques. Solve the series and find out the 10th term of the geometric series 1, 4, 16, 64, …(5 marks)
Ans. In order to figure out the 10th term of the geometric series given.
The series is given and the first term, a will be = 1.
Hence the common ratio, r will be = 4 / 1 (or) 16 / 4 (else) 64 / 16 = 4.
So by applying the formulas of the geometric sequence, the nth term is solved out by using: nth term = arn-1
Substituting n = 10, a = 1, and r = 4 in the above mentioned formula: 10th term will be:
= 1 × 410-1
= 49
= 262,144
Read More:





Comments