
Content Writer
Geometric Mean is a measure of central tendency that evaluates the average of a series by finding the product of their values. It is the average or mean value that determines the power average of a growth series data.
- Measures of central tendency provide a summary of the whole data set values in Statistics.
- Mean, Median and Mode are the three most important measures of central tendencies.
- Mean of the data set is the average of the given set of numbers.
- Geometric Mean is one of the three types of mean along with Arithmetic Mean (AM), and Harmonic Mean (HM).
- It is used in the stock market to find the stock indexes and the annual return in the portfolio of securities.
Read More: NCERT Solutions for Class 11 Maths Sequences and Series
Key Terms: Geometric Mean, Mean, Measure of Central Tendency, Root, Discrete Data, Grouped Data, Geometric Mean Formula, Arithmetic Mean
What is Geometric Mean?
[Click Here for Sample Questions]
Geometric Mean (GM) is the average value or mean which indicates the central tendency of the set of numbers by finding out the product of their values.
- It is defined as the nth root of the product of n numbers.
- It involves multiplying the numbers and taking the nth root of the multiplied numbers, where n denotes the number of data values.
- For instance, the geometric mean of two numbers 3 and 1, is equal to √(3×1) = √3 = 1.732.
- Geometric mean and arithmetic mean are two different types of mean in Mathematics and Statistics.
- In arithmetic mean, the data values are added and then divided by the total number of values.
- In geometric mean, the data values are multiplied, and then the root is taken with the radical index for the total number of data values.
- If there are two data values, we take the square root, or if we have three data, then we take the cube root, and so on.
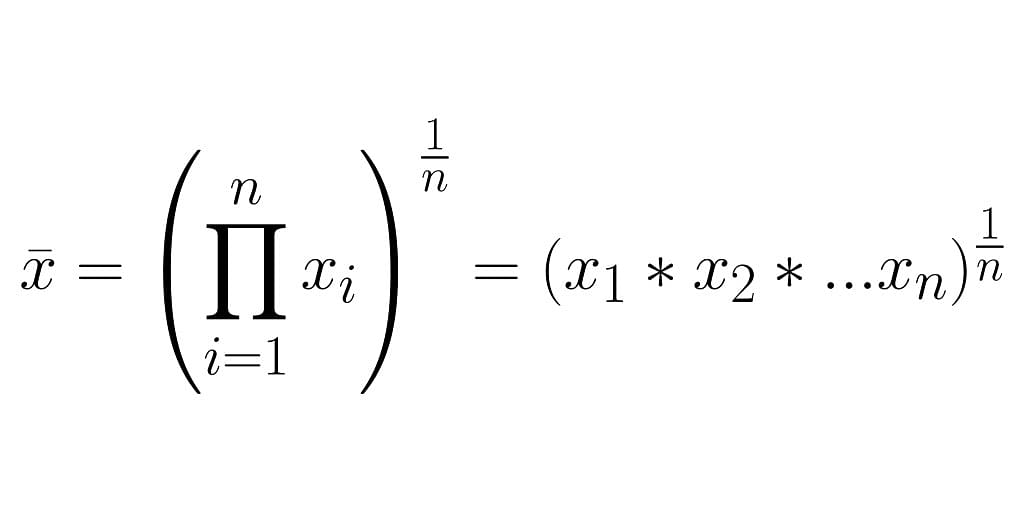
Geometric Mean Formula
Read More:
Geometric Mean Formula
[Click Here for Previous Years Questions]
Geometric Mean (G.M) of a series containing n numbers or observations is the nth root of the product of their values.
If x1, x2 …. Xn are the data values or observations, then the geometric mean is given as
\(\begin{array}{l}G. M = \sqrt[n]{x_{1}\times x_{2}\times …x_{n}}\end{array}\)
Geometric Mean Formula can also be written as
\(\begin{array}{l}G. M = (x_{1}\times x_{2}\times …x_{n})^{^{\frac{1}{n}}}\end{array}\)
On taking logarithms on both sides, we get
log GM = log (x₁ · x₂ · ... · xₙ)1/n
= (1/n) log (x₁ · x₂ · ... · xₙ)
= (1/n) [log x₁ +log x₂ + ... + log xₙ]
= (∑ log xᵢ) / n
Therefore, Geometric Mean Formula will be
\(\begin{array}{l}G.M = Antilog\frac{\sum \log x_{i}}{n}\end{array}\)
Where n = f1 + f2 +…...+ fn.
It is also represented as:
\(\begin{array}{l}G.M. =\sqrt[n]{\prod_{i=1}^{n}x_{i}}\end{array}\)
For any Grouped Data, Geometric Mean can be calculated as
\(\begin{array}{l}GM = Antilog\frac{\sum f \log x_{i}}{n}\end{array}\)
Geometric Mean Examples
[Click Here for Sample Questions]
Here are some solved examples on Geometric Mean for better concept clarity:
Example 1: Calculate the geometric mean of the given data set: 2, 4, 6, 8, 10, 12.
Solution: The given data set is 2, 4, 6, 8, 10, and 12.
- Product of Terms = 2 × 4 × 6 × 8 × 10 × 12 = 46080
- Number of Terms (n) = 6
Using the Geometric Mean Formula
\(\begin{array}{l}G. M = (x_{1}\times x_{2}\times …x_{n})^{^{\frac{1}{n}}}\end{array}\)
GM = (2 × 4 × 6 × 8 × 10 × 12)1/n
GM = (46080)1/6
GM = 5.98
Thus, the geometric mean of the given data set is 5.98.
Example 2: What will be the geometric mean of the given data?
| x | Log x |
|---|---|
| 45 | 1.653 |
| 60 | 1.778 |
| 48 | 1.681 |
| 100 | 2.000 |
| 65 | 1.813 |
| Total | 8.925 |
Solution: The total number of observations in the given data set is 5. Thus, n = 5.
Using the Geometric Mean Formula,
\(\begin{array}{l}G.M = Antilog\frac{\sum \log x_{i}}{n}\end{array}\)
G.M. = Antilog 8.925/5
G.M. = Antilog 1.785 = 60.95
Thus, the geometric mean of the given data set is 60.95.
Read More: Important Questions for Class 11 Maths Sequences and Series
Difference Between Arithmetic Mean and Geometric Mean
[Click Here for Previous Years Questions]
Geometric Mean and Arithmetic Mean are the two major types of mean in Statistics.
Arithmetic Mean
Arithmetic mean is calculated by dividing the sum of the observations by the total number of observations.
Example: Consider a data set 5, 10, 15, and 20.
Arithmetic Mean = Sum of Observations/Number of Observations
- Arithmetic Mean = (5+10+15+20)/4
- Arithmetic Mean = 50/4 = 12.5
Geometric Mean
Geometric Mean is calculated by multiplying all the data or numbers in the given observation set and taking the nth root for the obtained result.
Example: Consider a data set 4, 10, 16, and 24.
Here, Number of Observations (n) = 4
Geometric Mean = 4th root of (4 ×10 ×16 × 24)
- Geometric Mean = 153601/4
- Geometric Mean = 11.13
Relation Between AM, GM and HM
[Click Here for Sample Questions]
The relation between the Arithmetic Mean, Geometric Mean, and Harmonic Mean can be given by finding out the formulas of all three types of the mean.
Suppose that “x” and “y” are the two data values or numbers. Thus, n = 2.
Arithmetic Mean (AM) = (a+b)/2
⇒ 1/AM = 2/(a+b) ……. (1)
Geometric Mean (GM) = √(ab)
⇒ GM2 = ab ……. (2)
Harmonic Mean (HM)= 2/[(1/a) + (1/b)]
⇒ HM = 2/[(a+b)/ab
⇒ HM = 2ab/(a+b) …. (3)
Substituting (1) and (2) in (3), we get
HM = GM2/AM
⇒ GM2 = AM × HM
Thus,
| GM = √[ AM × HM] |
Hence, the relation between AM, GM, and HM is GM2 = AM × HM.
Geometric Mean Properties
[Click Here for Previous Years Questions]
The important properties of Geometric Mean are listed below:
- The geometric mean of a data set is always less than the arithmetic mean of a data set.
- The product of the values remains the same if each value in the data set is substituted by the G.M.
- The ratio of the corresponding values of the geometric mean in two series is equal to the ratio of their geometric means.
- The product of the corresponding values of the geometric mean in two series is equal to the product of their geometric mean.
Check More:
Applications of Geometric Mean
[Click Here for Sample Questions]
Geometric Mean is assumed to describe the data that can be interpreted as a scaling factor. Geometric mean is applied to positive values and is often used for the set of numbers whose values are exponential and are meant to be multiplied together. It means that there will be no null/zero value and negative value.
Some important applications of Geometric Mean are as follows:
- Geometric Mean is used in stock indexes.
- Most of the value line indexes used by financial departments use geometric mean.
- Geometric mean is used to calculate the annual return on the portfolio.
- It is used to find the average growth rates or the compounded annual growth rate.
- Geometric Mean is used in cell division and bacterial growth studies, etc.
Advantages of Geometric Mean
[Click Here for Previous Years Questions]
The advantages of Geometric Mean are listed as follows:
- Geometric Mean can be found in all the observations.
- It is less disturbed by tough values.
- It can be easily defined.
- It gives more meaning to small items.
- It is effective on many algebraic equations.
- It is suitable for all the percentages, averages, ratios, and rates.
- The difference in the observations does not affect the geometric mean.
Read More: Data Collection and Organization
Limitations of Geometric Mean
[Click Here for Sample Questions]
Geometric Mean has some limitations which are listed as follows:
- It is slightly difficult to understand in comparison to Arithmetic Mean.
- The geometric mean may or may not be the actual value of the series.
- The geometric mean cannot be calculated if any of the items in the series is negative or zero.
- It shows the property of the ratio of the change and not the actual difference of the change as the case in arithmetic means.
Things to Remember
- Geometric Mean is the average in which the numbers of a data set are multiplied and then their nth root is computed.
- It is the nth root of the product of n values, where n is the number of values.
- It involves roots and multiplication instead of addition and division.
- Geometric Mean Formula is given as \(\begin{array}{l}G. M = \sqrt[n]{x_{1}\times x_{2}\times …x_{n}}\end{array}\).
- It is also calculated using the formula \(\begin{array}{l}G.M = Antilog\frac{\sum \log x_{i}}{n}\end{array}\).
- Geometric Mean for a data set is always less than the arithmetic mean for the data set.
- The logarithm of the geometric mean is the arithmetic mean of the logarithms of given values.
- Geometric mean is used to calculate average growth rates and stock indexes.
Previous Year Questions
- If g1, g2 are two geometric means and a1is the arithmetic mean…
- For a sequence, {an}, a1 = 2 and…
- If the first and the (2n - 1)th term of an AP, GP, and HP… (JEE Advanced - 1988)
- Let a1, a2, a3, ...........be the sequence, then the sum expressed…
- If the sum of the first ten terms of the series… (JEE Main - 2016)
- The coefficient of x3 in the infinite series expansion of… (WBJEE - 2014)
- If m is a root of the equation (1 - ab)...
- In a G.P. of an even number of terms, the sum of all terms…
- In a geometric progression consisting of positive terms, each term… (AIEEE - 2007)
- The sum of the first 10 terms of a G.P. is equal to 244 times…
Sample Questions
Ques. Find the Geometric Mean of the given data values 10, 25, 5, and 30. (3 Marks)
Ans. Given data values are 10, 25, 5, and 30.
Using the Geometric Mean Formula,
\(\begin{array}{l}G. M = \sqrt[n]{x_{1}\times x_{2}\times …x_{n}}\end{array}\)
GM = 4√10 × 25 × 5 × 30
GM = 4√37500
GM = 13.915
Thus, the geometric mean of the given data values is 13.915.
Ques. Determine the geometric mean of the following grouped data for the frequency distribution of weights. (5 Marks)

Ans. From the given data, n = 160.
| Weights of the ear heads (g) | No of the ear heads (f) | Mid x | Log x | f log x |
|---|---|---|---|---|
| 60-80 | 22 | 70 | 1.845 | 40.59 |
| 80-100 | 38 | 90 | 1.954 | 74.25 |
| 100-120 | 45 | 110 | 2.041 | 91.85 |
| 120-140 | 35 | 130 | 2.114 | 73.99 |
| 140-160 | 20 | 150 | 2.176 | 43.52 |
| Total | 160 | 324.2 |
Using the Geometric Mean Formula for Grouped Data,
\(\begin{array}{l}G.M. = Antilog\frac{\sum f \log x_{i}}{n}\end{array}\)
G.M. = Antilog (324.2 /160)
G.M. = Antilog (2.02625)
G.M. = 106.23
Thus, the geometric mean of the given data set is 106.23.
Ques. What will be the geometric mean of the sequence, 5, 10, 15, and 20? (3 Marks)
Ans. The sequence is given as 5, 10, 15, and 20.
Product of Terms = 5 × 10 × 15 × 20 = 15000
Number of Terms (n) = 4
Using the Geometric Mean Formula
\(\begin{array}{l}G. M = \sqrt[n]{x_{1}\times x_{2}\times …x_{n}}\end{array}\)
GM = 4√(5 × 10 × 15 × 20)
GM = 4√(15000)
GM = 11.06
Thus, the geometric mean of the given sequence is 1.06.
Ques. If AM and HM of the data sets are 4 and 25 respectively, then find the GM. (3 Marks)
Ans. Given that,
- Arithmetic Mean (AM) = 4
- Harmionic Mean (HM) = 25
We know that the relation between AM, GM, and HM is given as
GM = √ [ AM × HM]
Substitute the values in the above equation,
GM = √[4 × 25]
GM = √100 = 10
Hence, the geometric mean is 10.
Ques. Calculate the geometric mean of 2 and 8. (3 Marks)
Ans. Let us assume that
- a = 2
- b = 8
Here, the number of the data or terms, n = 2
If n = 2, then the formula for the geometric mean is √(ab).
Therefore, GM = √(2×8)
GM = √16 = 4
So, the geometric mean of 2 and 8 is 4.
Ques. What will be the geometric mean of the annual percentage growth rate of profits in business corporate as given below: (3 Marks)

Ans. The total number of observations is five, thus, n = 5.
Using the Geometric Mean Formula,
\(\begin{array}{l}G.M = Antilog\frac{\sum \log x_{i}}{n}\end{array}\)
G.M. = Antilog 9.1710/5
G.M. = Antilog 1.8342
G.M. = 68.26
Thus, the geometric mean for the annual percentage growth rate of profits is 68.26.
Ques. The population in the city increased at the rate of 15% and 25% for two successive years. In the next year, it decreased at the rate of 5%. Find the average rate of growth. (3 Marks)
Ans. Suppose that the population is 100.
| Percentage Rise in Population | Population at the End of the year | log xi |
|---|---|---|
| 15 | 115 | 2.0607 |
| 25 | 125 | 2.0969 |
| 5 | 95 | 1.9777 |
| Total | 6.1353 | |
Using the Geometric Mean Formula,
\(\begin{array}{l}G.M = Antilog\frac{\sum \log x_{i}}{n}\end{array}\)
G.M. = Antilog 6.1353/3
G.M. = Antilog 2.0451
G.M. = 110.9
Thus, the average growth rate is 110.9.
Ques. Calculate the geometric mean of the given sequence: 4, 8, 12, 16, 20. (3 Marks)
Ans. The given sequence is 4, 8, 12, 16, and 20.
- Product of Terms= 4 × 8 × 12 × 16 × 20 = 122880
- Number of Terms (n) = 5
Using the Geometric Mean Formula
\(\begin{array}{l}G. M = \sqrt[n]{x_{1}\times x_{2}\times …x_{n}}\end{array}\)
GM = 5√(4 × 8 × 12 × 16 × 20)
GM = 5√(122880)
GM = 10.42
Thus, the geometric mean of the given data set is 10.42.
Ques. What will be the number of terms in a sequence if the geometric mean is 16 and the product of terms is 16777216? (3 Marks)
Ans. Given that,
Product of Terms (P) = 16777216
Geometric Mean (GM) = 16
Using the Geometric Mean Formula
\(\begin{array}{l}G. M = (x_{1}\times x_{2}\times …x_{n})^{^{\frac{1}{n}}}\end{array}\)
1/n = log GM/log P
n = log P/log GM
n = log 16777216/log 16
n = 24/4 = 6
Thus, the number of terms in the sequence is 6.
Ques. Determine the number of terms if the geometric mean of a sequence is 32 and the product of terms is 1024. (3 Marks)
Ans. Given that,
- Product of Terms (P) = 1024
- Geometric Mean (GM) = 32
Using the Geometric Mean Formula
\(\begin{array}{l}G. M = (x_{1}\times x_{2}\times …x_{n})^{^{\frac{1}{n}}}\end{array}\)
1/n = log GM/log P
n = log P/log GM
n = log 1024/log 32
n = 10/5 = 2
Therefore, the number of terms are 2.
Check-Out:





Comments