MHT CET 2024 question paper is available here. MHT CET 2024 question paper comprises 150 MCQs carrying a total weightage of 200 marks. MHT CET 2024 Question Paper for PCM is divided into three subjects- Physics, Chemistry and Mathematics. The Physics and Chemistry section of MHT CET 2024 question paper will include 50 questions (10 questions from Class 11 and 40 questions from Class 12th syllabus). Meanwhile, the Mathematics paper of MHT CET 2024 question paper will include 100 questions (20 questions from Class 11th and 80 questions from Class 12th syllabus).
MHT CET 2024 PCM Question Paper PDF Download
| MHT CET 2024 PCM Question Paper With Answer Key | Check Solutions |
MHT CET 2024 PCM Solution
Question 1:
Force between two point charges q₁ and q₂ placed in vacuum at a distance r cm apart is F. Force between them when placed in a medium having dielectric K = 5 at r/5 cm apart will be:
View Solution
The electrostatic force between two point charges in vacuum is:
F = (1 / 4πε₀) × (q₁q₂ / r²).
In a medium with dielectric constant K, the force becomes:
F' = (1 / 4πKε₀) × (q₁q₂ / r'²).
If K = 5 and r' = r / 5, substitute these values:
F' = (1 / 4π(5)ε₀) × (q₁q₂ / (r / 5)²).
Simplify:
F' = (25 / 5) × (1 / 4πε₀) × (q₁q₂ / r²) = 5F.
Thus, the new force is 5F.
Question 2:
A thin circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its center and perpendicular to its plane with angular velocity ω. If another disc of the same dimensions but of mass M / 2 is placed gently on the first disc coaxially, then the new angular velocity of the system is:
View Solution
Using conservation of angular momentum:
I₁ω₁ = I₂ω₂.
Initial moment of inertia: I₁ = (1/2)MR².
Final moment of inertia after adding the second disc:
I₂ = (1/2)MR² + (1/2)(M/2)R² = (3/4)MR².
Substituting into the conservation equation:
(1/2)MR²ω = (3/4)MR²ω₂.
Solve for ω₂:
ω₂ = (1/2) / (3/4) ω = (2/3)ω.
Thus, the new angular velocity is (2/3)ω.
Question 3:
Correct Bernoulli’s equation is (symbols have their usual meaning):
View Solution
Bernoulli’s theorem states that for an incompressible, non-viscous fluid in steady flow, the sum of pressure energy, potential energy, and kinetic energy per unit volume is constant:
P + ρgh + (1/2)ρv² = constant.
Here:
- P is the pressure.
- ρ is the density of the fluid.
- g is the acceleration due to gravity.
- h is the height above a reference point.
- v is the velocity of the fluid.
Other options incorrectly use mass instead of density or modify the energy terms improperly.
Question 4:
Two projectiles are projected at 30° and 60° with the horizontal with the same speed. The ratio of the maximum height attained by the two projectiles respectively is:
View Solution
The maximum height attained by a projectile is given by:
H = (u² × sin²θ) / (2g),
where:
- u is the initial velocity,
- θ is the angle of projection,
- g is the acceleration due to gravity.
Let the two projectiles have angles of projection θ₁ = 30° and θ₂ = 60°.
For the first projectile: H₁ = (u² × sin²30°) / (2g).
For the second projectile: H₂ = (u² × sin²60°) / (2g).
The ratio of their maximum heights is:
H₁ / H₂ = (sin²30°) / (sin²60°).
Substitute sin30° = 1/2 and sin60° = √3/2:
H₁ / H₂ = ((1/2)²) / ((√3/2)²) = (1/4) / (3/4) = 1 / 3.
Thus, the ratio of the maximum heights is 1 : 3.
Question 5:
A real gas within a closed chamber at 27°C undergoes the cyclic process as shown in the figure. The gas obeys the equation PV³ = RT for the path A to B. The net work done in the complete cycle is (assuming R = 8 J/mol·K):
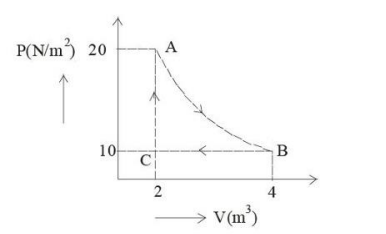
View Solution
The cyclic process consists of three steps: AC (isochoric), BC (isobaric), and AB (PV³ = RT).
Step 1: Isochoric process (AC)
Work done (W) = 0 (no change in volume).
Step 2: Isobaric process (BC)
Work done: W = P × ΔV.
W = 10 × (2 - 4) = -20 J.
Step 3: Path AB (PV³ = RT)
Work done: W = ∫ P dV = ∫ (RT / V³) dV.
W = -RT / 2 [(1/V²)] from V₁ to V₂.
Substitute V₁ = 2, V₂ = 4, R = 8 J/mol·K, and T = 300 K:
W = (8 × 300) / 2 × (1/16 - 1/4) = 225 J.
Total Work Done:
W = W(AC) + W(BC) + W(AB) = 0 - 20 + 225 = 205 J.
Question 7:
A monkey of mass 50 kg climbs on a rope that can withstand a tension of 350 N. If the monkey initially climbs down with an acceleration of 4 m/s² and then climbs up with an acceleration of 5 m/s², choose the correct option (g = 10 m/s²):
View Solution
Step 1: Climbing upward
The tension in the rope while climbing upward is given by: T = m(g + a), where:
m = 50 kg (mass of the monkey),
g = 10 m/s² (gravitational acceleration),
a = 5 m/s² (acceleration while climbing upward).
Substitute values:
T = 50 × (10 + 5) = 750 N.
Since T > 350 N, the rope will break while climbing upward.
Step 2: Climbing downward
The tension in the rope while climbing downward is given by: T = m(g - a).
Substitute values (a = 4 m/s²):
T = 50 × (10 - 4) = 300 N.
Since T < 350 N, the rope will not break while climbing downward.
Question 8:
Figure shows a part of an electric circuit. The potentials at points a, b, and c are 30 V, 12 V, and 2 V, respectively. The current through the 20 Ω resistor will be:
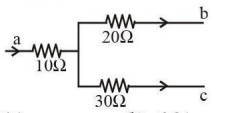
View Solution
Step 1: Apply Ohm's Law
The voltage difference across the 20 Ω resistor is given by V = V_b - V_c.
Substitute the values:
V = 12 V - 2 V = 10 V.
Using Ohm's Law (V = IR), the current is:
I = V / R = 10 / 20 = 0.4 A.
Step 2: Verify using Kirchhoff's Laws
Calculate the currents through other resistors using Ohm's Law:
Current through the 10 Ω resistor (I₁):
I₁ = (V_a - V_b) / 10 = (30 - 12) / 10 = 1.8 A.
Current through the 30 Ω resistor (I₃):
I₃ = (V_b - V_c) / 30 = (12 - 2) / 30 = 0.333 A.
At the junction, I₁ = I₂ + I₃, which verifies I₂ = 0.4 A.
Question 9:
A current of 200 μA deflects the coil of a moving coil galvanometer through 60°. The current to cause deflection through π/10 radians is:
View Solution
The deflection in a moving coil galvanometer is directly proportional to the current:
I ∝ θ.
Let:
I₁ = 200 μA, θ₁ = 60°, and θ₂ = π/10 radians.
Convert 60° to radians:
θ₁ = 60° = π/3 radians.
Using the proportionality relation:
I₂ / I₁ = θ₂ / θ₁.
Substitute the values:
I₂ / 200 = (π/10) / (π/3).
Simplify:
I₂ / 200 = 3 / 10.
Solve for I₂:
I₂ = 200 × (3 / 10) = 60 μA.
Question 10:
The value of acceleration due to gravity at Earth's surface is 9.8 m/s². The altitude above its surface at which the acceleration due to gravity decreases to 4.9 m/s² is close to: (Radius of Earth R = 6.4 × 10⁶ m)
View Solution
The acceleration due to gravity at an altitude h is given by:
gₕ = g / (1 + h / R)².
Given:
gₕ = g / 2.
Substitute into the formula:
g / 2 = g / (1 + h / R)².
Simplify:
(1 + h / R)² = 2.
Take the square root:
1 + h / R = √2.
Solve for h:
h / R = √2 - 1.
Substitute R = 6.4 × 10⁶ m:
h = (√2 - 1) × 6.4 × 10⁶.
Simplify:
h = (1.414 - 1) × 6.4 × 10⁶ = 0.414 × 6.4 × 10⁶ = 2.6 × 10⁶ m.
Question 11:
Relative permittivity and permeability of a material are εᵣ and μᵣ, respectively. Which of the following values of these quantities are allowed for a diamagnetic material?
View Solution
For a diamagnetic material:
The relative permeability μᵣ is slightly less than 1, as diamagnetic materials repel magnetic fields.
The relative permittivity εᵣ is always greater than 1, as it represents the material's ability to polarize in response to an electric field.
Among the given options, εᵣ = 1.5 and μᵣ = 0.5 satisfies these conditions.
Question 12:
The magnetic flux through a coil perpendicular to its plane is varying according to the relation φ = 5t3 + 4t2 + 2t - 5. If the resistance of the coil is 5 Ω, then the induced current through the coil at t = 2 seconds will be:
View Solution
Solution:
The induced EMF (e) is given by Faraday’s Law:
e = |dφ/dt|
Given:
φ = 5t³ + 4t² + 2t - 5
Differentiate φ with respect to t:
e = |15t² + 8t + 2|
At t = 2 seconds:
e = 15(2)² + 8(2) + 2 = 60 + 16 + 2 = 78 V
The induced current (i) is given by Ohm’s Law:
i = e / R
Substitute R = 5 Ω:
i = 78 / 5 = 15.6 A
Question 13:
A solid metallic cube having a total surface area of 24 m2 is uniformly heated. If its temperature is increased by 10°C, calculate the increase in the volume of the cube. (Given: α = 5.0 × 10⁻⁴ °C⁻¹)
View Solution
Solution:
The increase in volume is given by:
ΔV = V0 γ ΔT,
where:
- V0 = a³ (initial volume of the cube),
- γ = 3α (coefficient of volumetric expansion),
- ΔT = 10°C (temperature change).
The surface area of a cube is:
Total Surface Area = 6a²
Given 6a² = 24 m², solve for a:
a² = 24 / 6 = 4 m² → a = 2 m
The initial volume is:
V0 = a³ = 2³ = 8 m³ = 8 × 10⁶ cm³
Substitute into the formula for ΔV:
ΔV = 8 × 10⁶ × (3 × 5 × 10⁻⁴) × 10
ΔV = 8 × 10⁶ × 15 × 10⁻³ = 1.2 × 10⁵ cm³
Question 14:
Two coils are placed close to each other. The mutual inductance of the pair of coils depends upon:
View Solution
Solution:
The mutual inductance between two coils is defined as:
M = Φ / I,
where Φ is the magnetic flux in one coil due to the current I in the other coil.
The mutual inductance depends on:
- The relative position and orientation of the two coils (determines the coupling of magnetic fields).
- The number of turns and dimensions of the coils.
- The magnetic permeability of the medium between the coils.
It does not depend directly on the current or the material of the coil wires.
Question 15:
A proton, an electron, and an alpha particle have the same energies. Their de-Broglie wavelengths will be compared as:
View Solution
Solution:
The de-Broglie wavelength is given by:
λ = h / √(2mE),
where h is Planck's constant, m is the mass of the particle, and E is its energy.
For particles with the same energy, λ ∝ 1 / √m.
The masses of the particles are:
- Electron (me): least mass,
- Proton (mp): greater mass,
- Alpha particle (mα = 4mp): greatest mass.
Since λ ∝ 1 / √m, the order of wavelengths is:
λe > λp > λα.
Question 16:
An ice cube has a bubble inside. When viewed from one side, the apparent distance of the bubble is 12 cm. When viewed from the opposite side, the apparent distance of the bubble is 4 cm. If the side of the ice cube is 24 cm, the refractive index of the ice cube is:
View Solution
Solution:
The refractive index (μ) is given by:
μ = Real Depth / Apparent Depth.
Let the real depth of the bubble be x cm. When viewed from one side, the apparent depth is 12 cm, and when viewed from the opposite side, the apparent depth is 24 - x cm.
From the refractive index formula:
μ = x / 12 (from one side),
μ = (24 - x) / 4 (from the opposite side).
Equate the two expressions for μ:
x / 12 = (24 - x) / 4.
Simplify:
4x = 12(24 - x).
4x = 288 - 12x.
16x = 288 → x = 18 cm.
Substitute x = 18 cm into μ = x / 12:
μ = 18 / 12 = 3/2.
Question 17:
The longest wavelength associated with the Paschen series is:
(Given RH = 1.097 × 107 SI unit)
View Solution
Solution:
The wavelength for the Paschen series is given by:
1/λ = RH (1/n12 - 1/n22),
where:
- n1 = 3 (Paschen series),
- n2 = 4 (for the longest wavelength, n2 is the next level above n1).
Substitute:
1/λ = RH (1/32 - 1/42).
Simplify:
1/λ = RH (1/9 - 1/16).
1/λ = RH (16 - 9) / 144.
1/λ = RH × 7/144.
Substitute RH = 1.097 × 107:
1/λ = 1.097 × 107 × 7/144.
1/λ = 7.679 × 107 / 144.
λ = 144 / 7.679 × 107 ≈ 1.876 × 10-6 m.
Question 18:
The ratio of the mass densities of nuclei of 40Ca and 16O is close to:
View Solution
Solution:
Nuclear density (ρ) is nearly constant for all nuclei, regardless of their atomic number or mass number. This is because both the mass and the volume of the nucleus are proportional to the mass number (A).
1. Density of 40Ca:
For 40Ca, mass number A = 40. The nuclear density remains constant:
ρCa = constant.
2. Density of 16O:
For 16O, mass number A = 16. The nuclear density is the same as for 40Ca:
ρO = constant.
3. Ratio of Densities:
Since nuclear density is constant:
ρCa / ρO = 1.
Question 19:
Point charge of 10 μC is placed at the origin. At what location on the X-axis should a point charge of 40 μC be placed so that the net electric field is zero at x = 2 cm on the X-axis?
View Solution
Solution:
To determine the location x0 where the second charge (40 μC) should be placed such that the net electric field is zero at x = 2 cm:
Step 1: Electric Field Balance
At x = 2 cm, the electric field contributions from the two charges must cancel each other:
Enet = 0 → k × (10 × 10-6) / (22) = k × (40 × 10-6) / (x0 - 2)2.
Step 2: Simplify the Relation
Cancel k and simplify:
(10 / 4) = (40 / (x0 - 2)2).
1 / 2 = 2 / (x0 - 2)2.
Step 3: Solve for x0
(x0 - 2)2 = 4.
x0 - 2 = ±2.
x0 = 4 cm or x0 = 6 cm.
Step 4: Select the Correct Value of x0
Since the second charge is placed to the right of x = 2 cm, the correct position is:
x0 = 6 cm.
Question 20:
A magnetic needle is kept in a non-uniform magnetic field. It experiences:
View Solution
Solution:
A magnetic needle kept in a non-uniform magnetic field experiences both a force and a torque due to unequal forces acting on its poles.
The non-uniform magnetic field exerts different magnitudes of forces on the north and south poles of the needle, resulting in a net force on the needle.
Additionally, these forces create a torque that tends to align the needle with the magnetic field lines.
Question 21:
A current-carrying rectangular loop PQRS is made of uniform wire. The length PR = QS = 5 cm and PQ = RS = 100 cm. If the ammeter current reading changes from I to 2I, the ratio of magnetic forces per unit length on the wire PQ due to wire RS in the two cases respectively FIPQ : F2IPQ is:
View Solution
Solution:
The magnetic force per unit length F/ℓ between two parallel current-carrying wires is given by:
F/ℓ = (μ0 I1 I2) / (4πr),
where:
- μ0 is the permeability of free space,
- I1 and I2 are the currents in the two wires,
- r is the distance between the wires.
Step 1: Proportionality for F/ℓ
The magnetic force is directly proportional to the product of the currents:
F1 ∝ I² (when the current is I).
When the current changes to 2I:
F2 ∝ (2I)² = 4I².
Step 2: Ratio of Forces
The ratio of the magnetic forces is:
F1 / F2 = I² / 4I² = 1:4.
Question 22:
At which temperature will the r.m.s. velocity of a hydrogen molecule be equal to that of an oxygen molecule at 47°C?
View Solution
Solution:
The r.m.s. velocity \( v_{\text{rms}} \) of a gas molecule is given by:
vrms = √(3RT / M),
where:
- R is the gas constant,
- T is the temperature (in Kelvin),
- M is the molar mass of the gas.
Step 1: Equating the r.m.s. velocities
For hydrogen (H2) and oxygen (O2):
vrms(H2) = vrms(O2).
√(3RTH2 / MH2) = √(3RTO2 / MO2).
Square both sides:
TH2 / MH2 = TO2 / MO2.
Rearrange for TH2:
TH2 = TO2 × (MH2 / MO2).
Step 2: Substitute values
For oxygen:
TO2 = 47°C + 273 = 320 K.
The molar masses are:
MH2 = 2, MO2 = 32.
Substitute into the equation:
TH2 = 320 × (2 / 32).
Simplify:
TH2 = 320 × 1 / 16 = 20 K.
Question 23:
A light-emitting diode (LED) is fabricated using GaAs semiconductor material whose band gap is 1.42 eV. The wavelength of light emitted from the LED is:
View Solution
Solution:
The wavelength of emitted light is related to the band gap energy Eg by the equation:
Eg (eV) = 1240 / λ (nm).
Rearrange to find the wavelength:
λ = 1240 / Eg.
Step 1: Substitute the given values
Given:
Eg = 1.42 eV.
Substitute:
λ = 1240 / 1.42.
λ ≈ 875 nm.
Question 24:
A steel wire with mass per unit length 7.0 × 10⁻³ kg/m is under a tension of 70 N. The speed of transverse waves in the wire will be:
View Solution
The speed of transverse waves in a wire is given by:
v = √(T / μ),
where:
- T is the tension in the wire,
- μ is the mass per unit length.
Step 1: Substitute the given values:
T = 70 N, μ = 7.0 × 10⁻³ kg/m.
Substitute into the formula:
v = √(70 / (7.0 × 10⁻³)).
Step 2: Simplify the calculation:
v = √(70 / 0.007) = √10000.
v = 100 m/s.
Question 25:
Two vessels A and B are of the same size and are at the same temperature. Vessel A contains 1 g of hydrogen and vessel B contains 1 g of oxygen. PA and PB are the pressures of the gases in A and B respectively. Then PA / PB is:
View Solution
Solution:
By the ideal gas equation:
P × V = n × R × T, which implies P ∝ n,
where n is the number of moles.
Step 1: Calculate the number of moles
For hydrogen (H2):
MH2 = 2 g/mol, nA = Mass / Molar Mass = 1 / 2 = 0.5 mol.
For oxygen (O2):
MO2 = 32 g/mol, nB = Mass / Molar Mass = 1 / 32 = 0.03125 mol.
Step 2: Ratio of pressures
PA / PB = nA / nB = 0.5 / 0.03125.
Simplify:
PA / PB = 16.
Question 26:
A wire of length 1 m moving with velocity 8 m/s at right angles to a magnetic field of 2 T. The magnitude of induced emf between the ends of the wire will be:
View Solution
Solution:
The induced emf ε in a moving conductor is given by:
ε = B × v × l,
where:
- B = 2 T is the magnetic field strength,
- v = 8 m/s is the velocity of the wire,
- l = 1 m is the length of the wire.
Step 1: Substitute the given values
Substitute B = 2 T, v = 8 m/s, and l = 1 m:
ε = 2 × 8 × 1.
Step 2: Simplify the calculation
ε = 16 V.
Question 27:
Two identical particles each of mass m go around a circle of radius a under the action of their mutual gravitational attraction. The angular speed of each particle will be:
View Solution
Solution:
The gravitational force provides the centripetal force for circular motion:
Fgravity = Fcentripetal.
The gravitational force between two particles is:
F = (G × M₁ × M₂) / d²,
where:
- G is the gravitational constant,
- M₁ = M₂ = m,
- d = 2a is the distance between the two particles.
Substitute:
F = (G × m²) / (2a)² = Gm² / 4a².
For circular motion:
F = m × ω² × r,
where r = a. Substitute F = Gm² / 4a²:
(Gm²) / (4a²) = m × ω² × a.
Simplify:
ω² = Gm / 4a³.
Take the square root:
ω = √(Gm / 4a³).
Question 28:
In an unbiased p-n junction, electrons diffuse from n-region to p-region because:
View Solution
In an unbiased p-n junction:
- The electron concentration in the n-region is much higher than in the p-region.
- Due to this concentration difference, electrons naturally diffuse from the n-region to the p-region (from high to low concentration).
- This diffusion creates a depletion region and establishes a built-in electric field that opposes further electron flow.
Question 29:
A particle is executing Simple Harmonic Motion (SHM). The ratio of potential energy and kinetic energy of the particle when its displacement is half of its amplitude will be:
View Solution
Solution:
The total energy in SHM is given by:
Etotal = (1/2) k A2,
where k is the spring constant and A is the amplitude of oscillation.
Step 1: Potential and Kinetic Energy
The potential energy at displacement x is:
PE = (1/2) k x2.
The kinetic energy is:
KE = Etotal - PE = (1/2) k A2 - (1/2) k x2.
Step 2: Displacement is half the amplitude
Substitute x = A/2:
PE = (1/2) k (A/2)2 = (1/2) k (A2 / 4) = (1/8) k A2.
KE = (1/2) k A2 - (1/8) k A2 = (4/8) k A2 - (1/8) k A2 = (3/8) k A2.
Step 3: Ratio of PE and KE
PE / KE = (1/8) k A2 / (3/8) k A2 = 1/3.
Question 30:
Eight equal drops of water are falling through air with a steady speed of 10 cm/s. If the drops coalesce, the new velocity is:
View Solution
Solution:
When the drops coalesce, the volume remains constant. Let:
r be the radius of each small drop, R be the radius of the combined drop.
Step 1: Volume conservation
The total volume of the eight small drops is:
8 × (4/3) π r3 = (4/3) π R3.
Simplify:
R3 = 8r3 → R = 2r.
Step 2: Relationship between terminal velocity and radius
The terminal velocity vT is proportional to the square of the radius:
vT ∝ r2.
Let v1 = 10 cm/s be the terminal velocity of the small drops, and v2 be the terminal velocity of the combined drop. Then:
v1 / v2 = (r / R)2.
Substitute R = 2r:
v1 / v2 = (r / 2r)2 = 1/4.
Step 3: Solve for v2
v2 = 4v1 = 4 × 10 = 40 cm/s.
Question 31:
In a coil, the current changes from -2 A to +2 A in 0.2 s and induces an emf of 0.1 V. The self-inductance of the coil is:
View Solution
Solution:
The emf induced in a coil is given by:
ε = L × (ΔI / Δt),
where:
- ε = 0.1 V is the induced emf,
- ΔI = Ifinal - Iinitial = 2 - (-2) = 4 A is the change in current,
- Δt = 0.2 s is the time interval,
- L is the self-inductance.
Step 1: Solve for L
L = ε × Δt / ΔI.
Substitute the values:
L = (0.1 × 0.2) / 4.
Simplify:
L = 0.02 / 4 = 0.005 H.
Convert to millihenries:
L = 5 mH.
Question 32:
For a uniform rectangular sheet shown in the figure, the ratio of moments of inertia about the axes perpendicular to the sheet and passing through O (the center of mass) and O' (corner point) is:
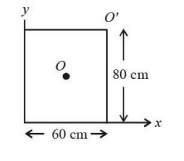
View Solution
Solution:
The moment of inertia (IO) of the rectangular sheet about an axis passing through O (center of mass) is given by:
IO = (M/12) × (a² + b²),
where a = 80 cm and b = 60 cm are the dimensions of the rectangle, and M is the mass of the sheet.
Substitute the values:
IO = (M/12) × (80² + 60²).
Calculate:
IO = (M/12) × (6400 + 3600) = (M/12) × 10000 = 10000M / 12.
Using the parallel axis theorem, the moment of inertia about O' is:
IO' = IO + M × d²,
where d is the perpendicular distance between O and O', given by:
d = √((a/2)² + (b/2)²) = √(40² + 30²) = 50 cm.
Substitute:
IO' = (10000M / 12) + M × 50².
Simplify:
IO' = (10000M / 12) + 2500M = (10000M / 12) + (30000M / 12) = 40000M / 12.
The ratio of moments of inertia is:
(IO / IO') = (10000M / 12) / (40000M / 12) = 10000 / 40000 = 1/4.
Question 33:
If n is the number density and d is the diameter of the molecule, then the average distance covered by a molecule between two successive collisions (i.e., mean free path) is represented by:
View Solution
Solution:
The mean free path (λ) is the average distance a molecule travels between two successive collisions. It is derived from the kinetic theory of gases and is given by the formula:
λ = 1 / √(2πnd²),
where:
- n is the number density of molecules (number of molecules per unit volume),
- d is the diameter of a molecule,
- π is the constant representing the geometric cross-sectional area of a circle.
Final Answer: λ = 1 / √(2πnd²).
Question 34:
A mixture of one mole of monoatomic gas and one mole of diatomic gas (rigid) are kept at room temperature (27°C). The ratio of specific heat of gases at constant volume respectively is:
View Solution
Solution:
For a monoatomic gas, the specific heat at constant volume (CV) is:
CV = (3/2)R.
For a diatomic gas (rigid), the specific heat at constant volume (C'V) is:
C'V = (5/2)R.
The ratio of specific heats is:
(CV / C'V) = ((3/2)R) / ((5/2)R) = 3/5.
Question 35:
In an a.c. circuit, voltage and current are given by:
V = 100 sin(100t) V and I = 100 sin(100t + π/3) mA. The average power dissipated in one cycle is:
View Solution
Solution:
The average power in one cycle is given by:
P_avg = V_rms × I_rms × cos(Δφ).
Here, V_rms = V_0 / √2 = 100 / √2, I_rms = I_0 / √2 = (100 × 10⁻³) / √2, and Δφ = π/3.
Substitute:
P_avg = (100 / √2) × (100 × 10⁻³ / √2) × cos(π/3).
Simplify:
P_avg = (100 × 0.1) / 2 × (1/2) = 2.5 W.
Question 36:
The difference between threshold wavelengths for two metal surfaces A and B having work functions:
ϕ_A = 9 eV and ϕ_B = 4.5 eV is:
(Given: h c = 1242 eV·nm)
View Solution
Solution:
The wavelength (λ) is related to the work function (ϕ) by:
λ = (hc) / ϕ.
For ϕ_A = 9 eV:
λ_A = 1242 / 9 = 138 nm.
For ϕ_B = 4.5 eV:
λ_B = 1242 / 4.5 = 276 nm.
The difference is:
Δλ = λ_B - λ_A = 276 - 138 = 138 nm.
Question 37:
The logic performed by the circuit shown in the figure is equivalent to:
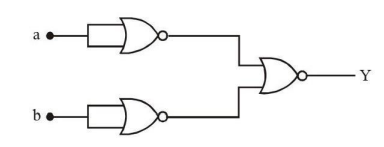
View Solution
Solution:
The circuit performs the following operations:
- The first two NOT gates take inputs a and b, and output their complements ¬a and ¬b.
- The OR gate combines these complements: ¬a + ¬b.
- The NOT gate takes the complement of the OR gate’s output: ¬(¬a + ¬b).
Using De Morgan’s law:
¬(¬a + ¬b) = a ∧ b (AND).
The circuit performs the logic of an AND gate.
Question 38:
A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance (2A/3) from the equilibrium position. The new amplitude of the motion is:
View Solution
Solution:
The velocity of a particle in SHM is:
v = ω√(A² - x²),
where A is the amplitude and x is the displacement.
Initially, at x = (2A/3), the velocity is:
v = ω√(A² - (2A/3)²).
Substitute:
v = ω√(A² - (4A²/9)) = ω√(5A²/9) = (ωA√5)/3.
When the speed is tripled, the velocity becomes:
3v = ω√(A'² - (2A/3)²),
where A' is the new amplitude.
Substitute for v:
3(ωA√5)/3 = ω√(A'² - (4A²/9)).
Simplify:
A√5 = √(A'² - (4A²/9)).
Square both sides:
5A² = A'² - (4A²/9).
Rearrange:
A'² = 5A² + (4A²/9) = (45A²/9) + (4A²/9) = (49A²/9).
Simplify:
A' = (7A/3).
Question 39:
The mass of proton, neutron, and helium nucleus are respectively 1.0073 u, 1.0087 u, 4.0015 u. The binding energy of the helium nucleus is:
View Solution
Solution:
The binding energy (BE) of a nucleus is calculated using:
BE = Δm × c²
Here, Δm is the mass defect. For helium nucleus:
Δm = (2 × mass of proton + 2 × mass of neutron) - mass of helium nucleus
Δm = (2 × 1.0073 + 2 × 1.0087) - 4.0015
Δm = 4.0310 - 4.0015 = 0.0295 u
Convert mass defect to energy using 1 u = 931.5 MeV/c²:
BE = 0.0295 × 931.5 = 28.4 MeV
Question 40:
A series LCR circuit is subjected to an AC signal of 200 V, 50 Hz. If the voltage across the inductor (L = 10 mH) is 31.4 V, then the current in this circuit is:
View Solution
Solution:
The voltage across the inductor is given by:
V_L = I × X_L
where X_L is the inductive reactance and is calculated as:
X_L = ωL
Step 1: Calculate angular frequency:
ω = 2πf = 2 × 3.14 × 50 = 314 rad/s
Step 2: Calculate X_L:
X_L = 314 × 10 × 10⁻³ = 3.14 Ω
Step 3: Calculate current:
I = V_L / X_L = 31.4 / 3.14 = 10 A
Question 41:
When two soap bubbles of radii a and b (b > a) coalesce, the radius of curvature of the common surface is:
View Solution
Solution:
The pressure inside a soap bubble is given by:
P = P₀ + 4T / R
For two bubbles with radii a and b:
P₁ = P₀ + 4T / a, and P₂ = P₀ + 4T / b
The pressure difference across the common surface is:
P₁ - P₂ = 4T / R
Substitute P₁ and P₂:
(4T / a) - (4T / b) = 4T / R
Simplify:
1 / a - 1 / b = 1 / R
R = ab / (b - a)
Question 42:
A liquid is allowed to flow into a tube of truncated cone shape. Identify the correct statement:
View Solution
Solution:
From the principle of continuity:
A₁v₁ = A₂v₂
Here, A₁ and A₂ are the cross-sectional areas, and v₁ and v₂ are the velocities of the liquid at the wider and narrower ends, respectively.
Since A₁ > A₂, the velocity at the wider end (v₁) is lower than the velocity at the narrow end (v₂).
Question 43:
The velocity of sound in a gas in which two wavelengths 4.08 m and 4.16 m produce 40 beats in 12 seconds will be:
View Solution
The beat frequency is given by the formula:
fbeat = f₁ - f₂,
where f₁ and f₂ are the frequencies corresponding to the given wavelengths λ₁ and λ₂.
Step 1: Calculate the beat frequency
The beat frequency is:
fbeat = Number of beats ÷ Time = 40 ÷ 12 Hz.
Simplify:
fbeat = 10 ÷ 3 Hz.
Step 2: Relating wavelength to velocity and frequency
The frequency of a wave is related to its velocity by:
f = v ÷ λ.
Using the wavelengths λ₁ = 4.08 m and λ₂ = 4.16 m:
f₁ = v ÷ 4.08, f₂ = v ÷ 4.16.
Step 3: Solve for v
The beat frequency is:
fbeat = f₁ - f₂ = (v ÷ 4.08) - (v ÷ 4.16).
Simplify:
10 ÷ 3 = v × [(1 ÷ 4.08) - (1 ÷ 4.16)].
Calculate the difference in reciprocals:
(1 ÷ 4.08) - (1 ÷ 4.16) = (4.16 - 4.08) ÷ (4.08 × 4.16) = 0.08 ÷ 16.9728.
Substitute:
10 ÷ 3 = v × (0.08 ÷ 16.9728).
Solve for v:
v = [(10 ÷ 3) × 16.9728] ÷ 0.08 = 707.2 ms⁻¹.
Final Answer: 707.2 ms⁻¹
Question 44:
σ is the uniform surface charge density of a thin spherical shell of radius R. The electric field at any point on the surface of the spherical shell is:
View Solution
Using Gauss's law:
Electric flux = E × Area = Q / ε₀.
Step 1: Relate charge to surface charge density
The total charge Q on the spherical shell is:
Q = σ × 4πR².
Step 2: Simplify the electric field
The electric flux through a Gaussian surface of radius R is:
E × 4πR² = Q / ε₀.
Substitute Q = σ × 4πR² into the equation:
E × 4πR² = (σ × 4πR²) / ε₀.
Cancel 4πR² on both sides:
E = σ / ε₀.
Final Answer: σ / ε₀.
Question 45:
An electric field is given by E = (6i + 5j + 3k) N/C. The electric flux through a surface area of 30i m² lying in the YZ-plane (in SI units) is:
View Solution
The electric flux is calculated as:
Flux = E · A.
Here, A = 30i m² represents the area vector.
Substitute E = (6i + 5j + 3k):
Flux = (6i + 5j + 3k) · (30i).
Only the i-components contribute to the dot product:
Flux = 6 × 30 = 180.
Final Answer: 180.
Question 46:
A big drop is formed by coalescing 1000 small droplets of water. The surface energy will become:
View Solution
Step 1: Use volume conservation
(4/3)πR³ = 1000 × (4/3)πr³,
where R is the radius of the big drop, and r is the radius of each small drop.
Cancel (4/3)π:
R³ = 1000 × r³ → R = 10r.
Step 2: Compare surface energies
The initial surface energy is proportional to the surface area of 1000 small drops:
E₁ = 1000 × 4πr².
The final surface energy is proportional to the surface area of the big drop:
E₂ = 4πR² = 4π(10r)² = 100 × 4πr².
The ratio is:
E₂ / E₁ = (100 × 4πr²) / (1000 × 4πr²) = 1/10.
Final Answer: 1/10th.
Question 47:
If M is the mass of water that rises in a capillary tube of radius r, then the mass of water which will rise in a capillary tube of radius 2r is:
View Solution
The height of water in a capillary tube is given by:
h = (2T cos θ) / (r × ρ × g),
where T is surface tension, θ is the contact angle, ρ is the density of water, and g is gravitational acceleration.
The volume of water is:
V = πr² × h = πr² × [(2T cos θ) / (r × ρ × g)].
Simplify:
V ∝ r.
The mass of water is:
m = ρ × V ∝ r.
For a capillary of radius 2r:
m₂ = 2 × m₁.
Thus, the new mass is:
2M.
Question 48:
A closed organ pipe (closed at one end) is excited to support the third overtone. It is found that air in the pipe has:
View Solution
For a closed organ pipe, the length of the pipe for the n-th harmonic is given by:
L = [(2n - 1) × λ] / 4,
where λ is the wavelength.
For the third overtone:
n = 4.
The pipe supports four full loops plus a half loop, corresponding to:
4 nodes and 4 antinodes.
Question 49:
The electrostatic potential due to an electric dipole at a distance r varies as:
View Solution
The electrostatic potential V due to an electric dipole at a point at distance r from its center is proportional to:
V ∝ 1 / r³.
This is because the electric potential of a dipole decreases as the cube of the distance due to the nature of its charge distribution.
Question 50:
A battery of 6 V is connected to the circuit as shown below. The current I drawn from the battery is:
View Solution
The circuit contains a balanced Wheatstone bridge. The 5 Ω resistor does not contribute to the current as no current flows through it.
Step 1: Simplify the circuit
Remove the 5 Ω resistor and combine the remaining resistors.
- The two 3 Ω resistors in the top branch are in series: Rtop = 3 + 3 = 6 Ω.
- The two 6 Ω resistors in the bottom branch are in parallel: Rbottom = (6 × 6) / (6 + 6) = 3 Ω.
Combine Rtop and Rbottom in parallel:
Req = (6 × 3) / (6 + 3) = 18 / 9 = 2 Ω.
Add the 2 Ω resistor in series:
Rtotal = Req + 2 = 2 + 2 = 4 Ω.
Step 2: Apply Ohm's Law
Total current: I = V / Rtotal.
Substitute V = 6 V and Rtotal = 6 Ω:
I = 6 / 6 = 1 A.
Chemistry
Question 51:
If the length of the body diagonal of a FCC unit cell is x Å, the distance between two octahedral voids in the cell in Å is:
View Solution
In a FCC unit cell, octahedral voids are present at the body center and edge centers. The distance between two octahedral voids is:
- The body diagonal length is x = √3 × a, where a is the edge length.
- Edge length a = x / √3.
- The distance between octahedral voids is a / √2.
Substitute a = x / √3:
Distance = (x / √3) / √2 = x / √6.
Question 52:
Ortho-sulphobenzimide is used as:
View Solution
Ortho-sulphobenzimide is the chemical name for saccharin. It is widely used as a non-caloric artificial sweetener.
Question 53:
The volume of a gas at NTP is 1.12 × 10⁻⁷ cm³. The number of molecules in it is:
View Solution
At NTP, 22,400 cm³ of gas contains 6.02 × 10²³ molecules.
For a volume of 1.12 × 10⁻⁷ cm³:
Number of molecules = (6.02 × 10²³ / 22,400) × 1.12 × 10⁻⁷.
Number of molecules = (6.02 × 1.12 × 10²³ × 10⁻⁷) / 22,400.
Final result = 3.01 × 10¹² molecules.
Question 54:
The wavelength of radiation emitted, when a hydrogen atom electron falls from infinity to stationary state 1, would be: (Rydberg constant R = 1.097 × 10⁷ m⁻¹)
View Solution
The wavelength λ is calculated using the Rydberg formula:
1 / λ = R × (1 / n₁² - 1 / n₂²), where n₁ = 1 (final state) and n₂ = infinity (initial state).
- 1 / λ = R × (1 / 1²).
- Substitute R = 1.097 × 10⁷: 1 / λ = 1.097 × 10⁷.
- λ = 1 / (1.097 × 10⁷) = 91 nm.
Question 55:
In NO₃⁻ ion, the number of bond pairs and lone pairs of electrons on the nitrogen atom are:
View Solution
The structure of NO₃⁻ ion is:
O = N⁺ - O⁻ - O.
In NO₃⁻:
- The nitrogen atom forms 4 bond pairs (3 sigma bonds and 1 pi bond).
- The nitrogen atom has no lone pairs.
Question 56:
In which of the compounds does 'manganese' exhibit the highest oxidation number?
View Solution
In K₂MnO₄, the oxidation number of Mn can be calculated as:
2(+1) + x + 4(-2) = 0, where x is the oxidation number of Mn.
Simplify: 2 + x - 8 = 0 → x = +6.
In the other compounds:
- MnO₂: Mn = +4
- Mn₃O₄: Mn = +8/3 (average)
- MnSO₄: Mn = +2
Thus, the highest oxidation number is in K₂MnO₄.
Question 57:
Alkali metals are powerful reducing agents because:
View Solution
Alkali metals have a single valence electron, and their low ionisation energy makes it easy to lose this electron and get oxidised. This property makes them strong reducing agents.
Question 58:
A balloon filled with an air sample occupies 3 L volume at 35°C. On lowering the temperature to T, the volume decreases to 2.5 L. The temperature T is:
Assume pressure constant.
View Solution
From Charles's law:
V₁ / T₁ = V₂ / T₂.
Substitute the known values:
3 / 308 = 2.5 / T₂, where T₁ = 35°C = 273 + 35 = 308 K.
Solve for T₂:
T₂ = (2.5 × 308) / 3 = 256.6 K.
Convert to Celsius:
T₂ = 256.6 - 273 = -16.4°C ≈ -16°C.
Question 59:
Which one of the following is used as an eye lotion?
View Solution
Silver sol can be used as an eye lotion because of its antibacterial and healing properties. It helps in treating eye infections effectively.
Question 60:
Identify ortho and para directing groups from the following:
-CHO, -NHCOCH₃, -OCH₃, -SO₃H.
View Solution
Electron-donating groups like -NHCOCH₃ and -OCH₃ are ortho and para directing because they increase electron density at the ortho and para positions of the benzene ring through resonance or inductive effects.
Electron-withdrawing groups like -CHO and -SO₃H are meta directing.
Question 61:
Which one of the carbanions is the least stable?
View Solution
Carbanion stability depends on the electron-withdrawing nature of attached groups:
- -NO₂ and -CHO are strong electron-withdrawing groups, stabilising the negative charge.
- -CH₃ is electron-donating, which destabilises the negative charge.
Thus, CH₂-CH₃ is the least stable as it lacks electron-withdrawing groups.
Question 62:
In O₂⁻, O₂, and O₂²⁻ molecular species, the total number of antibonding electrons respectively are:
View Solution
The molecular orbital electronic configurations are:
- O₂⁻: π(2pₓ)² π(2pᵧ)² π*(2pₓ)¹ (7 antibonding electrons)
- O₂: π(2pₓ)² π(2pᵧ)² (6 antibonding electrons)
- O₂²⁻: π(2pₓ)² π(2pᵧ)² π*(2pₓ)² (8 antibonding electrons)
Question 63:
People living at high altitudes often reported a problem of feeling weak and inability to think clearly. The reason for this is:
View Solution
At high altitudes, the partial pressure of oxygen is lower, leading to reduced oxygen availability in the blood. This condition, called hypoxia, causes symptoms like weakness and difficulty in thinking, known as anoxia.
Question 64:
Specific conductance of 0.1 M HNO₃ is 6.3 × 10⁻² ohm⁻¹ cm⁻¹. The molar conductance of the solution is:
View Solution
Molar conductance is given by:
Λm = κ × (1000 / C),
where:
- κ = 6.3 × 10⁻² ohm⁻¹ cm⁻¹,
- C = 0.1 M.
Substitute:
Λm = 6.3 × 10⁻² × (1000 / 0.1) = 6.3 × 10² = 630 ohm⁻¹ cm² mol⁻¹.
Question 65:
The rate constant for a first-order reaction whose half-life is 480 seconds is:
View Solution
For a first-order reaction, the rate constant k is related to the half-life t1/2 as:
k = 0.693 / t1/2.
Substitute t1/2 = 480 s:
k = 0.693 / 480 = 1.44 × 10⁻³ s⁻¹.
Question 66:
If the activation energy for the forward reaction is 150 kJ/mol and that of the reverse reaction is 260 kJ/mol, what is the enthalpy change for the reaction?
View Solution
The enthalpy change ΔH for a reaction is related to the activation energies of the forward reaction (Eaf) and the reverse reaction (Ear) as:
ΔH = Eaf - Ear.
Substitute the given values:
ΔH = 150 - 260 = -110 kJ/mol.
Question 67:
For As₂S₃ sol, the most effective coagulating agent is:
View Solution
The coagulation of a negatively charged sol like As₂S₃ is most effective with a highly positively charged ion, as stated by the Hardy-Schulze rule.
Among the given options:
- FeCl₃ produces Fe³⁺, which has the highest positive charge (+3).
- Higher charges neutralise the negative charge of the sol more effectively, causing coagulation.
Other options, such as CaCO₃ (Ca²⁺) and NaCl (Na⁺), have lower positive charges and are less effective.
Question 68:
Element not showing variable oxidation state is:
View Solution
Fluorine is the most electronegative element and does not exhibit variable oxidation states because:
- It cannot expand its octet (no available d-orbitals).
- Fluorine always has an oxidation state of -1 in its compounds due to its high electronegativity.
Other halogens, such as bromine, iodine, and chlorine, can show variable oxidation states due to the presence of vacant d-orbitals.
Question 64:
Specific conductance of 0.1 M HNO₃ is 6.3 × 10⁻² ohm⁻¹ cm⁻¹. The molar conductance of the solution is:
View Solution
Molar conductance is given by:
Λm = κ × (1000 / C),
where:
- κ = 6.3 × 10⁻² ohm⁻¹ cm⁻¹,
- C = 0.1 M.
Substitute:
Λm = 6.3 × 10⁻² × (1000 / 0.1) = 6.3 × 10² = 630 ohm⁻¹ cm² mol⁻¹.
Question 65:
The rate constant for a first-order reaction whose half-life is 480 seconds is:
View Solution
For a first-order reaction, the rate constant k is related to the half-life t1/2 as:
k = 0.693 / t1/2.
Substitute t1/2 = 480 s:
k = 0.693 / 480 = 1.44 × 10⁻³ s⁻¹.
Question 66:
If the activation energy for the forward reaction is 150 kJ/mol and that of the reverse reaction is 260 kJ/mol, what is the enthalpy change for the reaction?
View Solution
The enthalpy change ΔH for a reaction is related to the activation energies of the forward reaction (Eaf) and the reverse reaction (Ear) as:
ΔH = Eaf - Ear.
Substitute the given values:
ΔH = 150 - 260 = -110 kJ/mol.
Question 67:
For As₂S₃ sol, the most effective coagulating agent is:
View Solution
The coagulation of a negatively charged sol like As₂S₃ is most effective with a highly positively charged ion, as stated by the Hardy-Schulze rule.
Among the given options:
- FeCl₃ produces Fe³⁺, which has the highest positive charge (+3).
- Higher charges neutralise the negative charge of the sol more effectively, causing coagulation.
Other options, such as CaCO₃ (Ca²⁺) and NaCl (Na⁺), have lower positive charges and are less effective.
Question 68:
Element not showing variable oxidation state is:
View Solution
Fluorine is the most electronegative element and does not exhibit variable oxidation states because:
- It cannot expand its octet (no available d-orbitals).
- Fluorine always has an oxidation state of -1 in its compounds due to its high electronegativity.
Other halogens, such as bromine, iodine, and chlorine, can show variable oxidation states due to the presence of vacant d-orbitals.
Question 69:
Which of the following arrangements does not represent the correct order of the property stated against it?
View Solution
Paramagnetic behaviour depends on the number of unpaired electrons:
- V²⁺: 3 unpaired electrons (3d³)
- Cr²⁺: 4 unpaired electrons (3d⁴)
- Mn²⁺: 5 unpaired electrons (3d⁵)
- Fe²⁺: 4 unpaired electrons (3d⁶)
The correct order is:
V²⁺ < Cr²⁺ < Fe²⁺ < Mn²⁺.
The given order in Option (1) is incorrect.
Question 70:
The IUPAC name for the complex [Co(ONO)(NH₃)₅]Cl₂ is:
View Solution
The complex contains:
- ONO (nitrito ligand coordinated through oxygen)
- NH₃ (neutral ammine ligands)
- Cl₂ (counter ions)
The oxidation state of cobalt is:
Co + 5(0) + (-1) + 2(-1) = 0 → Co = +3.
The name is:
Pentaammine-nitrito-O-cobalt(III) chloride.
Question 71:
Which of the following compounds will give a racemic mixture on nucleophilic substitution by OH⁻ ion?
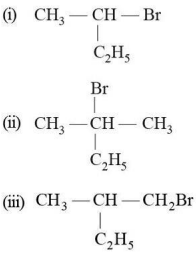
View Solution
Compounds undergoing the SN1 mechanism form a planar carbocation intermediate, allowing nucleophilic attack from both sides, resulting in a racemic mixture.
- Compound (i): Secondary carbon, follows SN1 mechanism.
- Compound (ii): Tertiary carbon, strongly favours SN1 mechanism.
- Compound (iii): Secondary carbon, follows SN1 mechanism.
All three compounds produce a racemic mixture.
Question 72:
Which one of the following is not correct for an ideal solution?
View Solution
Properties of an ideal solution:
- Obeys Raoult's law.
- No heat change during mixing (ΔH = 0).
- No volume change during mixing (ΔV = 0).
Option (3), stating ΔH = ΔV ≠ 0, is incorrect because both ΔH and ΔV must be zero for an ideal solution.
Question 73:
For the relation ΔrG = -nF Ecell, Ecell = E°cell, in which of the following conditions?
View Solution
For Ecell = E°cell, the Nernst equation is:
Ecell = E°cell - (RT/nF) ln Q,
where Q is the reaction quotient.
For Ecell = E°cell, ln Q must be zero, which occurs when:
Q = 1 → Concentration of all reactant and product species is unity.
Question 74:
Which one of the lanthanoids given below is the most stable in divalent form?
View Solution
The divalent state stability depends on the electronic configuration:
- Ce²⁺ → 4f¹
- Sm²⁺ → 4f⁶
- Eu²⁺ → 4f⁷ (half-filled, very stable)
- Yb²⁺ → 4f¹⁴ (fully filled, stable but less so than Eu²⁺)
Europium (Eu²⁺) is more stable due to its half-filled configuration.
Question 75:
The value of the 'spin only' magnetic moment for one of the following configurations is 2.84 BM. The correct one is:
View Solution
The spin-only magnetic moment is given by:
μ = √(n(n + 2)) BM, where n is the number of unpaired electrons.
Calculations for configurations:
- d⁵ (strong field): n = 1, μ = √3 = 1.73 BM
- d³ (any field): n = 3, μ = √15 = 3.87 BM
- d⁴ (weak field): n = 4, μ = √24 = 4.89 BM
- d⁴ (strong field): n = 2, μ = √8 = 2.84 BM
The correct configuration is d⁴ in strong ligand fields.
Question 76:
Chlorobenzene reacts with Mg in dry ether to give a compound (A) which further reacts with ethanol to yield:
View Solution
Step 1: Chlorobenzene (C₆H₅Cl) reacts with Mg in dry ether to form phenyl magnesium chloride (C₆H₅MgCl).
Step 2: Phenyl magnesium chloride reacts with ethanol (C₂H₅OH) to produce benzene (C₆H₆) and magnesium ethoxide (C₂H₅OMgCl).
Question 78:
Which of the following represents the correct order of acidity in the given compounds?
View Solution
Acidity in carboxylic acids is increased by electron-withdrawing (-I) groups.
Order of electronegativity: F > Cl > Br > H.
Fluorine has the strongest -I effect, stabilizing the carboxylate ion and increasing acidity, followed by chlorine, bromine, and hydrogen.
Question 79:
Ethyl alcohol can be prepared from Grignard reagent by the reaction of:
View Solution
Grignard reagents react with carbonyl compounds to form alcohols. Formaldehyde (HCHO) reacts with Grignard reagents to produce primary alcohols like ethyl alcohol (C2H5OH).
Step 1: Reaction mechanism.
1. The nucleophilic CH3MgBr attacks the electrophilic carbon in formaldehyde:
HCHO + CH3MgBr → CH3CH2OMgBr.
2. The intermediate alcoholate ion (CH3CH2OMgBr) is hydrolyzed to form ethyl alcohol:
CH3CH2OMgBr + H3O+ → CH3CH2OH.
Question 80:
Which of the following is most acidic?
View Solution
Phenols are more acidic than alcohols because the phenoxide ion formed after losing H+ is resonance stabilized. Among phenols, electron-withdrawing substituents like -Cl increase acidity by stabilizing the negative charge on the oxygen atom.
Step 1: Compare structures.
Benzyl alcohol: Less acidic because the -OH group is attached to a saturated carbon.
Cyclohexanol: Similar to benzyl alcohol, it lacks resonance stabilization.
Phenol: Acidic due to resonance stabilization of the phenoxide ion.
m-Chlorophenol: Most acidic because the -Cl group has an electron-withdrawing (-I) effect, enhancing resonance stabilization.
Question 81:
Nitration of the compound is carried out. This compound gives a red-orange precipitate with 2,4-DNP, undergoes Cannizzaro reaction but not aldol, then the possible product due to nitration is:
View Solution
The compound undergoes Cannizzaro reaction but not aldol condensation, indicating the absence of alpha-hydrogens. This suggests that the compound is an aldehyde. Upon nitration, benzaldehyde forms 3-nitrobenzaldehyde.
Step 1: Reaction mechanism.
CHO → NO2-CHO (meta-nitrobenzaldehyde).
The nitration occurs at the meta-position relative to the aldehyde group due to the electron-withdrawing nature of the -CHO group.
Question 82:
Which of the following reactions will not give a primary amine?
View Solution
The reactions and their respective products are:
(a) Hofmann Bromamide Reaction: CH3CONH2 + Br2 + KOH → CH3NH2 (Primary Amine)
(b) Reduction of Nitriles: CH3CN + LiAlH4 → CH3CH2NH2 (Primary Amine)
(c) Reduction of Isocyanides: CH3NC + LiAlH4 → CH3NHCH3 (Secondary Amine)
(d) Reduction of Amides: CH3CONH2 + LiAlH4 → CH3CH2NH2 (Primary Amine)
Conclusion: Only reaction (3) produces a secondary amine and does not yield a primary amine.
Question 83:
Which of the following compounds is most reactive towards nucleophilic addition reactions?
View Solution
Nucleophilic addition reactivity depends on steric hindrance and the electrophilicity of the carbonyl carbon.
- Aldehydes: Less steric hindrance and more electrophilic than ketones.
- Acetaldehyde: Minimal steric hindrance and no resonance effects, making it the most reactive.
- Ketones and benzophenone: Steric hindrance from two substituents reduces reactivity.
- Benzaldehyde: Resonance of the phenyl group decreases electrophilicity.
Conclusion: Acetaldehyde (CH3CHO) is the most reactive compound.
Question 84:
Molecules whose mirror image is non-superimposable over them are known as chiral. Which of the following molecules is chiral in nature?
View Solution
A molecule is chiral if it has at least one carbon atom bonded to four different groups.
- 2-Bromobutane: Contains a chiral carbon bonded to bromine, hydrogen, a methyl group, and an ethyl group.
- 1-Bromobutane: The first carbon is bonded to two identical hydrogen atoms, making it achiral.
- 2-Bromopropane: The second carbon is bonded to two identical methyl groups, making it achiral.
- 2-Bromopropan-2-ol: The second carbon is bonded to two identical methyl groups, making it achiral.
Conclusion: Only 2-bromobutane is chiral.
Question 85:
The most reactive amine towards dilute hydrochloric acid is:
View Solution
The basicity of amines depends on the inductive effect and steric hindrance:
- Methylamine: A primary amine with moderate basicity.
- Dimethylamine: A secondary amine with strong inductive effects and minimal steric hindrance, making it the most basic.
- Trimethylamine: A tertiary amine with strong inductive effects but steric hindrance reduces reactivity.
- Aniline: Resonance of the aromatic ring reduces its basicity, making it the least reactive.
Conclusion: Dimethylamine reacts most readily with dilute hydrochloric acid.
Question 86:
One of essential alpha-amino acids is:
View Solution
Essential amino acids cannot be synthesized by the human body and must be obtained through diet. Lysine is one such essential amino acid critical for protein synthesis and other metabolic functions.
Serine, glycine, and proline are non-essential amino acids because they can be synthesized by the body.
Question 87:
Which of the following statements is true about a peptide bond (RCONHR')?
View Solution
A peptide bond is covalent and planar due to resonance. It can form hydrogen bonds because the NH group acts as a donor and the CO group acts as an acceptor.
- Option (1): Incorrect as the peptide bond is planar.
- Option (2): Correct because of hydrogen bond capability.
- Option (3): Incorrect, as the trans configuration is more stable due to reduced steric hindrance.
- Option (4): Incorrect, as rotation is restricted by partial double-bond character.
Question 88:
Which of the following is an example of chain-growth polymer?
View Solution
Chain-growth polymerization involves the successive addition of monomers, typically through free radicals or ions. Teflon is formed by the polymerization of tetrafluoroethylene, making it a chain-growth polymer.
- Bakelite, Nylon, and Terylene are step-growth polymers, formed by condensation reactions.
Question 89:
Which of the following polymers is formed due to the co-polymerization of 1,3-butadiene and phenylethene?
View Solution
Buna-S is formed by the co-polymerization of 1,3-butadiene and phenylethene (styrene). Other polymers are:
- Buna-N: Co-polymer of 1,3-butadiene and acrylonitrile.
- Neoprene: Polymer of chloroprene.
- Novolac: Phenol-formaldehyde resin.
Question 90:
For 1 molal aqueous solution of the following compounds, which one will show the highest freezing point?
View Solution
The freezing point depends on the number of particles (i) formed upon dissociation:
- (1) Dissociates into 4 particles.
- (2) Dissociates into 3 particles.
- (3) Dissociates into 2 particles.
- (4) Does not dissociate (1 particle).
The compound with the fewest particles ([Co(H2O)3Cl3]·3H2O) will have the highest freezing point.
Question 91:
Which of the following expressions correctly represents molar conductivity?
View Solution
Molar conductivity (Λm) is defined as the conductance of all ions in 1 mole of solution, placed between two electrodes of unit area separated by unit distance. All given formulas are valid representations:
- Λm = K / C: Relates molar conductivity to conductivity (K) and molar concentration (C).
- Λm = (K × A) / l: Derived from conductance G and the relationship to molar conductivity, where A is the area, and l is the electrode separation.
- Λm = K × V: Relates molar conductivity to conductivity and solution volume V.
Question 92:
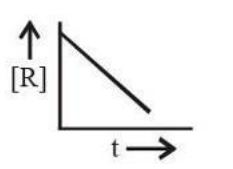
The plot that represents the zero-order reaction is:
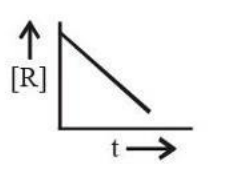
View Solution
For a zero-order reaction, the rate law is r = k, and the integrated rate equation is:
[R] = [R]0 - kt.
This equation represents a straight line with a negative slope (-k) when [R] is plotted against t. Thus, the correct graph is a linear plot with a downward slope.
Question 93:
In acidic medium, which of the following does not change its colour?
View Solution
In acidic conditions:
- MnO4- retains its purple color.
- MnO42- disproportionates to MnO4- and Mn2+.
- CrO42- converts to Cr2O72-, changing from yellow to orange.
- FeO42- decomposes to Fe3+, losing its color.
Thus, MnO4- does not change its color in acidic medium.
Question 94:
Which of the following is the life-saving mixture for an asthma patient?
View Solution
Heliox (a mixture of helium and oxygen) is used to treat asthma patients. Helium reduces airway resistance due to its low density, making it easier for patients to breathe.
Question 95:
The compounds [PtCl2(NH3)4]Br2 and [PtBr2(NH3)4]Cl2 constitute a pair of:
View Solution
These compounds differ in the exchange of anions between the inner and outer spheres:
- [PtCl2(NH3)4]Br2: Chloride ions are in the coordination sphere, bromide ions in the outer sphere.
- [PtBr2(NH3)4]Cl2: Bromide ions are in the coordination sphere, chloride ions in the outer sphere.
These are ionization isomers as they differ in the anion present in the coordination sphere.
Question 96:
Tincture of iodine is the common name for:
View Solution
Tincture of iodine is a solution of iodine (2-3%) in alcohol and water, commonly used as an antiseptic. The alcohol acts as a solvent, and the iodine provides antimicrobial properties. Other options like iodoform, 2-iodopropane, and iodobenzene are unrelated to tincture.
Question 97:
The monomers of Buna-S rubber are:
View Solution
Buna-S rubber is formed by the copolymerization of butadiene (CH2=CH-CH=CH2) and styrene (C6H5-CH=CH2). It is widely used in making automobile tires due to its durability and resistance to abrasion.
Question 98:
The number of nearest neighbours in a BCC unit cell is:
View Solution
In a Body-Centered Cubic (BCC) structure, the atom at the center touches the eight corner atoms, making the coordination number 8. Other coordination numbers are incorrect for BCC: 12 applies to FCC, 6 to simple cubic, and 4 does not apply.
Question 99:
The cell potential for the following cell is approximately:
M(s) | M3+(aq, 0.1M) || N2+(aq, 0.1M) | N(s)
E0M3+/M = 0.6 V, E0N2+/N = 0.1 V.
View Solution
Using the Nernst equation:
Ecell = E0cell - (0.059/n) log Q.
After calculating with Q = (0.01)2/(0.1)3, the cell potential is approximately 0.51 V.
Question 100:
In Williamson synthesis, if tertiary alkyl halide is used, then:
View Solution
Tertiary alkyl halides predominantly undergo elimination (E2 mechanism) due to steric hindrance, forming alkenes instead of ethers. For example:
(CH3)3C-Br + CH3O- → (CH3)2C=CH2 + CH3OH + NaBr.
Question 101:
If A = [[1, 0], [1/2, 1]], then A50 is:
View Solution
We calculate powers of A:
A2 = [[1, 0], [1/2, 1]] × [[1, 0], [1/2, 1]] = [[1, 0], [1, 1]].
A4 = A2 × A2 = [[1, 0], [1, 1]] × [[1, 0], [1, 1]] = [[1, 0], [2, 1]].
From this pattern, A50 = [[1, 0], [50, 1]].
Thus, the given options do not match the result.
Question 102:
The range of the function f(x) = sin-1(x - √x) is equal to:
View Solution
The function is f(x) = sin-1(x - √x).
Step 1: Analyze g(x) = x - √x. For x ∈ [0, 1], the range of g(x) is [-1/4, 1].
Step 2: Apply sin-1. The range of f(x) is [-sin-1(1/4), π/2].
Question 103:
If a = i + 2j - 3k and b = 2i - 3j - 5k, then:
View Solution
Compute a - b = [-i + 5j + 2k]. Magnitude: |a - b| = √30. For |a| = √14 and |b| = √38, verify that |a - b| > |b| - |a|.
Question 104:
If √(y/x) + 4√(x/y) = 4, then dy/dx:
View Solution
Simplify the given equation: y² + 16x² = 8xy. Differentiate both sides and solve for dy/dx. Result: dy/dx = 4.
Question 105:
The function f(x) = tan-1(sin x + cos x) is an increasing function in:
View Solution
Differentiate f(x): f'(x) = √2 cos(x + π/4)/(1 + (sin x + cos x)²). f'(x) > 0 in (-π/2, π/4).
Question 106:
If f(x) = |x| - |1|, then points where f(x) is not differentiable, is/are:
View Solution
The function f(x) = ||x| - 1| has sharp edges at x = -1, 0, and 1. These points are where the function is non-differentiable.
Question 107:
The integral ∫(π/11 to 9π/22) dx / (1 + √(tan x)) is equal to:
View Solution
Using substitution x → π/2 - x, the integral simplifies. Adding the original and substituted integrals results in the evaluation of limits and symmetry properties, yielding 7π/44.
Question 108:
Let a = i + 2j + k, b = i - j + k, and c = i + j - k. A vector in the plane of a and b whose projection on c is 1/√3, is:
View Solution
A vector in the plane of a and b is u = a + λb. Solving for the projection condition on c using projection formula gives the vector 4i - j + 4k.
Question 109:
Let p: "I am brave," q: "I will climb Mount Everest." The symbolic form of the statement "I am neither brave nor I will climb Mount Everest" is:
View Solution
The statement "neither brave nor climb Mount Everest" corresponds to "not brave and not climbing," represented symbolically as ~p ∧ ~q.
Question 110:
If x ≠ 0, then
(sin(π + x) * cos(π/2 + x) * tan(3π/2 - x) * cot(2π - x)) / (sin(2π - x) * cos(2π + x) * csc(-x) * sin(3π/2 + x)) =
View Solution
Simplifying each trigonometric term using identities like sin(π + x) = -sin(x) and cos(π/2 + x) = -sin(x), and substituting into the given expression, results in a final value of 1.
Question 111:
Evaluate i² + i³ + ... + i⁴⁰⁰⁰:
View Solution
The powers of i cycle every 4 terms: i, -1, -i, 1. Grouping terms into 1000 complete cycles and adding the remaining terms gives a result of -i.
Question 112:
The number of all four-digit numbers which begin with 4 and end with either 0 or 5 is:
View Solution
Fix the first digit as 4 and the last digit as either 0 or 5. The second and third digits can take any value from 0 to 9, resulting in 200 valid numbers.
Question 113:
The number of ways of distributing 500 dissimilar boxes equally among 50 persons is:
View Solution
To distribute 500 dissimilar boxes equally among 50 people, each receiving 10 boxes, the total arrangements are 500! divided by (10!)⁵⁰ for the internal arrangement of each group.
Question 114:
Given, the function f(x) = (aˣ + a⁻ˣ) / 2 (a > 2), then f(x + y) + f(x - y) is equal to:
View Solution
Using the definitions of f(x + y) and f(x - y) and simplifying with exponential rules, the result is 2f(x)f(y).
Question 115:
The point on the line 4x - y - 2 = 0 which is equidistant from the points (-5, 6) and (3, 2) is:
View Solution
Using the condition of equidistance and substituting into the line equation, the coordinates of the point are calculated as (4, 14).
Question 116:
The equation of a circle with center (5, 4) and touching the Y-axis is:
View Solution
The circle's center is at (5, 4), and the radius is the distance from the center to the Y-axis, which equals 5. The equation is derived as \( (x - 5)² + (y - 4)² = 5² \). Simplified, it becomes \( x² + y² - 10x - 8y + 16 = 0 \).
Question 117:
Evaluate the following limit:

View Solution
The given limit is:
Limit as theta approaches -pi/4 of (cos(theta) + sin(theta)) / (theta + pi/4).
Step 1: Simplify the denominator.
Let h = theta + pi/4. Then, as theta approaches -pi/4, h approaches 0. The expression becomes:
Limit as h approaches 0 of (cos(pi/4 - h) + sin(pi/4 - h)) / h.
Step 2: Simplify the numerator using trigonometric identities.
Expand cos(pi/4 - h) and sin(pi/4 - h):
cos(pi/4 - h) = cos(pi/4) * cos(h) + sin(pi/4) * sin(h),
sin(pi/4 - h) = sin(pi/4) * cos(h) - cos(pi/4) * sin(h).
Adding these:
cos(pi/4 - h) + sin(pi/4 - h) = (cos(pi/4) + sin(pi/4)) * cos(h) + (sin(pi/4) - cos(pi/4)) * sin(h).
Since cos(pi/4) = sin(pi/4) = 1/sqrt(2), this simplifies to:
cos(pi/4 - h) + sin(pi/4 - h) = sqrt(2) * cos(h).
Step 3: Evaluate the limit.
Substitute back into the limit:
Limit as h approaches 0 of (sqrt(2) * cos(h)) / h.
As h approaches 0, cos(h) approaches 1. The limit becomes:
sqrt(2).
Question 119:
If two numbers ( p ) and ( q ) are chosen randomly from the set {1, 2, 3, 4} with replacement, what is the probability that ( p² ≥ 4q )?
View Solution
Calculate total possible outcomes as 16. Identify 7 favorable outcomes where \( p² ≥ 4q \). Probability is \( 7/16 \).
Question 120:
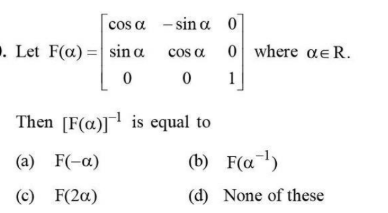
View Solution
The inverse of a rotation matrix is its transpose. Hence, \( F(α)⁻¹ = F(-α) \), which satisfies the rotation matrix properties.
Question 121:
Let vectors a, b, and c be non-zero such that (a × b) ⋅ c = (1/3) × |b| × |c| × |a|. If θ is the acute angle between b and c, find sin θ.
View Solution
From the given equation, we use the scalar triple product formula. After solving, we find that cos θ = -1/3. Using the identity sin²θ + cos²θ = 1, we find sin θ = 2√2 / 3.
Question 122:
Find the distance of the foot of the perpendicular from (1, 2, 4) to the plane 3x + 4y + 12z + 23 = 0, given that it lies on the line (x + 2) / 4 = (y - 1) / 2 = (z + 1) / 3.
View Solution
Using parametric equations of the line, we find the coordinates of the foot of the perpendicular. Then, using the formula for the distance from a point to a plane, the calculated distance is 5.
Question 123:
If one of the lines given by 6x² - xy + 4cy² = 0 is 3x + 4y = 0, find the value of c.
View Solution
Substitute y = -(3/4)x into the given equation and solve for c. Simplification leads to c = -3.
Question 124:
If x = a(cos θ + θ sin θ) and y = a(sin θ - θ cos θ), find d²y / dx².
View Solution
Compute dx/dθ and dy/dθ, then find dy/dx. Finally, differentiate dy/dx with respect to θ and simplify. The result is sec³θ / (aθ).
Question 125:
Find the absolute maximum value of f(x) = 2x³ - 3x² - 36x + 9 on [-3, 3].
View Solution
Find the critical points by solving f'(x) = 0. Evaluate f(x) at the critical points and endpoints. The maximum value is 53.
Question 126:
Define f(x) = {x² + bx + c for x < 1, x for x ≥ 1}. If f(x) is differentiable at x = 1, then b - c is equal to:
View Solution
At x = 1, continuity gives 1 + b + c = 1, so b + c = 0. Differentiability gives 2x + b = 1 at x = 1, which means b = -1. From b + c = 0, we find c = 1. Therefore, b - c = -1 - 1 = -2.
Question 127:
The Boolean expression (~(p ∧ q)) ∨ q is equivalent to:
View Solution
Simplify the Boolean expression using De Morgan's laws and distributive properties. The result is equivalent to p → (p ∨ q).
Question 128:
If x = (1 - t²) / (1 + t²) and y = (2t) / (1 + t²), find dy/dx:
View Solution
Using the parametric relations x = cos(2θ) and y = sin(2θ), the derivative dy/dx simplifies to -x / y.
Question 129:
The tangent at point (x₁, y₁) on the curve y = x³ + 3x² + 5 passes through the origin. Find the curve where (x₁, y₁) does NOT lie:
View Solution
Find the tangent equation and verify the given curves. The point (x₁, y₁) does not satisfy (x / 3) - y² = 2.
Question 130:
Evaluate the integral of [x sin⁻¹(x)] / √(1 - x²) with respect to x:
View Solution
Using substitution sin⁻¹(x) = t, the integral simplifies to x - √(1 - x²) sin⁻¹(x) + C.
Question 131:
The value of the integral of (x + 1) / (x(1 + xe^x)) with respect to x is:
View Solution
Using the substitution xe^x = t, we simplify the integral to integrate (1/t - 1/(1 + t)) with respect to t. After integration, substituting back t = xe^x gives the final result: log | (xe^x) / (1 + xe^x) | + C.
Question 132:
The order and degree of the differential equation √(dy/dx) - 4(dy/dx) - 7x = 0 are:
View Solution
Squaring the equation removes the square root, resulting in an equation with the highest order derivative dy/dx raised to the second power. Therefore, the order is 1, and the degree is 2.
Question 133:
Given vectors a = i + j + k, b = i + 3j + 5k, and c = 7i + 9j + 11k, the area of a parallelogram with diagonals a + b and b + c is:
View Solution
Calculate the cross product of the diagonals, then divide by 2 to find the parallelogram's area. The magnitude of the result gives the final answer: 4√6 square units.
Question 134:
If X is a random variable with P(X = -2) = P(X = -1) = P(X = 1) = P(X = 2) = 1/6 and P(X = 0) = 1/3, the mean of X is:
View Solution
The mean is calculated as the sum of all possible values of X multiplied by their probabilities. Here, the sum simplifies to 0.
Question 135:
Evaluate the integral of e^x (2 + sin(2x)) / (1 + cos(2x)) with respect to x:
View Solution
Using trigonometric identities, simplify the integrand into a sum of two simpler terms. Solve each integral to obtain e^x tan(x) + C as the final answer.
Question 136:
The solution of the differential equation y² dx + (x² - xy + y²) dy = 0 is:
View Solution
Divide the equation by y², substitute x = vy, and simplify. Separate the variables and integrate both sides, resulting in arctan(x/y) + ln(y) + C = 0.
Question 137:
Two lines given by the vector equations r₁ = (2i - 3j + 7k) + λ(2i + pj + 5k) and r₂ = (i + 2j + 3k) + μ(3i - pj + pk) are perpendicular for all λ and μ. The value of p is:
View Solution
Perpendicular lines have direction vectors with a dot product equal to zero. Compute the dot product of the direction vectors (2i + pj + 5k) and (3i - pj + pk), set it to zero, and solve for p. The solution gives p = 6.
Question 138:
Evaluate sin(tan⁻¹(4/5) + tan⁻¹(4/3) + tan⁻¹(1/9) - tan⁻¹(1/7)):
View Solution
Simplify the expression using the formula for adding and subtracting arctangents. Combine terms to get sin(π/2), which equals 1.
Question 139:
Let f(x) = (2 - √(x + 4)) / sin(2x), x ≠ 0. For f(x) to be continuous at x = 0, f(0) must be defined as:
View Solution
To ensure continuity, find the limit of f(x) as x approaches 0. Apply L’Hôpital’s Rule to resolve the indeterminate form and determine f(0) = -1/8.
Question 140:
Evaluate the integral ∫ from 0 to π/4 of (cos²(x) / (cos²(x) + 4sin²(x))) dx:
View Solution
Substitute tan(x) = t, transform the integral, and simplify. Compute partial fractions and integrate to get the result: -π/12 + (2/3) arctan(2).
Question 141:
The area of the region described by {(x, y) | x² + y² ≤ 1 and y² ≤ 1 - x} is:
View Solution
The region is bounded by the circle x² + y² = 1 and the parabola y² = 1 - x. The total area is computed as A = 2∫[0 to 1] √(1 - x²) dx + ∫[0 to 1] √(1 - x) dx. Solving the integrals gives the final result as π/2 + 4/3.
Question 142:
Two players A and B alternately throw a coin and a die. The first to throw both a head and a 6 wins. If A starts, the probability that B wins is:
View Solution
The probability of throwing both a head and a 6 is 1/12. Using geometric progression for alternating events, the probability that B wins is calculated as 11/23.
Question 143:
Consider the system of equations: kx + y + z = 1, x + ky + z = k, x + y + kz = k². Find |k| if the system has no solution:
View Solution
The determinant of the coefficient matrix is calculated as k³ - 3k + 2. For the system to have no solution, the determinant must be zero, leading to k = 2 or -2. Thus, |k| = 2.
Question 144:
If f(x) is differentiable at x = 1, and limit as h approaches 0 of (1/h)f(1 + h) = 5, then f'(1) is:
View Solution
Using the definition of a derivative, the given limit simplifies to f'(1) = 5.
Question 145:
The area of the region {(x, y): 0 ≤ y ≤ x² + 1, 0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} is:
View Solution
The given region is divided into two parts based on boundaries. For x between 0 and 1, the top boundary is y = x² + 1. For x between 1 and 2, the top boundary is y = x + 1. The areas are computed as ∫[0 to 1] (x² + 1) dx + ∫[1 to 2] (x + 1) dx, resulting in a total area of 23/6.
Question 146:
The solution of the differential equation √(1 - y²) dx + x dy - sin⁻¹(y) dy = 0 is:
View Solution
The given equation is rearranged as √(1 - y²) dx = (sin⁻¹(y) - x) dy. Dividing by √(1 - y²), the equation becomes dx = (sin⁻¹(y) - x)/√(1 - y²) dy. Using an integrating factor e^(sin⁻¹(y)), the solution is derived as x = sin⁻¹(y) - 1 + ce^(-sin⁻¹(y)).
Question 147:
Let X be a discrete random variable representing the number rolled on a biased die. The probability distribution of X is:
X = {1, 2, 3, 4, 5, 6}
P(X = x) = {0.1, 0.15, 0.3, 0.25, k, k}
The variance of X is:
View Solution
Total probability is 1. Solve for k: 0.1 + 0.15 + 0.3 + 0.25 + 2k = 1, which gives k = 0.1. Calculate the mean μ = Σ(X * P(X)) = 3.4. Calculate E(X²) = Σ(X² * P(X)) = 13.5. Variance is E(X²) - μ² = 13.5 - 11.56 = 1.93.
Question 148:
If the vector equation of the line (x - 2)/2 = (2y - 5)/-3 = z + 1 is rewritten as:
r = (2i + 5/2j - k) + λ(2i - 3/2j + pk)
Then p is equal to:
View Solution
The line passes through the point (2, 5/2, -1) with direction ratios (2, -3/2, 0). The z-component of the direction vector must be 0, so p = 0.
Question 149:
Which of the following is correct?
View Solution
If A is symmetric, then (B'AB)' = B'A'B = B'AB. Therefore, B'AB is symmetric.
Question 150:
A spherical iron ball with a radius of 10 cm is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm³/min. When the thickness of the ice is 15 cm, the rate at which the thickness of the ice decreases is:
View Solution
Volume rate of change is dV/dt = 50. Volume of the sphere is (4/3)πr³. Differentiate to find dr/dt: 4πr²(dr/dt) = 50. Substituting r = 15 gives dr/dt = 1/(18π).
Also Check:
MHT CET Previous Year Question Papers
| MHT CET 2023 Question Paper | MHT CET 2022 Question Paper |
| MHT CET 2021 Question Paper | MHT CET 2020 Question Paper |
| MHT CET 2019 Question Paper | MHT CET 2018 Question Paper |
Also Check:








Comments