
Arpita Srivastava Content Writer
Content Writer
- Linear Programming is also known as linear optimisation or LP.
- It satisfies conditions like variables are non-negative.
- The method satisfies a collection of linear inequalities (also referred to as linear constraints).
- The variables are sometimes called decision variables and are non-negative.
- It solves manufacturing problems, diet problems and transportation problems.
- It is used to depict real-world relationships by analysing the situation.
- Linear Programming objective function is given as
z = px + qy
- where programming constraints that satisfies the given condition is as follows: x ≥ 0, y ≥ 0
Read More: Difference between Variables and Constants
Key Terms: Linear Programming, Variables, Linear Equation, Corner Points, Graphical Method, Function, Profit, Constraints, Linear Inequalities, Vertex
What is Linear Programming?
[Click Here for Sample Questions]
Linear Programming is a method that is used to determine the maximum profit or minimum cost value in any mathematical model. It is also referred to as a primal problem that is used to solve dual problems.
- Linear Programming solves a problem with a limited amount of resources.
- The graph of any linear equation has two variables.
- To verify the equation, we need to plot coordinate points.
- In linear programming, we have two or more simultaneous linear equations.
- Next, we need to find the range of the solutions from the given conditions.
Solved Example of Linear ProgrammingQues. (Allocation problem) A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The take advantage of crops X and Y per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. to regulate weeds, a liquid herbicide has got to be used for crops X and Y at rates of 20 litres and 10 litres per hectare. Further, not quite 800 litres of herbicide should be utilized in order to guard fish and wildlife employing a pond which collects drainage from this land. what proportion land should be allocated to every crop so as to maximise the entire profit of the society? Ans.Let x hectare of land be allocated to crop X and y hectare of land be allocated to crop Y. Since x and y can not be zero. So, x ≥ 0, y ≥ 0. Profit per hectare On crop X = Rs 10500 And on crop Y = Rs 9000 Therefore, total profit = Rs (10500x + 9000y) Maximise Z = 10500 x + 9000 y subject to the constraints: constraint associated with land x + y ≤ 50 ... (1) constraint associated with use of herbicide 20x + 10y ≤ 800 ⇒2x + y ≤ 80 ... (2) x ≥ 0, y ≥ 0 ... (3) By plotting the graph of inequalities (1) to (3). We get the feasible region OABC. We can see that the feasible region is bounded and the coordinates at the corner points O, A, B and C are (0, 0), (40, 0), (30, 20) and (0, 50) respectively. Now evaluate the function Z = 10500 x + 9000y at these corner points to get the maximum profit.  Hence, the maximum profit attained at point B (30,20). So, the society will get the maximum profit of Rs 4,95,000 by allocating 30 hectares for crop X and 20 hectares for crop Y. Read More: Linear Equation in Two Variables |
Types of Linear Programming
[Click Here for Sample Questions]
There are three types of problems that are the most common in linear programming, which are as follows:
Manufacturing Problem
In manufacturing problems, we maximize the profit with the help of minimum utilization of resources.
Solved Example of Manufacturing ProblemQues. (Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at the most 12 hours whereas machine III must be operated for a minimum of 5 hours each day . She produces only two items M and N each requiring the utilization of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given in the following table: Ans. Let x and y be the amount of things M and N respectively. Now total profit will be = Rs (600 x + 400 y) So we can say Maximise Z = 600 x + 400 y subject to the constraints: x + 2y ≤ 12 ...(1) 2x + y ≤ 12 ... (2) x + 5 4 y ≥ 5 ... (3) x ≥ 0, y ≥ 0 ... (4) From the graph determined by the constraints (1) to (4), we get the ABCDE as the feasible region (shaded). We can see the feasible region is bounded and the coordinates of the corner points A, B, C, D and E are (5, 0) (6, 0), (4, 4), (0, 6) and (0, 4) respectively. Let us evaluate Z = 600 x + 400 y at these corner points.
We can see that the corner point C (4, 4) is giving the maximum value of Z. Hence, the manufacturer has to produce 4 units of every item to get the maximum profit of Rs 4000. |
Diet Problem
In diet problems, we calculate the number of various nutrients in a diet to reduce the cost of manufacturing.
Solved Example of Diet ProblemQues. (Diet problem): A dietician wishes to mix two types of foods in such a way that vitamin contents of the mixture contain atleast 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C . Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 50 per kg to get Food ‘I’ and Rs 70 per kg to get Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture? Ans.Let the mixture have x kg of Food ‘I’ and y kg of Food ‘II’. Since, x and y can not be zero So, x ≥ 0, y ≥ 0. From given data-
Given that the mixture should contain at least 8 units of vitamin A and 10 units of vitamin C. So, get the constraints: 2x + y ≥ 8 x + 2y ≥ 10 Let total cost of x kg of food ‘I’ and y kg of Food ‘II’ be Z so, Z = 50x + 70y Hence, we get: Minimise Z = 50x + 70y ... (1) Subject to the constraints: 2x + y ≥ 8 … (2) x + 2y ≥ 10 ... (3) x, y ≥ 0 ... (4) By plotting the graph between the inequalities (2) to (4).
Here the feasible region is unbounded. So we have to evaluate Z at points A(0,8), B(2,4) and C(10,0) In the table, we can see the smallest value of Z is 380 at the point (2,4). So we can say that the minimum value of Z is 380. Since, the feasible region is unbounded. So, we have to draw the graph of the inequality 50x + 70y < 380 ⇒5x + 7y < 38 From the graph we can see that it has no points in common. Thus, the minimum value of Z is 380 at the corner points (2, 4). Hence, the dietician needs to combine 2 kg of Food ‘I’ and 4 kg of Food ‘II’, and with this strategy, the minimum cost of the mixture will be Rs 380. |
Transportation Problem
In transportation problems, we calculate the schedule to find the cheapest and easiest way of transporting a product in less time.
Read More:
| Chapter Related Concepts | ||
|---|---|---|
| Differential Equation | First Order Differential Equation | Difference between Sequence and Series |
| Definite Integral Formula | Differentiation and Integration Formula | |
Characteristic of Linear Programming
[Click Here for Sample Questions]
There are many terms which are commonly used in linear programming. They are listed below:
Objective function
A linear function (z = px + qy, where p and q are constants) whose value is either to be maximized or minimized is known as the objective function.
Constraints
The linear inequations or inequalities on the variables of the linear programming problem (LPP) are called constraints. The conditions where x ≥ 0 and y ≥ 0 are called non-negative restrictions.
Optimal Value
Every objective function has either a maximum value or a minimum value. So, the value of the objective function is named as the optimal value.
Optimization Problem
A problem which is about maximizing or minimizing a linear function subject to constraints, as determined by a set of linear inequalities, is called an optimization problem.
Feasible Region
A common region which is found by all constraints, including non-negative constraints of an LP, is known as a feasible region. The feasible region is also referred to as a convex polygon. At the same time, the region apart from the feasible region is known as an infeasible region.
Read More: Eccentricity
Feasible Solutions
Points on the boundary of the feasible region show the feasible solutions of the constraints. Any point outside the feasible region is named an infeasible solution.
Optimal Feasible Solution
Any point in the feasible region that shows the optimal value of the objective function is called the optimal feasible solution.
Bounded and Unbounded Region
If a feasible region of a linear inequality is enclosed within a circle, then it’s a bounded region; otherwise, it is an unbounded region.
Read More: Eccentric Formula
Theorem of Linear Programming
[Click Here for Sample Questions]
The two important theorem of linear programming are as follows:
Theorem 1
Let R be the feasible region for a linear programming problem and let z = ax + by be the objective function. Z has an optimal value, when the variables x and y are the constraints described by the linear inequalities. This optimal value must come at a corner point of the feasible region.
Theorem 2
Let R be the feasible region for a linear programming problem and let z = ax + by be its objective function. If S is bounded, then z has both maximum and a minimum optimization value on R and every value comes at a corner point of JR.
Solved Example of Theorem 2Example: Suppose we have the following corner points (0, 0), (70, 0), (40, 30), and (0, 50). Then, substituting the above coordinate point in the equation of objective function z = 40x + 15y, we get For (0, 0) we get Z = 0 For (70, 0), we get Z = 2800 For (40, 30), we get Z = 2050 For (0, 50), we get Z = 750 Henceforth, the maximum value of Z appears at (70, 0) and the minimum value appears at (0, 0). This is the required solution of the linear programming problem. |
Read More:
| Chapter Related Concepts | ||
|---|---|---|
| Point Slope Form Formula | Collinear Points | Cartesian Coordinate System |
| Linear Functions | Horizontal and Vertical Lines | |
Methods to Solve Linear Programming Problems
[Click Here for Sample Questions]
There are two most important methods of solving linear programming problems which are as follows:
Linear Programming Corner Point Method
The corner point method tells that if a maximum or minimum value exists for a problem, then it determines the corner point of the feasible region.
Corner Point Method
Steps to Apply Corner Point Method
To apply the corner point method the below-mentioned steps must be applied:
- Find the feasible region of the linear programming problem.
- Find its corner points by solving the formed two equations of the lines intersecting at that point.
- Determine the objective function z = ax + by at each point.
- Let M and m to denote the largest and the smallest values of those points.
- If the feasible region is bounded, then M and m are the maximum and minimum values of the objective function at corner points.
- If two corner points of the feasible region are of the identical type, i.e. both produce the identical maximum or minimum value, then any point which is on the line segment joining these two points is also an optimal solution of the identical type.
Solved Example of Linear Programming Corner Point MethodExample: The problem is to maximize the profit function z = 40x + 15y with respect to the constraints x + 2y less than or equal to 100 x + 2y less than or equal to 70 x greater than or equal to 0, y Solution Step-1: We can find that the above equation has x greater than or equal to 0, and y greater than or equal to 0. Hence, we need to focus only on the first quadrant. Solution Step-2: First, we will try to plot the equation x + 2y = 100 from the given coordinate points (0, 50) and (100, 0). Then, let's plot the equation x + y = 70 using the coordinate point (70, 0) and (0, 70).
Linear Programming Graph 1 Plotting the two equations produced the above mentioned graph. Now, we need to identify the feasible region of the graph which is nothing but the common region determined through all the given constraints. So, the feasible region is shown in the below graph
Linear Programming Graph 2 |
Read More: Calculus Formula
Graphical Method
If the problem contains two decision variables, the best way to find the optimum solution is to use a graphical method. The set of inequalities is subjected to constraints in this manner.
- The inequalities are then plotted on an XY plane.
- Once all of the inequalities have been shown on the XY graph.
- The intersecting region will assist in determining the feasible region.
- The feasible area will not only give the best solution but also explain what values our model can take.
Steps to apply Graphical Method
-
Formulate the Linear programming problem.
First, we must identify the decision variables and determine the objective function to be maximized or reduced, which is described as a linear function of decision variables. Then, regarding the decision variables, identify the set of constraint conditions and describe them as linear inequalities or equations.
- Construct a graph and plot the constraint lines.
The graph must have 'n' dimensions, with 'n' being the number of decision variables. This should give you a sense of how complicated this phase will get as the number of decision variables increases.
- Determine the valid side of each constraint line.
This is used to identify the available space's domain. A primary way is to insert the origin (0,0) coordinates into the problem and see if the objective function has a physical solution or not. If yes, the valid side of the constraint lines is the one on which the origin is located. Otherwise, it's on the other side.
- Identify the feasible solution region.
On the graph, the feasible solution region is the one that is satisfied by all of the constraints. It might also be considered as the intersection of each constraint line's valid regions. A suitable solution for our objective function might be found at any point in this area.
- Plot the objective function on the graph.
Since we're working with linear equations, it'll obviously be a straight line. To avoid confusion, it must be drawn differently from the constraint lines. Choose the constant value in the objective function's equation at random to make it easily identifiable.
- Find the optimum point.
An optimal point is always found at one of the feasible region corners. Make sure this rule is oriented correctly in space. We need to know the direction of the objective function in a straight line. Begin sliding the graph towards the origin, starting from the far corner.
(A) Find the point of contact of the ruler with the feasible region which is closest to the origin if the purpose is to minimize the objective function.
(B) This is the optimal function minimization point.
Find the point of contact of the ruler with the feasible region that is the farthest from the origin if the purpose is to maximize the objective function. This is the most efficient way to maximize the function.
- Calculate the coordinates of the optimum point.
You'll need to find the coordinates of the optimum point once you've found it. Drawing two perpendicular lines from the point onto the coordinate axes and noting down the coordinates is a simple way to achieve this. To determine the optimized objective function, plug the values of these parameters into the objective function's equation.
Read More:
| Class 12 Maths Topics | ||
|---|---|---|
| Perpendicular Line Formula | Discriminant of an Equation | Coincident Lines |
| Distance between Two Points | Pair of Linear equation in two variables formula | Real Numbers Formula |
Applications of Linear Programming
[Click Here for Sample Questions]
Some real-world applications of linear programming are as follows:
Engineering Sector
Many engineering industries in the world use the concept of linear programming to solve design and manufacturing problems. It will provide maximum output for a given set of conditions.
Manufacturing Sector
Many manufacturing industries use the functions of linear programming to maximise the profit of the company and reduce the manufacturing cost of the product.
Energy Sector
The energy sector uses the formula of linear programming to increase the output and efficiency of production.
Transportation Sector
The transportation sector uses the function of linear programming to determine the transportation cost and increase the efficiency.
Read More: Angle between Two Planes
Things to Remember
- Linear programming is used to increase the output value and decrease the input value of a function.
- The non-negative restriction used in programming includes x ≥ 0 and y ≥ 0.
- The constraints applied to a linear programming problem include cx + dy ≤ e, fx + gy ≤ h.
- It will optimise the output by making certain assumptions.
- The method is used when multiple conditions are applied to solve a problem.
Read More: Linear Equations Applications
Sample Questions
Ques. There are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, the farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs Rs 10 per kg and ‘B’ costs Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that the nutrient requirements are met at a minimum cost? (5 marks)
Ans. Let the requirement of fertilizer 'A' be 'x' kg and that of B be 'y' kg.
Given that
The farmer requires at least 12kg of Nitrogen & 12kg of phosphoric acid for his crops.
The equation thus formed based on problem is
(12100)x+(4100)y ≥ 12
⇒12x+4y≥1200
⇒3x+y≥300 …(1)
Also (5100)x+(5100)y≥12
⇒5x+5y≥1200
⇒x+y≥240 ...(2)
Given that x≥0;y≥0 ...(3)
Total cost of fertiliser z=10x+8y
Solving the LPP
3x+y=300
x+y=240
x=0
y=0

The minimum value of z is obtained at C(30,210)
∴ Requirement of 'A' is 30kg & 'B' is 210kg.
Ques. A company manufactures three kinds of calculators: A, B and C in its two factories I and II. The company has got an order for manufacturing atleast 6400 calculators of kinds A, 4000 of kind B and 4800 of kind C. e daily output of factory I is of 50 calculators of kind A, 50 calculators of kind B and 30 calculators of kind C. e Daily output of factory II is of 40 calculators of kind A, 20 of kind B and 40 of kind C. e cost per day to run factory I is Rs 12,000 and of factory II is Rs 15,000. How many days do the two factories have to be in operation to produce the order with the minimum cost? Formulate this problem as an LPP and solve it graphically? (5 marks)
Ans. Let factories I and II be operated for x and y number of days respectively. Then the problem can be formulated as in L.P.P. as:
Minimise Z=12000x+15000y
Subject to constraints
50x+40y≥6400
⇒5x+4y≥640
50x+20y≥4000
⇒5x+2y≥400
30x+40y≥4800
⇒3x+4y≥480
x≥0,y≥0
We draw the lines 5x+4y≥640,5x+2y≥400,3x+4y≥480 and obtain the feasible region (unbounded and convex) shown shaded in the adjoining figure. the corner points are A(0,200),B(32,120),C(80,60) and D(160,0).
The values of Z at these points are 3000000, 2184000, 1860000 and 1920000 respectively. As the feasible region is unbounded, we draw the graph of the half plane.
12000x+15000y<1860000
i.e.,
12x+15y<1860
As there is no point common with the feasible region, therefore the minimum and minimum value of Z is Rs. 1860000.
It occurs at the point (80,60) i.e., Factory I should be operated for 80 days and factory II should be operated for 60 days to minimise the cost.

| Running Cost per day (in Rs) | A | B | C | |
|---|---|---|---|---|
| 12000 | I | 50 | 50 | 30 |
| 15000 | II | 40 | 20 | 40 |
Ques. A manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs 24 per package on nuts and Rs 18 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 10 hours a day. Make an LPP from above and solve it graphically? (5 marks)
Ans. Let x and y be nut packages produced each day, respectively.
Given that LLP is Maximize Z = 24x + 18y
From the problem:
2x+3y10
3x+2y10
x,y0

Now the vertices we get are
A(0,103), B(2,2) and C(103,0)
| Points | Z= 24x+18y |
|---|---|
| A(0,103) | Z= 0+60= Rs 60 |
| B(2,2) | Z= 40+36= Rs 84 (Max.) |
| C(103,0) | Z= 80+0= Rs 80 |
Hence 2 nuts & 2 bolts are needed to be produced to get max. Profit of Rs 84.
Ques. One kind of cake requires 200 g of flour and 25 g of fat, another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat, assuming that there is no shortage of the other ingredients used in making the cakes. Make it an LPP and solve it graphically? (5 marks)
Ans. Let number of first kind of cake be x and another kind of cake be y
So, total flour required =200x+100y g
and total fat required =25x+50y g
Since, maximum flour available is 5kg=5000g
∴200x+100y≤5000
⇒2x+y≤50…(1)
Also, maximum fat available is 1kg=1000g
∴25x+50y≤1000
⇒x+2y≤40...(2)
Since, the quantity of cakes can't be negative.
∴x≥0,y≥0...(3)
To find the maximum number of cakes that can be made.
Objective function is Z=x+y
After plotting graph by equation (1), (2) and (3), we got the feasible region

| Corner points | Value of Z=x+y |
|---|---|
| A (0,20) | 20 |
| B (20,10) | 30 (Maximum) |
| C (25,0) | 25 |
So, the maximum cakes that can be made are 30 and the first kind of cake will be 20 and second kind of cake will be 10.
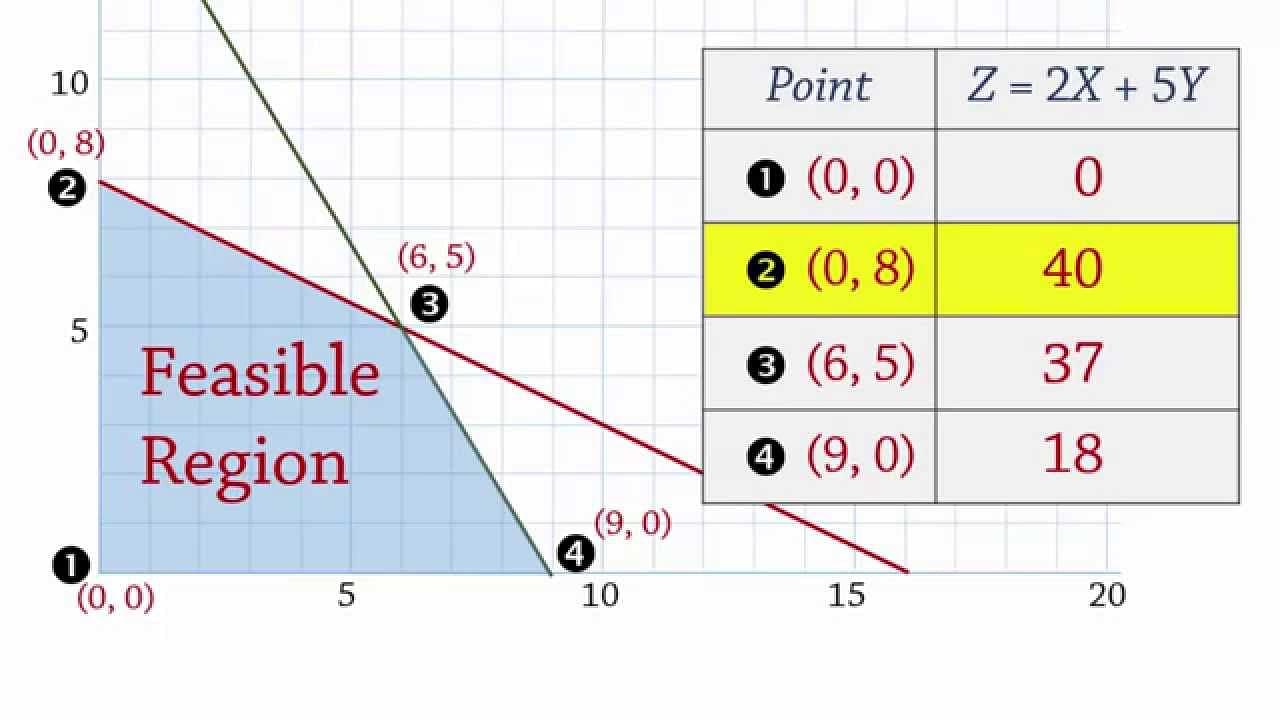
Ques. Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below: 2x+ 4y≤8, 3x + y≤6, x + y≤4; x≥0, y≥0 ? (4 marks)
Ans. Given that z=2x+5y,
Given constraints are
2x+4y≤8
⇒x+2y≤4 …(1)
3x+y≤6…(2)
x+y≤4…(3)
x≥0,y≥0.
To get the graph we have to draw the lines x+2y=4, 3x+y=6 and x+y=4 through [(4,0),(0,2)], [(2,0),(0,6)] and [(4,0),(0,4)] respectively.

With these inequalities we get the shaded region.
By solving Eq (1) and (2)
we get
x=58 and y=56
We can see that the feasible region OABC is a convex polygon with corner points-
O(0,0), A(2,0), B(58,56), C(0,2)
The solution we get at corner points.At O(0,0), z=2(0)+5(0)=0
At A(2,0), z=2(2)+5(0)=4
At B(58,56), z=2(58)+5(56)=546
At C(0,2), z=2(0)+5(2)=10
Therefore, z has maximum value at C =10.
Ques. A housewife wishes to mix together two kinds of food, X and Y, in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg of food is given below:

One kg of food X costs Rs 6 and one kg of food Y costs Rs 10. Formulate the above problem as a linear programming problem and find the least cost of the mixture which will produce the diet graphically. What value will you like to attach with this problem? (5 marks)
Ans. Let x kg of food X and y kg of food Y are mixed
And z represents the cost function.
Min z=6x+10y
According to LPP,
x+2y≥10
2x+2y≥12
⇒x+y≥6
3x+y≥8
By solving these inequalities we get (1,5) and (2,4)

At (1,5), z=6+50=56
At (2,4), z=12+40=52
Hence, when 2 kg of food X and 4 kg of food Y are mixed the mixture of least cost will be produced.
Ques. A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours of fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30 respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get a maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week? (5 marks)
Ans. Let the pieces of type A manufactured per week be x and the pieces of type B manufactured per week be y.
∴ max profit z=80x+120y
For A
Fabricating hours needed is 9 and finishing hours is 1
For B
Fabricating hours needed is 12 and finishing hours is 3
Maximum number of fabricating hours is 180.
∴9x+12y≤180
⇒3x+4y≤60
Max number of finishing hours is 30.
∴x+3y≤30
So the LPP will be formulated as
Max z=80x+120y subjected to the constraints, 3x+4y≤60, x+3y≤30, x≥0, y≥0
By solving these constraints we get
x=12,y=6
With this we get the area of feasible region as

Now we can see that the points bounded by the feasible region are A(0,10),B(12,6),C(20,0)
So the maximum profit will be
At A(0,10),z=80(0)+120(10)=1200
At B(12,6),z=80(12)+120(6)=1680
At C(20,0),z=80(20)+120(0)=1600
Hence, we can say that at C (12,6) we get maximum profit.
Therefore 12 pieces of type A and 6 pieces of type B should be manufactured per week to get a maximum profit of Rs.1680
Ques. A factory owner purchases two types of machine A and B for his factory. The requirements and the limitations for the machines are as follows,

He has a maximum area of 9000 m2 available and 72 skilled labours who can operate both the machines. How many machines of each type should he buy to maximize the daily output? (5 marks)
Ans. Let x machines of type A and y machines of type B be bought and let z be the daily output.
⇒ z=60x+40y …(1)
Maximum area available = 9000 m2
⇒1000x+1200y≤9000
5x+6y≤45 …(2)
Maximum labour available = 72 men
⇒12x+8y≤72
3x+2y<18 …(3)
Now, the mathematical formulation of given L.P.P. is
z=60x+40y
Subject to constraints (2) and (3)
5x+6y≤45
3x+2y≤18
Given that- x≥0,y≥0
We draw the line
5x+6y=45 and 3x+2y=18
Now we can observe a feasible region with corner points,
O(0,0), A(6,0), B(94,458) and C (0, 152)
At each corner point the value of z will be
At O(0,0): z=0
At A(6,0) :z= 360(max)
At B(94,458) :z= 360(max)
At C (0, 152) :z= 300
Hence, either 6 machines of type A and no machine of type B or 2 machines of type A and 6 machines of type B be used to have maximum output.
Ques. A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximise the profit? It is being given that at least one of each must be produced? (4 marks)
Ans. Let the number of necklaces produced be x and bracelets be y.
The inequality representing the number constraint is given as
x + y ≤ 24
Also the inequality representing the hour constraint is given as
x +12y ≤ 16
⇒(when multiplying the inequality by 2 we get )
2x + y ≤ 32
Also the non negative constraints
x≥0, y≥0
Let z be the total maximum profit.
Hence the equation can be given as
∴z = 100x + 300y, which is to be maximised
subject to the constraints,
x + y ≤ 24
2x + y ≤ 32
x, y ≥ 0
Ques. In order to supplement your daily diet, a person wishes to take some X and some wishes Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligram per tablet) are given as below:

The person needs at least 18 milligram of iron, 21 milligram of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is Rs 2 and Re 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost? (5 marks)
Ans. Let a person takes
x units of tablet X and y unit of tablet Y.
So, from the given information, we have
6x+2y ≥ 18
⇒3x+y ≥ 9…(1)
3x+3y ≥ 1
⇒x+y ≥ 7…(2)
And
2x+4y ≥ 16
⇒x+2y ≥ 8…(3)
Also, we know that here,
x≥ 0,y ≥ 0…(4)
The price of each tablet of X is Rs 2 and tablet Y is Rs 1
So, the corresponding LPP is minimise z= 2x + y subject to
3x+y≥ 9,x+y≥ 7x,x+y≥ 7,
x+2y≥ 8,x≥ 0,y≥ 0
From the graph, we get coordinates of corner points A, B, C and D as
A=(8,0)
B=(6,1)
C=(1,6)
D=(0,9)
[On solving x+2y=8 and x+y=7 we get, x=6 and y=1 and on solving 3x+y=9 and x+y=7,
we get x=1 and y=6]

| Corner Points | Values of z = 2x + y |
|---|---|
| (8, 0) | 16 |
| (6, 1) | 13 |
| (1, 6) | 8 (minimum) |
| (0, 9) | 9 |
Now we get 8 as the minimum value of Z at the corner point (1, 6). Since the region is unbounded. Therefore, it may be possible that 8 is not the minimum value of Z. So to check that we have
2x+y<8 …(5)
From the graph it is clear that it has no common point.
Therefore, z = 2x + y has 8 as minimum value
Hence, we can say that the person should take 1 unit of X tablet and 6 units of Y tablets for the given requirements with minimum cost of Rs 8.
Ques. A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped each day? (5 marks)
Ans. How many of each type should be created daily to maximize net earnings if each scientific calculator sold generates a $2 loss but each graphing calculator generates a $5 profit?
x: number of scientific calculators produced
y: number of graphing calculators produced
Because they can't make calculators with negative values,we have two constraints: x > 0 and y > 0. But in this case, we can ignore these limits because x > 100 and y > 80 are already present. Maximums are also given in the exercise: x 200 and y 170. x + y > 200 is the minimum shipping requirement; in other words, y > –x + 200. Our optimization equation for the profit relation will be P = –2x + 5y. As a result, the overall system is:
P = –2x + 5y, the equation when exposed to constraints, we get:
100 < x < 200
80 < y < 170
y > –x + 200
Ques. You'll have to get some filing cabinets. Cabinet X costs $10 per unit, takes up six square feet of floor space, and holds eight cubic feet of files, as you already know. Cabinet Y costs $20 per unit and holds twelve cubic feet of files. It takes up eight square feet of floor space. You have been allocated $140 to spend on this transaction, albeit you are not required to do so. Cabinets can only take up 72 square feet in the office. In order to optimize storage volume, how many of each model should you purchase? (4 marks)
Ans. The question asks how many cabinets I need to buy, thus these are the variables we'll use:
x: number of model X cabinets purchased
y: number of model Y cabinets purchased
Naturally, x and y are both greater than zero. Costs and floor space (each unit's "footprint") must be considered while optimizing storage capacity, therefore costs and floor space will be our restrictions, and volume will be our optimization equation.
cost: 10x + 20y < 140, or y < –( 1/2 )x + 7
space: 6x + 8y < 72, or y < –( 3/4 )x + 9
volume: V = 8x + 12y
If you buy eight of model X and three of model Y and test the corner points at (8, 3), (0, 7), and (12, 0), you should get a maximum volume of 100 cubic feet.
Also check:











Comments