
Collegedunia Team Content Curator
Content Curator
The inflection point, also known as the point of inflection, is the point where the function is neither concave nor convex. A function is a specific relation between two sets (input set and output set). Each member of the output set is linked to one or more members of the input set in a unique way. The function is denoted by the letter (f). Functions are classified into various types. Depending upon the nature of the graph, the function can be divided into two types namely;
- Convex Function
- Concave Function
Concavity and convexity can occur once or several times in a function. Thus, we can say,
- The function is concave upward when the second derivative is positive.
- The function is concave downward when the second derivative is negative.
A point where the second derivative disappears yet does not change the sign is also often called a point of undulation or undulation point.
Read More: NCERT Solutions For Class 12 Mathematics Chapter 10 Differential Equation
| Table of Content |
Key Terms: Inflection Point, Maxima, Minima, Concavity, Continuity, Differentiation, Integration, Slope, Convex Function, Concave Function
What is an Inflection Point?
[Click Here for Sample Questions]
Inflection point is a point where the concavity of a function does not change. It means that the function shifts from concave up to concave down, or vice versa. In other terms, an inflection point is defined as the point at which the rate of slope switches from increasing to decreasing or vice versa. These are usually stable points rather than local maxima or minima.

Inflection Point Meaning Infograph
Concavity of a Function
When the curve of a function bends down, it forms a concave shape. It is called the concavity of a function. The inflection point graphs show two forms of concavity:
- Concave Up: If a curve opens upward or bends up to form a cup-like shape, it is said to be concave up.
- Concave Down: If a curve opens downward or bends down to form a cup-like shape, it is said to be concave down. Tangent is beneath the curve if the slope of the tangent grows as the independent variable increases.
Read Also:
| Concept-Related Topics | ||
|---|---|---|
| Applications of Derivatives | Increasing and Decreasing Functions | Approximations |
Inflection Point Calculus
[Click Here for Previous Year Questions]
If f(x) is a differentiable function, then f(x) is:
- Concave up a point x = a, if f “(x) > 0 at a
- Concave down at a point x = a, if f “(x) < 0 at ‘a’.
Here, f “(x) is the second order derivative of the function f(x).
Solved Examples Related to Inflection PointQues: Is an inflection point a turning point? Ans: An inflection point may or may not be a turning point. This is because all the turning points are stationary, but not all stationary points can be defined as turning points. The point where the derivative of a function is zero, but its sign of derivative does not vary, can be identified as a point of inflection or saddle point. Ques: Find the inflection point for 2x3 + 2. Ans: As per the given question, we already are aware that 2x3 + 2. ⇒ \({d^2(2x^3+2) \over dx} = 0\) ⇒ 12x = 0 ⇒ x = 0 |
Read More:
| Related Topics | ||
|---|---|---|
| Differential Equation | Difference Between Relation and Function | First Order Differential Equation |
Inflection Point Graph
[Click Here for Sample Questions]
The slope of a graph of a function with a zero point is defined by the point of inflection. The function has an inflection point, as seen in the graph below.
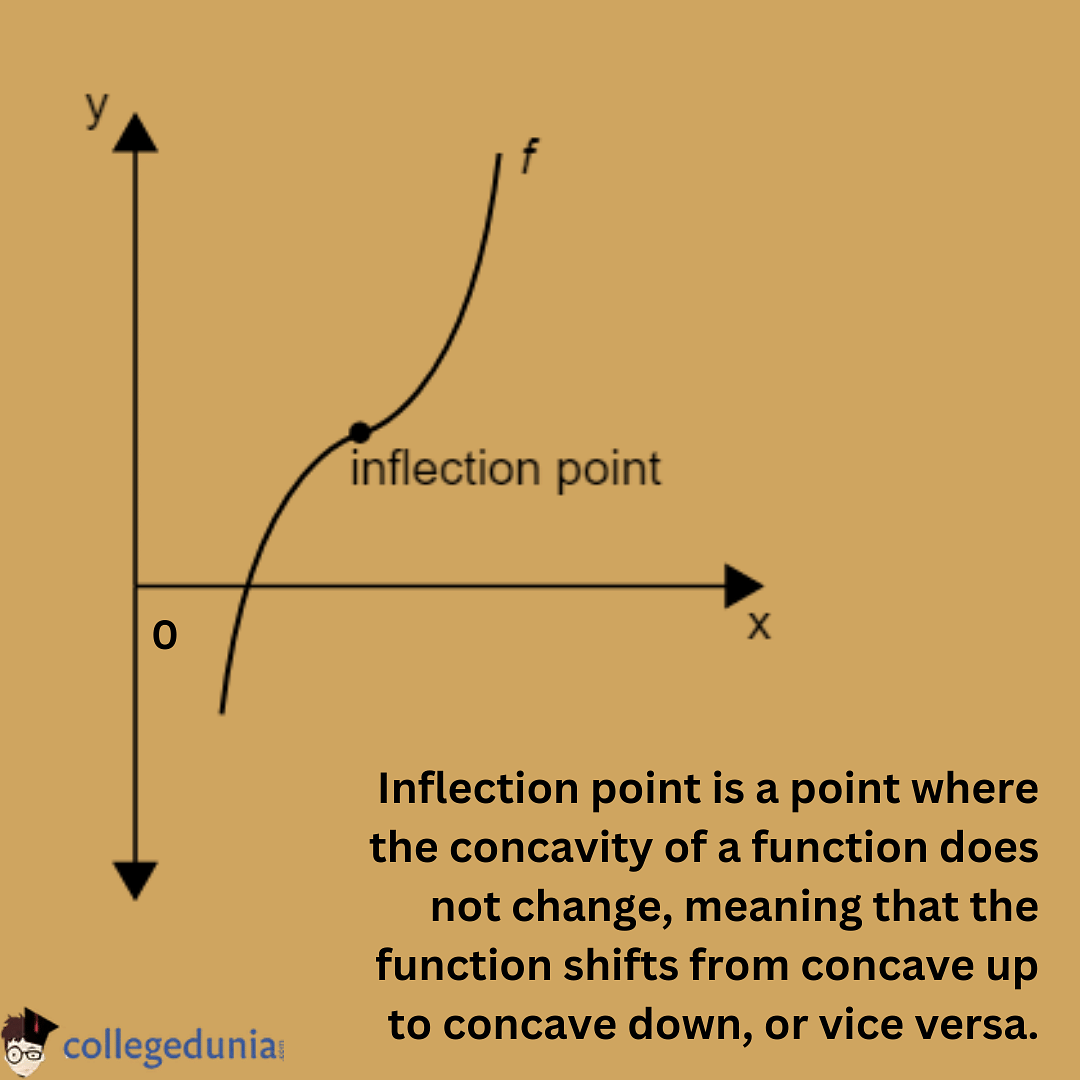
Point of Inflection
There might be more than one point of inflection in a single curve or within the prescribed interval of a function.
Finding Inflection Point on a Graph
A point on the curve where the concavity changes is called an inflection point i.e. a shift in the curvature sign. We know that the function is concave up if f " > 0, and concave down if f " 0. The point of inflection on a graph is when the function flips from positive to negative, or from negative to positive, at a given point x = c.
The sign of the second derivative of a function can be used to determine the inflection point of a function. The point of inflection can also be classified into two sorts based on the value of the function's first-order derivative, as shown below:
- The point is a stationary point of inflection if f'(x) equals zero.
- The point is a non-stationary point of inflection if f'(x) is not equal to zero.
Inflection Point of a Function
The Inflection point of a Function can be identified on the basis of the second derivative’s sign of the given function. By taking the value of the function’s first-order derivative, the point inflection can be further classified into two types:
- If f'(x) is equal to zero, the point is then a stationary point of inflection.
- If f'(x) is not equal to zero, the point is then a non-stationary point of inflection.
Read Also:
Things to Remember
- If the sign of f ′(x) does not change as x climbs through c, then c is neither a local maximum nor a local minimum. In fact, this type of point is known as a point of inflection.
- To find the inflection of a point, differentiate the function f(z), to get f(z). Solve the equation f(z) = 0 to get the values of z at minima or maxima or point of inflection.
- For each z value, find the values of f(z) a smaller and a little larger than z value. Determine whether you have a maximum or minimum point of inflection and then calculate the values of a function at the z value for the point of inflection.
- If the inflection point of the graph y = f(x) is at x = z, then the second derivative of f evaluated at z is 0. But the point of inflection is not determined if the second derivative of a function is 0 at a point.
Check More: Differential Equations Applications
Previous Year Questions
- Which of the following is divisible by … [AP EAPCET]
- If x>0 … [BITSAT 2018]
- If the function f(x) defined by … [KCET 2014]
- Solution of the differential equation cosxdy=y(sinx−y)dx,0<x<π2 is...[AIEEE 2010]
- If y(t) is a solution of (1+t)dy/dt − ty = 1 and y(0) = −1….[JEE Advanced 2003]
- The equation of the curve satisfying the differential equation ….[AMUEEE 2015]
- If xdy=y(dx+y/dy),y(1)=1 and y(x)>0. Then, y(−3) is equal to...[JEE Advanced 2005]
- Which of the following is a correct solution of xcosx(dy/dx)…..[AMUEEE 2014]
- Let f(x) be differentiable on the interval (0,∞) such that…...[AMUEEE 2014]
- If 8√x(√9+√x)dy=(√4+√9+√x)−1dx,x>0 and….[JEE Advanced 2017]
Sample Questions
Ques. Determine the inflection point for the given function f(x) = x2 – 24x2 + 11. (5 Marks)
Ans. Given function: f(x) = x4 – 24x2 + 11
The first derivative of the function is
f’(x) = 4x3 – 48x
The second derivative of the function is
f”(x) = 12x2 – 48
Set f”(x) = 0,
12x2 – 48 = 0
Divide by 12 on both sides, we get
x2 – 4 = 0
x2 = 4
Therefore, x = ± 2
To check or x = 2, substitute x = 1 and 3 in f”(x)
So, f”(1) = 12(1)2 – 48 = -36 (negative)
f”(3) = 12(3)2 – 48 = 276 (positive)
To check for x = -2, substitute x = 0 and -3 in f”(x)
So, f”(0) = 12(0)2 – 48 = -48 (negative)
f”(3) = 12(3)2 – 48 = 276 (positive)
Hence proved.
Now, substitute x = ± 2 in f”(x)
Therefore, it becomes
f”(2) = 12(2)2 – 48 = -69
f”(-2) = 12(-2)2 – 48 = -69
Therefore, the inflection points are (2, -69), and (-2, -69).
Ques. Find the point(s) of inflection for the function y = x3. (3 Marks)
Ans. A point of inflection is found where the graph (or image) of a function changes concavity. To find this algebraically, we want to find where the second derivative of the function changes sign, from negative to positive, or vice-versa. So, we find the second derivative of the given function y=x3.
The first derivative using the power rule
y = xn→y′ = nxn − 1 is,
y′ = 3x2 and the seconds derivative is y′′ = 6x.
We then find where this second derivative equals 0. 6x = 0 when x = 0.
We then look to see if the second derivative changes signs at this point. Both graphically and algebraically, we can see that the function y′′=6x does indeed change sign at, and only at, x = 0, so this is our inflection point.
Ques. Find all the points of inflection of: f(x)=−x3 + x2 − x + 1. (5 Marks)
Ans. In order to find the points of inflection, we need to find f′′(x) using the power rule, f(x) = xn → f′(x) = nxn − 1.
f(x) = −x3 + x2 − x + 1
f′(x) = −3x2 + 2x − 1
f′′(x) = −6x + 2
Now we set f′′(x) = 0, and solve for x.
−6x + 2=0
−6x = −2
x = 13
To verify this is a true inflection point we need to plug in a value that is less than it and a value that is greater than it into the second derivative. If there is a sign change around the point then it is a true inflection point.
Let x = 0
f′′(0) =−6 (0) + 2 = 2
Now let x = 1
f′′(1) = −6(1) + 2 = −4
Since the sign changes from a positive to a negative around the point x = 13, we can conclude it is an inflection point.
Ques. Find all the points of inflection of: f(t) = t5 − 3t3 + 2t + 100. (5 Marks)
Ans. In order to find the points of inflection, we need to find f′′(t) using the power rule f(x) = xn→f′(x) = nxn − 1.
f(t) = t5 −3t3 + 2t +100
f′(t) = 5t4 − 9t2 + 2
f′′(t) = 20t3 − 18t
Now lets factor f′′(t).
f′′(t) = t(20t2−18)
Now to find the points of inflection, we need to set f′′(t)=0.
t(20t2−18) = 0.
From this equation, we already know one of the point of inflection, t1=0.
To figure out the rest of the points of inflection we can use the quadratic equation.
Recall that the quadratic equation is
t= −b ± b2−4ac−−−−−−−√2a, where a,b,c refer to the coefficients of the equation
at2 + bt + c=0
In this case, a = 20, b = 0, c = -18.
t = −0 ± 02 − 4(20)(−18)−−−−−−−−−−−−−√(2)(20)
t = ±1440−−−−√40 = ±1210−−√40 = ±310−−√10
Thus the other 2 points of infection are:
t2 = 310−−√10
t3 = −310−−√10
To verify that they are all inflection points we need to plug in values higher and lower than each value and see if the sign changes.
Lets plug in x = −1, x = −12, x = 12, x = 1
f′′(−1) = 20(−1)3 − 18(−1) = −2
f′′(−12) = 20(−12)3 − 18(−12) = 6.5
f′′(12) = 20(12)3 − 18(12) = −6.5
f′′(1) = 20(1)3 − 18(1) = 2
Since there is a sign change at each point, all are points of inflection.
Ques. Find the points of inflection of f(x)=x2 − 2x + 1. (3 Marks)
Ans. In order to find the points of inflection, we need to find f′′(x)
f(x) = x2 − 2x + 1
f′(x) = 2x−2
f′′(x) = 2
Now we set f′′(x)=0.
0 = 2.
This last statement says that f′′(x) will never be 0. Thus there are no points of inflection.
Ques. Find the points of inflection of the following function: f(x) = x3 + 2x2 + x. (5 Marks)
Ans. The points of inflection of a given function are the values at which the second derivative of the function is equal to zero.
The first derivative of the function is:
f′(x) = 3x2 + 4x +1, and the derivative of this function (the second derivative of the original function), is
f′′(x) = 6x + 4.
Both derivatives were found using the power rule;
Solving 0 = 6x + 4, x = −23.
To verify that this point is a true inflection point we need to plug in a value that is less than the point and one that is greater than the point into the second derivative. If there is a sign change between the two numbers then the point in question is an inflection point.
Lets plug in x = −1,
6(−1) + 4 = −2.
Now plug in x = 0
6(0) + 4 = 4.
Therefore, x = −23 is the only point of inflection of the function.
Ques. Find all the points of inflection of: f(x) = x4 − x2 + 100. (3 Marks)
Ans. In order to find all the points of inflection, we first find f′′(x) using the power rule twice f(x) = xn → f′(x) = nxn − 1.
f(x) = x4 − x2 + 100
f′(x) = 4x3 − 2x
f′′(x) = 12x2 − 2
Now we set f′′(x)=0.
12x2 − 2 = 0
Thus the points of inflection are x = 1/√6 and x = −1/√6
Ques. Find the inflection point of this 3rd degree polynomial: 5x3 − 9x2 + 5x − 10. (3 Marks)
Ans. To find the inflection point we must find where the second derivative of a function is 0.
Calculating the second derivative is fairly simple. We just need to know that (xn)′=n⋅xn−1:
The first derivative is:
15x2 − 18x + 5
and if we take the derivative once more we get
30x − 18.
Setting this equal to zero, we get
30x − 18 = 0 → x = 18/30 = 3/5
And now all we have to do is plug this value, 3/5, into our original polynomial, to get the answer.
(3/5,−229/25)
Ques. Determine the point(s) of inflection for the function y = 3x5 − 10x4 + 10x3 + 7x + 1. (3 Marks)
Ans. Points of inflection occur when the second derivative changes signs.
y = 3x5 − 10x4 + 10x3 + 7x + 1
y′ = 15x4 − 40x3 + 30x2 + 7
y′′ = 60x3 − 120x2 + 60x = 60x (x2−2x+1) = 60x(x−1)2
The second derivative equals zero at x = 0 and x = 1. However, the factor (x−1) has degree two in the second derivative. This indicates that x=1 is a root of the second derivative with multiplicity two, so the second derivative does not change signs at this value. It only changes signs at x = 0. Since f(0) = 1, the point of inflection is (0,1).
Ques. Where does the function f(x)=5x3 + 53x2 + 11 have a point of inflection? (2 Marks)
Ans. The point of inflection of an object can be found by setting the second derivative of the function equal to zero and solving.
f′(x) = 15x2 + 10/3x.
f′′(x) = 30x + 10/3 = 0.
30x = −10/3, x = −1/9.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments