
Content Strategy Manager
Coplanar Lines are determined as the number of lines on the same plane. Coplanar Lines are a popular concept in 3D Geometry. If two or more lines lie on the same plane, they are said to be coplanar and the lines that do not lie in the same plane are called non-coplanar lines. In Geometry, Collinear and coplanar are two terms that often sound similar and confusing. the terms used to describe them. In each of these terms, "co" means "together," "linear" means "along a line," and "planar" points "on a plane." Thus, collinear indicates that they are parallel on a line, whereas coplanar implies that they are similar on a plane.
| Table of Contents |
Key Terms: Coplanar Lines, Three Dimensional Geometry, Non-Coplanar Lines, Vectors, Coplanar Points, Plane, Rectangular Prism, Lines
Read More: Coplanar Vector
What are Coplanar Lines?
[Click Here for Sample Questions]
Two or more lines are coplanar if they share the same space and plane. All of the polygon lines are coplanar concerning each other. If two or more lines lie on the same plane, they are coplanar, whereas lines that do not lay on the same plane are termed non-coplanar lines.
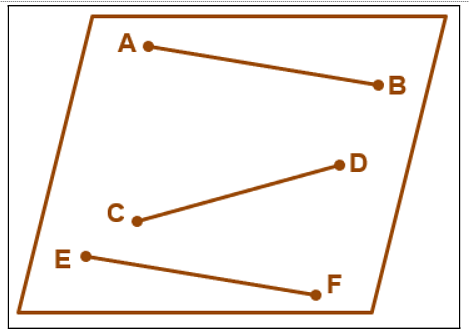
Coplanar Lines
Now. let us understand how to identify coplanar lines. Consider the rectangular prism shown below.

Rectangular Prism
Coplanar Lines in Geometry
The coplanar Lines in the above rectangular prism are:
- GF and CB are present on the right-side face of the prism (meaning they are lying on the same plane).
- CD and AB are present on the bottom face of the prism (meaning they are lying on the same plane).
- DH and AD are present on the left side of the prism (meaning they are lying on the same plane).
Non-Coplanar Lines in Geometry
The following lines are some non-coplanar lines in the above rectangular prism as they don't lie on the same plane, i.e., they don't lie on the same rectangle.
- HG and DA are not present on the same plane in the given diagram.
- BA and GC are not present on the same plane in the given diagram.
- HE and CB are not present on the same plane in the given diagram.
Thus, all these lines are non-coplanar.
Also Read:
| Related Articles | ||
|---|---|---|
| Scalar Triple Product of Vectors | Angle Between a Line and a Plane | Area of kite formula |
| Volume of Sphere | Differential Equations Applications | Circles |
Coplanarity in Theory
[Click Here for Sample Questions]
Coplanar lines are a frequently discussed issue in 3D Geometry. Coplanarity is defined in mathematical theory as the situation in which a certain number of lines are on the same plane; therefore, they are called coplanar. To recap, a plane is a two-dimensional shape that extends into infinity in three-dimensional space, whereas straight lines are represented by vector formulas (known as lines).
Read More: Edges, Faces, and Vertices
How to Determine Whether Given Two Lines are Coplanar?
[Click Here for Sample Questions]
If two lines are present in the same plane, then the two lines are said to be coplanar. Given below are the conditions for two lines to be coplanar both in vector form and cartesian form.
-
Condition for Coplanarity in Vector Form
r1 = 11 + λm1
r2 = 12 + λm2
Let us assume these two straight lines in the vector form as follows:
These equations signify that the very first line crosses through a point, let's call it L, whose position vector is provided by l1, and it is known to be lying parallel to m1. Likewise, the second line is said to cross through another point whose position vector is provided by l2 and parallel to m2.
Coplanarity requires that the line connecting the two points be perpendicular to the product of the two vectors, m1 and m2. The vector form of the line connecting the two locations is (l2 – l1). So far, we have:
(l2 –l1) . (m1 x m2) = 0
-
Condition for Coplanarity in Cartesian Form
The vector form is used to derive the requirement for coplanarity in the Cartesian form. Consider two locations in the Cartesian plane, L (x1, y1, z1) and M (x2, y2, z2). Consider two vectors, m1 and m2. Their corresponding direction ratios are denoted by a1, b1, c1 and a2, b2, c2.
The vector equation of the line connecting L and M is as follows:
LM = (x2 – x1)i + (y2 – y1)j + (z2 – z1)k
m1 = a1i + b1j + c1k
m2 = a2i + b2j + c2k
We will now utilise the vector mentioned above to generate our Cartesian condition. This may be used for computation purposes as is. According to the criteria mentioned earlier, the two lines are coplanar if LM. (m1 x m2) = 0. As a result, the matrix encoding this equation in Cartesian form is 0.
Read More: Coordinate Geometry
Real-World Examples of Coplanar Lines
[Click Here for Sample Questions]
- The grids may be found on graph paper. Because the grid's vertical and horizontal lines are both on the same sheet of paper, they are coplanar points.
- The hands-on watches and clocks are also coplanar. The second, minute and hour hands are all located in the same circular area.
- The lines of a notepad are parallel to one another. They are on the same plane because they are on the same page.
- These lines are not only coplanar but also parallel.

Real-Life Example of Coplanar Lines
Read More: Equation of a Plane in Three-Dimensional Space
Things to Remember
- If two lines are present in the same plane, then the two lines are said to be coplanar.
- Coplanarity is defined in mathematics as the situation in which a certain number of lines are on the same plane; therefore, they are called coplanar.
- Coplanarity exists between any two locations.
- There are many real-world examples of coplanar lines such as grids on graph paper, lines of a notepad, etc.
Also Read:
| Related Articles | ||
|---|---|---|
| Areas Related To Circles Formula | Area of Segment of a Circle | Difference Between Cube and Cuboid |
| Difference between Area and Volume | Relations and Functions | Formula Of Perimeter |
Sample Questions
Ques. Evaluate whether the lines (x + 3)/3 = (y – 1)/1 = (z – 5)/5 and (x + 1)/ -1 = (y – 2)/2 = (z – 5)/5 coplanar or not? (3 Marks)
Ans. Let us compare these point values with the general form of the equation of coplanarity.
(x1, y1, z1) = (-3, 1, 5)
(x2, y2, z2) = (-1, 2, 5).
Carefully see that,
a1, b1, c1 = -3, 1, 5
a2, b2, c2 = -1, 2, 5.
Using the cartesian form, solve the point of equations in a matrix form by calculating their determinant.
= 2(5 – 10) – 1(-15 + 5) + 0(-6 + 1) = -10 + 10 = 0
The determinant of the matrix or the solution of the equation of coplanarity is 0. Hence, we can easily claim that the given lines (x + 3)/3 = (y – 1)/1 = (z – 5)/5 and (x + 1)/ -1 = (y – 2)/2 = (z – 5)/5 are coplanar.
Ques. Explain the meaning of the term coplanar. Is it possible to state that collinear points are coplanar? (3 Marks)
Ans. Three or more points in the same plane are called coplanar points. A coplanar set is any set of three points in space. A group of four points might be coplanar or noncoplanar. Collinear points are ones whose occurrences occur along the same line. Coplanar points are those that are all located in the same plane. In the case of collinear points, a person can select one of an endless number of planes that include the line on which these points reside. As a result, they can be described as coplanar.
Ques. How does one establish that two vectors are coplanar? (3 Marks)
Ans. Two vectors can be proven to be coplanar if they satisfy the following conditions:
If the scalar triple product of any three vectors is zero.
If any three vectors are linearly dependent, n vectors will be coplanar if there are no more than two linearly independent vectors among them.
Ques. Show that lines x+3 / −3 = y–2 / 4 = z–5 / 5 and x+1 / −3 = y–2 / 3 = z+5 / 6 are coplanar. (5 Marks)
Ans. Let us compare these point values with the general form of the equation of coplanarity.
x1 = -3, y1 = 2, z1 = 5,
x2 = -1 , y2 = 2, z2 = -5,
Carefully see that,
a1 = -3 , b1 = 4, c1 = 5,
a2 = -3 , b2 = 3, c2 = 6
Using the cartesian form, solve the point of equations in a matrix form by calculating their determinant.
\(\begin{bmatrix}x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\[0.3em] a_1 & b_1 & c_1 \\[0.3em] a_2 & b_2 & c_2 \\[0.3em] \end{bmatrix}\)
\(\begin{bmatrix}2 & 0 &-10 \\[0.3em] -3 & 4 & 5 \\[0.3em] -3 & 3 & 6 \\[0.3em] \end{bmatrix}\)
= – 12
The determinant of the matrix or the solution of the equation of coplanarity is 12. Hence, we can easily claim that the given lines x+3 / −3 = y–2 / 4 = z–5 / 5 and x+1 / −3 = y–2 / 3 = z+5 / 6 are not coplanar.
Ques. Evaluate the determinant and find whether the given points A = (0, 1, -1), B = (4, 3, 1) and C = (3, 2, 1) can be called coplanar or not. (5 Marks)
Ans. The points given in the question are A = (0, 1, -1), B = (4, 3, 1) and C = (3, 2, 1)
To test their coplanarity, we need to obtain the scalar product of the three given vectors.
\([\overrightarrow{A}, \overrightarrow{B}, \overrightarrow{C}] = \overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\)To find the cross product of B x C, we need to make a matrix and then find its determinant. The determinant will be the result of the cross product of B and C.
\(\overrightarrow{B} \times \overrightarrow{C} = \begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\[0.3em]4 & 3 & 1 \\[0.3em]3 & 2 & 1 \\[0.3em] \end{bmatrix} \)\(\overrightarrow{B} \times \overrightarrow{C} \) = \(\overrightarrow{i}\)\(\begin{bmatrix}3 & 1 \\[0.3em]2 & 1 \\[0.3em] \end{bmatrix} \) – \(\overrightarrow{j}\)\(\begin{bmatrix}4 & 1 \\[0.3em]3 & 1 \\[0.3em] \end{bmatrix} \) + \(\overrightarrow{k}\)\(\begin{bmatrix}4 & 3 \\[0.3em]3 & 2 \\[0.3em] \end{bmatrix} \)
= 1\(\overrightarrow{i}\) – 1\(\overrightarrow{j}\) – 1\(\overrightarrow{k}\)
Now, calculate the dot product of a with B x C.
\(\overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\) = (0,1,-1).(1,-1,-1) = 0 – 1+1 = 0
Since the dot product of all the three vectors is 0, we can say that the given vectors are coplanar.
Ques. Show that the given points A = (2, 3, 5), B = (4, 1, 6), C = (1,8, 4), and D = (1, 6, 4) are not coplanar. (5 Marks)
Ans. In order to find the coplanarity of these four points, we need to find the vectors AB, AC, AD
\(\overrightarrow{AB}\)= (4 - 2, 1 - 3, 6 - 5) = (2, -2, 1) \(\overrightarrow{AC}\)= (1 - 2, 8 - 3, 4 - 5) = (-1, 5, -1) \(\overrightarrow{AD}\)= (1 - 2, 6 - 3, 4 - 5) = (-1, 3, -1)Now, formulate these points into a matrix and then find its determinant. The determinant will be the result will be the cross product of the three calculated vectors.
= \(\begin{bmatrix}2 & -2 & 1 \\[0.3em]-1 & 5 & -1 \\[0.3em]-1 & 3 & -1 \\[0.3em] \end{bmatrix} \)
= 2 . \(\begin{bmatrix}5 & -1 \\[0.3em]3 & -1 \\[0.3em] \end{bmatrix} \) – 2 . \(\begin{bmatrix}-1 & -1 \\[0.3em]-1 & -1 \\[0.3em] \end{bmatrix} \) + 1 \(\begin{bmatrix}-1 & 5 \\[0.3em]-1 & 3 \\[0.3em] \end{bmatrix} \)
= – 2
Since the dot product of all the three vectors is not equal to 0, we can say that the given vectors are not coplanar.
Ques. Evaluate the determinant and find whether the given points A = (5, 2, 3), B = (1, 6, 7) and C = (4, 2, 5) can be called coplanar or not. (5 Marks)
Ans. The points given in the question are A = (5, 2, 3), B = (1, 6, 7) and C = (4, 2, 5)
To test their coplanarity, we need to obtain the scalar product of the three given vectors.
\([\overrightarrow{A}, \overrightarrow{B}, \overrightarrow{C}] = \overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\)To find the cross product of B x C, we need to make a matrix and then find its determinant. The determinant will be the result of the cross product of B and C.
\(\overrightarrow{B} \times \overrightarrow{C} = \begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\[0.3em]1 & 6 & 7 \\[0.3em]4 & 2 & 5 \\[0.3em] \end{bmatrix} \)\(\overrightarrow{B} \times \overrightarrow{C} = \overrightarrow{i} \) . \(\begin{bmatrix}6 &7 \\[0.3em]2 &5 \\[0.3em] \end{bmatrix} \) – \(\overrightarrow{j}\) . \(\begin{bmatrix}1 &7 \\[0.3em]4 &5 \\[0.3em] \end{bmatrix} \) + \(\overrightarrow{k}\) \(\begin{bmatrix}1 &6 \\[0.3em]4 &2 \\[0.3em] \end{bmatrix} \)
= 16 \(\overrightarrow{i} \) + 23 \(\overrightarrow{j} \) – 22\(\overrightarrow{k} \)
Now, calculate the dot product of a with B x C.
\(\overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\) = (5,2,3) . (16,23,-22) = 80 + 46 – 66 = 60
Since the dot product of all the three vectors is 60, we can say that the given vectors are not coplanar.
Ques. Evaluate the determinant and find whether the given points A = (5, 1, 1), B = (3, 3, 1) and C = (2, 2, 1) can be called coplanar or not. (5 Marks)
Ans. The points given in the question are A = (5, 2, 3), B = (1, 6, 7) and C = (4, 2, 5)
To test their coplanarity, we need to obtain the scalar product of the three given vectors.
\([\overrightarrow{A}, \overrightarrow{B}, \overrightarrow{C}] = \overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\)To find the cross product of B x C, we need to make a matrix and then find its determinant. The determinant will be the result of the cross product of B and C.
\(\overrightarrow{B} \times \overrightarrow{C} = \begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\[0.3em]3 & 3 & 1 \\[0.3em]2 & 2 & 1 \\[0.3em] \end{bmatrix} \) \(\overrightarrow{B} \times \overrightarrow{C} = \overrightarrow{i} \) . \(\begin{bmatrix}3 &1 \\[0.3em]2 &1 \\[0.3em] \end{bmatrix} \) – \(\overrightarrow{j} \) \(\begin{bmatrix}3 &1 \\[0.3em]2 &1 \\[0.3em] \end{bmatrix} \) + \(\overrightarrow{k} \) \(\begin{bmatrix}3 &3 \\[0.3em]2 &2 \\[0.3em] \end{bmatrix} \)Now, calculate the dot product of a with B x C.
\(\overrightarrow{A} . (\overrightarrow{B} \times \overrightarrow{C})\) = (5,2,3) . (16,23,-22) = 80 + 46 – 66 = 60Since the dot product of all the three vectors is 60, we can say that the given vectors are not coplanar.
Ques. Show that the given points A = A = (1, 5, 7), B = (6, 3, 1), C = (2 ,9, 5), and D = (7, 6, 5) are not coplanar. (5 Marks)
Ans. In order to find the coplanarity of these four points, we need to find the vectors AB, AC, AD
\(\overrightarrow{AB}\)= (6 - 1, 3 - 5, 1 - 7) = (5, -2, -6) \(\overrightarrow{AC}\)= (2 - 1, 9 - 5, 5 - 7) = (-1, 4, -2) \(\overrightarrow{AD}\)= (7 - 2, 6 - 5, 5 - 7) = (6, 1, -2)Now, formulate these points into a matrix and then find its determinant. The determinant will be the result of the cross product of the three calculated vectors.
= \(\begin{bmatrix}5 & -2 & -6 \\[0.3em]-1 & 4 & -2 \\[0.3em]6 & 1 & -2 \\[0.3em] \end{bmatrix} \)
= 5 . \(\begin{bmatrix}4 & -2 \\[0.3em]1 & -2 \\[0.3em] \end{bmatrix} \) – (-2) . \(\begin{bmatrix}-1 & -2 \\[0.3em]6 & -2 \\[0.3em] \end{bmatrix} \) – 6 \(\begin{bmatrix}-1 & 4 \\[0.3em]6 & 1 \\[0.3em] \end{bmatrix} \)
= 148
Since the dot product of all the three vectors is not equal to 0, we can say that the given vectors are not coplanar.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments