JEE Main 2025 April 4 Physics Question Paper is available for download. NTA conducted JEE Main 2025 Shift 1 B.Tech Exam on 4 April 2025 from 9:00 AM to 12:00 PM and for JEE Main 2025 B.Tech Shift 2 appearing candidates from 3:00 PM to 6:00 PM. The JEE Main 2025 3rd April B.Tech Question Paper was Moderate to Tough.
Also Check: JEE Main 2025 Question Paper with Solution PDF Download
JEE Main 2025 April 4 Shift 1 Physics Question Paper with Solutions
| JEE Main 2025 April 4 Shift 1 Physics Question Paper Pdf | Download PDF | View Solution |

JEE Main 2025 Physics Questions with Solutions
Question 1:
The mean free path and the average speed of oxygen molecules at 300 K and 1 atm are \(3 \times 10^{-7} \mathrm{~m}\) and \(600 \mathrm{~m} / \mathrm{s}\), respectively. Find the frequency of its collisions.
View Solution
1. Given:
- Mean free path, \(\lambda = 3 \times 10^{-7} \mathrm{~m}\)
- Average speed, \(v_{avg} = 600 \mathrm{~m/s}\)
2. Frequency of collisions:
\[ Frequency = \frac{v_{avg}}{\lambda} = \frac{600}{3 \times 10^{-7}} = 2 \times 10^{9} \mathrm{~s^{-1}} \]
Therefore, the correct answer is (3) \(2 \times 10^{9} / \mathrm{s}\). Quick Tip: The frequency of collisions is given by the average speed divided by the mean free path.
A small mirror of mass \(m\) is suspended by a massless thread of length \(l\). Then the small angle through which the thread will be deflected when a short pulse of laser of energy \(E\) falls normal on the mirror ( \(c=\) speed of light in vacuum and \(g=\) acceleration due to gravity).
View Solution
1. Force due to the laser beam:
\[ F = \frac{2P}{c} = \frac{2}{c} \frac{dE}{dt} \]
2. Change in momentum of the mirror:
\[ m(V - 0) = \int F dt = \frac{2}{c} \int dE = \frac{2E}{c} \]
3. Using work-energy theorem:
\[ W_g = \Delta K \]
\[ -\frac{mg l (1 - \cos \theta)}{l} = \frac{1}{2} m V^2 \]
\[ \frac{g l (1 - \cos \theta)}{l} = \frac{1}{2} \left( \frac{4E^2}{m^2 c^2} \right) \]
\[ \frac{g l \theta^2}{2} = \frac{2E^2}{m^2 c^2} \]
\[ \theta = \frac{2E}{mc \sqrt{gl}} \]
Therefore, the correct answer is (4) \(\theta=\frac{2 \mathrm{E}}{\mathrm{mc} \sqrt{\mathrm{gl}}}\). Quick Tip: Use the work-energy theorem to find the deflection angle.
Two liquids A and B have \(\theta_{\mathrm{A}}\) and \(\theta_{\mathrm{B}}\) as contact angles in a capillary tube. If \(K=\cos \theta_{\mathrm{A}} / \cos \theta_{\mathrm{B}}\), then identify the correct statement:
View Solution
1. Given:
\[ K = \frac{\cos \theta_{\mathrm{A}}}{\cos \theta_{\mathrm{B}}} \]
2. Interpretation:
- If \(K\) is negative, \(\cos \theta_{\mathrm{A}}\) and \(\cos \theta_{\mathrm{B}}\) are of opposite signs.
- This implies that one liquid has a concave meniscus and the other has a convex meniscus.
Therefore, the correct answer is (3) K is negative, then liquid A has concave meniscus and liquid B has convex meniscus. Quick Tip: The sign of \(K\) indicates the nature of the meniscus of the liquids.
Which of the following are correct expression for torque acting on a body?
A. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{L}}\)
B. \(\ddot{\tau}=\frac{\mathrm{d}}{\mathrm{dt}}(\ddot{\mathrm{r}} \times \ddot{\mathrm{p}})\)
C. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \frac{\mathrm{d} \dot{\mathrm{p}}}{\mathrm{dt}}\)
D. \(\ddot{\tau}=\mathrm{I} \dot{\alpha}\)
E. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{F}}\)
( \(\ddot{r}=\) position vector; \(\dot{\mathrm{p}}=\) linear momentum; \(\ddot{\mathrm{L}}=\) angular momentum; \(\ddot{\alpha}=\) angular acceleration; \(\mathrm{I}=\) moment of inertia; \(\ddot{\mathrm{F}}=\) force; \(\mathrm{t}=\) time \()\)
Choose the correct answer from the options given below:
View Solution
1. Correct expressions for torque:
- B. \(\ddot{\tau}=\frac{\mathrm{d}}{\mathrm{dt}}(\ddot{\mathrm{r}} \times \ddot{\mathrm{p}})\)
- C. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \frac{\mathrm{d} \dot{\mathrm{p}}}{\mathrm{dt}}\)
- D. \(\ddot{\tau}=\mathrm{I} \dot{\alpha}\)
- E. \(\ddot{\tau}=\ddot{\mathrm{r}} \times \ddot{\mathrm{F}}\)
Therefore, the correct answer is (3) B, C, D and E Only. Quick Tip: Torque can be expressed in terms of position vector, linear momentum, angular momentum, and force.
In a Young's double slit experiment, the slits are separated by 0.2 mm. If the slits separation is increased to 0.4 mm, the percentage change of the fringe width is:
View Solution
1. Fringe width formula:
\[ \beta = \frac{D \lambda}{d} \]
2. Percentage change of fringe width:
- If \(d\) is doubled, \(\beta\) is halved.
- Therefore, the percentage change is \(50%\).
Therefore, the correct answer is (3) \(50 %\). Quick Tip: The fringe width is inversely proportional to the slit separation.
An alternating current is represented by the equation, \(\mathrm{i}=100 \sqrt{2} \sin (100 \pi \mathrm{t})\) ampere. The RMS value of current and the frequency of the given alternating current are
View Solution
1. RMS value of current:
\[ i_{rms} = \frac{i_0}{\sqrt{2}} = 100 \mathrm{~A} \]
2. Frequency of the current:
\[ f = \frac{\omega}{2\pi} = \frac{100\pi}{2\pi} = 50 \mathrm{~Hz} \]
Therefore, the correct answer is (3) \(100 \mathrm{~A}, 50 \mathrm{~Hz}\). Quick Tip: The RMS value of an alternating current is given by the peak value divided by \(\sqrt{2}\).
Consider the sound wave travelling in ideal gases of \(\mathrm{He}, \mathrm{CH}_{4}\), and \(\mathrm{CO}_{2}\). All the gases have the same ratio \(\frac{\mathrm{P}}{\rho}\), where P is the pressure and \(\rho\) is the density. The ratio of the speed of sound through the gases \(\mathrm{v}_{\mathrm{He}}: \mathrm{v}_{\mathrm{CH}_{4}}: \mathrm{v}_{\mathrm{CO}_{2}}\) is given by
View Solution
1. Speed of sound formula:
\[ v_{sound} = \sqrt{\frac{\gamma P}{\rho}} \]
2. Ratio of specific heats (\(\gamma\)):
- \(\gamma_{\mathrm{He}} = \frac{5}{3}\)
- \(\gamma_{\mathrm{CH}_{4}} \approx \frac{4}{3}\)
- \(\gamma_{\mathrm{CO}_{2}} \approx \frac{4}{3}\)
3. Ratio of speeds of sound:
\[ \sqrt{\frac{5}{3}}: \sqrt{\frac{4}{3}}: \sqrt{\frac{4}{3}} \]
Therefore, the correct answer is (3) \(\sqrt{\frac{5}{3}}: \sqrt{\frac{4}{3}}: \sqrt{\frac{4}{3}}\). Quick Tip: The speed of sound in a gas depends on the ratio of specific heats (\(\gamma\)).
In an electromagnetic system, the quantity representing the ratio of electric flux and magnetic flux has dimension of \(\mathrm{M}^{\mathrm{B}} \mathrm{L}^{\mathrm{O}} \mathrm{T}^{\mathrm{B}} \mathrm{A}^{\mathrm{S}}\), where value of 'Q' and 'R' are
View Solution
1. Dimensions of electric flux (\(\phi_E\)) and magnetic flux (\(\phi_M\)):
\[ \phi_E = EA \quad and \quad \phi_M = BA \]
2. Ratio of electric flux to magnetic flux:
\[ \frac{\phi_E}{\phi_M} = \frac{E}{B} \]
3. Dimensions of \(\frac{E}{B}\):
\[ \left[ \frac{E}{B} \right] = \frac{[E]}{[B]} = \frac{MLT^{-2}A^{-1}}{MT^{-2}A^{-1}} = LT^{-1} \]
4. Dimensions of \(\frac{E}{B}\):
\[ \left[ \frac{E}{B} \right] = LT^{-1} \]
Therefore, the correct answer is (4) \((1,-1)\). Quick Tip: The ratio of electric flux to magnetic flux has dimensions of \(LT^{-1}\).
When an object is placed 40 cm away from a spherical mirror an image of magnification \(\frac{1}{2}\) is produced. To obtain an image with magnification of \(\frac{1}{3}\), the object is to be moved:
View Solution
1. Given:
- Object distance, \(u = -40 \mathrm{~cm}\)
- Magnification, \(m = \frac{1}{2}\)
2. Magnification formula:
\[ m = \frac{f}{f - u} \]
\[ \frac{1}{2} = \frac{f}{f - (-40)} \]
\[ f + 40 = 2f \implies f = 40 \mathrm{~cm} \]
3. For magnification \(\frac{1}{3}\):
\[ \frac{1}{3} = \frac{40}{40 - u} \]
\[ 40 - u = 120 \implies u = -80 \mathrm{~cm} \]
Therefore, the correct answer is (1) 40 cm away from the mirror. Quick Tip: Use the magnification formula to find the object distance.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R. Assertion A: In photoelectric effect, on increasing the intensity of incident light the stopping potential increases. Reason R: Increase in intensity of light increases the rate of photoelectrons emitted, provided the frequency of incident light is greater than threshold frequency.
View Solution
1. Assertion A:
- The stopping potential does not depend on the intensity of light.
- Therefore, Assertion A is false.
2. Reason R:
- Increasing the intensity of light increases the rate of photoelectrons emitted.
- Therefore, Reason R is true.
Therefore, the correct answer is (2) \(\mathbf{A}\) is false but \(\mathbf{R}\) is true. Quick Tip: The stopping potential in the photoelectric effect does not depend on the intensity of light.
If \(\overrightarrow{\mathrm{L}}\) and \(\overrightarrow{\mathrm{P}}\) represent the angular momentum and linear momentum respectively of a particle of mass ' \(m\) ' having position vector \(\overrightarrow{\mathrm{r}}=\mathrm{a}(\hat{\mathrm{i}} \cos \omega \mathrm{t}+\hat{\mathrm{j}} \sin \omega \mathrm{t})\). The direction of force is
View Solution
1. Position vector:
\[ \overrightarrow{\mathrm{r}} = \mathrm{a}(\hat{\mathrm{i}} \cos \omega \mathrm{t} + \hat{\mathrm{j}} \sin \omega \mathrm{t}) \]
2. Acceleration:
\[ \overrightarrow{\mathrm{a}} = -\omega^2 \overrightarrow{\mathrm{r}} \]
3. Force:
\[ \overrightarrow{\mathrm{F}} = m \overrightarrow{\mathrm{a}} = -m \omega^2 \overrightarrow{\mathrm{r}} \]
Therefore, the direction of force is opposite to the direction of \(\overrightarrow{\mathrm{r}}\). Quick Tip: The force is proportional to the acceleration, which is opposite to the position vector in this case.
A body of mass \(m\) is suspended by two strings making angles \(\theta_{1}\) and \(\theta_{2}\) with the horizontal ceiling with tensions \(\mathrm{T}_{1}\) and \(\mathrm{T}_{2}\) simultaneously. \(\mathrm{T}_{1}\) and \(\mathrm{T}_{2}\) are related by \(\mathrm{T}_{1}=\sqrt{3} \mathrm{~T}_{2}\). the angles \(\theta_{1}\) and \(\theta_{2}\) are
View Solution
1. Given:
\[ \mathrm{T}_{1} \sin \theta_{1} + \mathrm{T}_{2} \sin \theta_{2} = \mathrm{mg} \]
\[ \mathrm{T}_{1} = \sqrt{3} \mathrm{~T}_{2} \]
2. Substitute \(\mathrm{T}_{1}\):
\[ \sqrt{3} \mathrm{~T}_{2} \sin \theta_{1} + \mathrm{T}_{2} \sin \theta_{2} = \mathrm{mg} \]
\[ \mathrm{T}_{2} (\sqrt{3} \sin \theta_{1} + \sin \theta_{2}) = \mathrm{mg} \]
3. For \(\theta_{1} = 60^{\circ}\) and \(\theta_{2} = 30^{\circ}\):
\[ \mathrm{T}_{2} (\sqrt{3} \cdot \frac{\sqrt{3}}{2} + \frac{1}{2}) = \mathrm{mg} \]
\[ \mathrm{T}_{2} = \frac{\mathrm{mg}}{2} \]
Therefore, the correct answer is (2) \(\theta_{1}=60^{\circ} \theta_{2}=30^{\circ}\) with \(\mathrm{T}_{2}=\frac{\mathrm{mg}}{2}\). Quick Tip: Use the equilibrium condition to find the tensions and angles.
Current passing through a wire as function of time is given as \(I(t)=0.02 \mathrm{t}+0.01 \mathrm{~A}\). The charge that will flow through the wire from \(t=1 \mathrm{~s}\) to \(\mathrm{t}=2 \mathrm{~s}\) is:
View Solution
1. Charge calculation:
\[ q = \int I(t) dt \]
\[ q = \int_{1}^{2} (0.02t + 0.01) dt \]
\[ q = \left[ 0.02 \frac{t^2}{2} + 0.01t \right]_{1}^{2} \]
\[ q = \left[ 0.01(4) + 0.01(2) \right] - \left[ 0.01(1) + 0.01(1) \right] \]
\[ q = 0.04 \mathrm{~C} \]
Therefore, the correct answer is (4) 0.04 C. Quick Tip: Integrate the current function to find the charge.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R. Assertion A: The kinetic energy needed to project a body of mass \(m\) from earth surface to infinity is \(\frac{1}{2} \mathrm{mgR}\), where R is the radius of earth. Reason R: The maximum potential energy of a body is zero when it is projected to infinity from earth surface.
View Solution
1. Assertion A:
- The kinetic energy needed to project a body of mass \(m\) from earth surface to infinity is \(\frac{1}{2} \mathrm{mgR}\).
- This is incorrect.
2. Reason R:
- The maximum potential energy of a body is zero when it is projected to infinity from earth surface.
- This is correct.
Therefore, the correct answer is (1) A False but \(\mathbf{R}\) is true. Quick Tip: The kinetic energy needed to project a body to infinity is equal to the potential energy at the earth's surface.
The Boolean expression \(\mathrm{Y}=\mathrm{A} \overline{\mathrm{B}} \mathrm{C}+\overline{\mathrm{AC}}\) can be realised with which of the following gate configurations.
A. One 3-input AND gate, 3 NOT gates and one 2-input OR gate, One 2-input AND gate
B. One 3-input AND gate, 1 NOT gate, One 2-input NOR gate and one 2-input OR gate
C. 3-input OR gate, 3 NOT gates and one 2-input AND gate
Choose the correct answer from the options given below:
View Solution
1. Boolean expression:
\[ Y = A \overline{B} C + \overline{AC} \]
2. Gate configurations:
- A. One 3-input AND gate, 3 NOT gates and one 2-input OR gate, One 2-input AND gate
- B. One 3-input AND gate, 1 NOT gate, One 2-input NOR gate and one 2-input OR gate
Therefore, the correct answer is (2) A,B Only. Quick Tip: Use the Boolean expression to determine the correct gate configurations.
In an experiment with a closed organ pipe, it is filled with water by \(\left(\frac{1}{5}\right)\) th of its volume. The frequency of the fundamental note will change by
View Solution
1. Initial frequency:
\[ f_1 = \frac{v}{4l} \]
2. Frequency with water:
\[ f_2 = \frac{v}{4(4l/5)} = \frac{5v}{16l} \]
3. Percentage change:
\[ \frac{\Delta f}{f} = \frac{\frac{5v}{16l} - \frac{v}{4l}}{\frac{v}{4l}} \times 100 = 25% \]
Therefore, the correct answer is (1) \(25 %\). Quick Tip: The frequency of the fundamental note changes with the length of the pipe.
Two simple pendulums having lengths \(l_{1}\) and \(l_{2}\) with negligible string mass undergo angular displacements \(\theta_{1}\) and \(\theta_{2}\), from their mean positions, respectively. If the angular accelerations of both pendulums are same, then which expression is correct?
View Solution
1. Angular acceleration:
\[ \alpha = -\omega^2 \theta \]
\[ \omega = \sqrt{\frac{g}{l}} \]
2. Equating angular accelerations:
\[ \frac{g}{l_1} \theta_1 = \frac{g}{l_2} \theta_2 \]
\[ \theta_1 l_2 = \theta_2 l_1 \]
Therefore, the correct answer is (4) \(\theta_{1} l_{2}=\theta_{2} l_{1}\). Quick Tip: The angular acceleration of a pendulum depends on its length and angular displacement.
Two infinite identical charged sheets and a charged spherical body of charge density ' \(\rho\) ' are arranged as shown in figure. Then the correct relation between the electrical fields at \(\mathrm{A}, \mathrm{B}, \mathrm{C}\) and D points is:
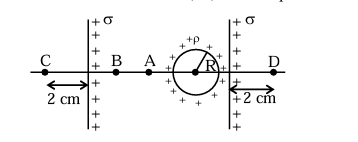
View Solution
1. Electric field at points A and B:
- \(\vec{E}_{A} > \vec{E}_{B}\)
2. Electric field at points C and D:
- \(\vec{E}_{C} \neq \vec{E}_{D}\)
Therefore, the correct answer is (3) \(\vec{E}_{C} \neq \vec{E}_{D} ; \vec{E}_{A}>\vec{E}_{B}\). Quick Tip: The electric field depends on the arrangement and charge density of the sheets and spherical body.
Two small spherical balls of mass 10 g each with charges \(-2 \mu \mathrm{C}\) and \(2 \mu \mathrm{C}\), are attached to two ends of very light rigid rod of length 20 cm. The arrangement is now placed near an infinite nonconducting charge sheet with uniform charge density of \(100 \mu \mathrm{C} / \mathrm{m}^{2}\) such that length of rod makes an angle of \(30^{\circ}\) with electric field generated by charge sheet. Net torque acting on the rod is:
View Solution
1. Electric field due to the charge sheet:
\[ E = \frac{\sigma}{2 \epsilon_0} \]
2. Torque acting on the rod:
\[ \tau = PE \sin \theta \]
\[ \tau = \left[ 2 \times 10^{-6} \times \frac{2}{10} \right] \left[ \frac{100 \times 10^{-6}}{2 \times 8.85 \times 10^{-12}} \right] \frac{1}{2} \]
\[ \tau = \frac{10}{8.85} = 1.12 \mathrm{~Nm} \]
Therefore, the correct answer is (2) 1.12 Nm. Quick Tip: The torque acting on a dipole in an electric field is given by the product of the dipole moment and the electric field.
Considering the Bohr model of hydrogen like atoms, the ratio of the radius \(5^{\text {th }}\) orbit of the electron in \(\mathrm{Li}^{2+}\) and \(\mathrm{He}^{+}\)is
View Solution
1. Radius of the \(5^{th}\) orbit for \(\mathrm{Li}^{2+}\):
\[ r_{5} = \frac{5^2}{3} a_0 \]
2. Radius of the \(5^{th}\) orbit for \(\mathrm{He}^{+}\):
\[ r_{5} = \frac{5^2}{2} a_0 \]
3. Ratio of the radii:
\[ \frac{r_{\mathrm{Li}^{2+}}}{r_{\mathrm{He}^{+}}} = \frac{2}{3} \]
Therefore, the correct answer is (4) \(\frac{2}{3}\). Quick Tip: The radius of an orbit in the Bohr model depends on the principal quantum number and the atomic number.
A circular ring and a solid sphere having same radius roll down on an inclined plane from rest without slipping. The ratio of their velocities when reached at the bottom of the plane is \(\sqrt{\frac{\mathrm{x}}{5}}\) where \(\mathrm{x}=\) _______.
View Solution
1. Mechanical energy conservation:
\[ K_i + U_i = K_f + U_f \]
\[ 0 + Mgh = \frac{1}{2} mv^2 \left(1 + \frac{k^2}{R^2}\right) + 0 \]
\[ v = \sqrt{\frac{2gh}{1 + \frac{k^2}{R^2}}} \]
2. Ratio of velocities:
\[ \frac{v_{ring}}{v_{solid sphere}} = \sqrt{\frac{1 + \frac{2}{5}}{1 + 1}} = \sqrt{\frac{7}{10}} \]
\[ x = 3.5 \approx 4 \]
Therefore, the correct answer is (4) 4. Quick Tip: Use mechanical energy conservation to find the velocities of the ring and the solid sphere.
Two slabs with square cross section of different materials \((1,2)\) with equal sides \((l)\) and thickness \(\mathrm{d}_{1}\) and \(\mathrm{d}_{2}\) such that \(\mathrm{d}_{2}=2 \mathrm{~d}_{1}\) and \(l>\mathrm{d}_{2}\). Considering lower edges of these slabs are fixed to the floor, we apply equal shearing force on the narrow faces. The angle of deformation is \(\theta_{2}=2 \theta_{1}\). If the shear moduli of material 1 is \(4 \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}\), then shear moduli of material 2 is \(\mathrm{x} \times 10^{9} \mathrm{~N} / \mathrm{m}^{2}\), where value of x is _______ .
View Solution
1. Deformation angle:
\[ 2 \theta_{1} = \theta_{2} \]
\[ 2 \frac{\sigma_{1}}{\eta_{1}} = \frac{\sigma_{2}}{\eta_{2}} \]
\[ 2 \left( \frac{F}{l d_{1} \eta_{1}} \right) = \frac{F}{l d_{2} \eta_{2}} \]
\[ \eta_{2} = \frac{\eta_{1}}{4} = 1 \times 10^{9} \]
\[ x = 1 \]
Therefore, the correct answer is (1) 1. Quick Tip: Use the deformation angle to find the shear modulus of the material.
Distance between object and its image (magnified by \(-\frac{1}{3}\) ) is 30 cm. The focal length of the mirror used is \(\left(\frac{\mathrm{x}}{4}\right) \mathrm{cm}\), where magnitude of value of x is _______ .
View Solution
1. Given:
\[ m = -\frac{1}{3} \]
\[ -\frac{v}{u} = \frac{1}{3} \implies v = \frac{u}{3} \]
2. Distance between object and image:
\[ u - v = 30 \mathrm{~cm} \]
\[ u - \frac{u}{3} = 30 \implies u = 45 \mathrm{~cm}, \quad v = 15 \mathrm{~cm} \]
3. Focal length:
\[ \frac{1}{f} = \frac{1}{v} + \frac{1}{u} = \frac{1}{15} + \frac{1}{45} = \frac{4}{60} \]
\[ f = \frac{60}{4} = 15 \mathrm{~cm} \]
\[ x = 45 \]
Therefore, the correct answer is (45). Quick Tip: Use the magnification formula to find the object and image distances, then calculate the focal length.
Four capacitors each of capacitance \(16\,\mu F\) are connected as shown in the figure. The capacitance between points A and B is: \underline{\hspace{1cm (in \(\mu F\)).
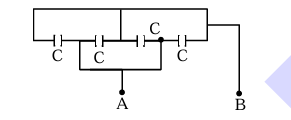
View Solution
1. Redraw the circuit:
- The capacitors are connected in parallel.
2. Equivalent capacitance:
\[ C_{eq} = 4C = 4 \times 16 \mu \mathrm{F} = 64 \mu \mathrm{F} \]
Therefore, the correct answer is (64) \(64 \mu \mathrm{F}\). Quick Tip: Use the parallel connection of capacitors to find the equivalent capacitance.
Conductor wire ABCDE with each arm 10 cm in length is placed in magnetic field of \(\frac{1}{\sqrt{2}}\) Tesla, perpendicular to its plane. When conductor is pulled towards right with constant velocity of \(10 \mathrm{~cm} / \mathrm{s}\), induced emf between points A and E is _______ mV.
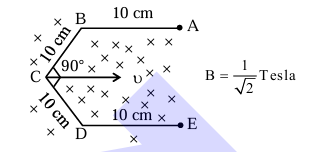
View Solution
1. Induced emf:
\[ \varepsilon = Bv \ell_{\mathrm{AB}} \]
\[ \varepsilon = \frac{1}{\sqrt{2}} \times \frac{10 \mathrm{~cm}}{s} \times 2 \left( 10 \sin 45^{\circ} \right) \mathrm{cm} \]
\[ \varepsilon = 10 \mathrm{~mV} \]
Therefore, the correct answer is (10) 10 mV. Quick Tip: Use Faraday's law to calculate the induced emf.
















Comments