
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Trapezoidal rule is used for approximating the definite integral using the numeric method. In this integration rule, the curve is divided into small trapezoids. Then, sum all the trapezoidal areas to get the total area of the curve. It is also known as the trapezoid or trapezium rule. The trapezoidal rule is based on Newton Cotes formula that says we can find the value of integral as nth border polynomial.
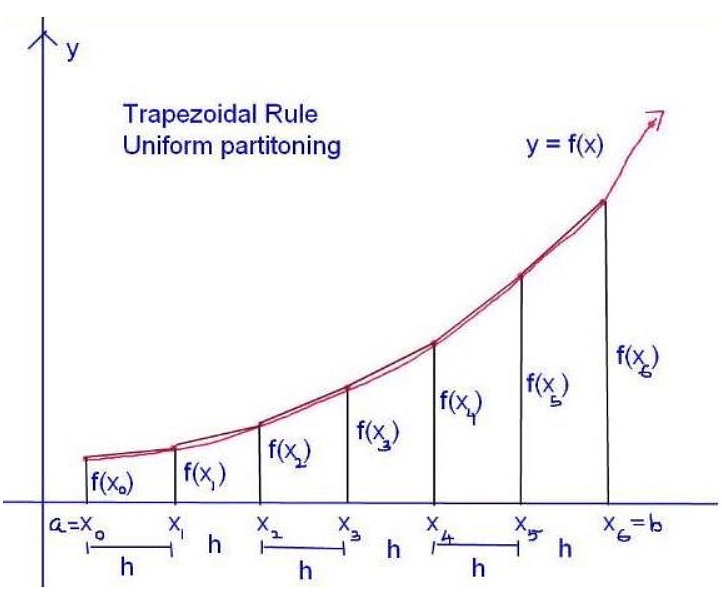
An Illustration of Trapezoidal Rule Uniform Partitioning
The trapezoidal rule determines the definite integral of type a∫b F(x)dx. The region under this curve is divided into multiple trapezoids and then the area is calculated. It is important to note that F(x) must be continuous between the intervals [a,b].
| Table of Content |
Key takeaways: Trapezoidal Rule, Definite Integral, Trapezoids, Area Under the Curve, Simpson’s Rule, Continous function, Integration rule, Integral
Trapezoidal Rule Formula
[Click Here for Sample Questions]
Consider F(x) as a continuous function in the interval [a,b]. According to the definition, divide this interval into n equal subintervals each of equal width.

Trapezoidal Rule
Δx = (b-a)/n
xi = [a, x0 , x1 , x2 , x3 , x4 ,..... , xn, b] (all possible values of x )
To approximate the area of the definite integral of a∫b f(x)dx, the trapezoidal rule is given by:
a∫b f(x) dx ≈ Tn = Δx/2[ f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)]
Where, xi = a + iΔx
Also, n→∞, R.H.S of the given expression approaches a∫b f(x)dx.
The video below explains this:
Trapezoid Formula Detailed Video Explanation:
Also Read:
Derivation of Trapezoidal Rule Formula
[Click Here for Sample Questions]
Let, f(x) be a continuous function in [a,b]. Consider the curve given in the below figure. Now, divide the curve into n trapezoids of equal width. Check the first trapezoid has length y0 or f(x0) and height Δx.

Derivation of Trapezoidal Rule Formula
Area of Trapezoid = 1/2 (Sum of length of parallel sides) x (perpendicular distance between the parallel sides)
= 1/2 (f(a) + f(b))(b-a)
Area of first trapezoids is given by, (1/2) Δx[f(x0) + f(x1)].
Area of second trapezoid is given by, (1/2) Δx[f(x1) + f(x2)]
Area of third trapezoid is given by, (1/2) Δx[f(x2) + f(x3)],
and so on.
Thus, by adding areas of all trapezoids, we get
a∫b f(x) dx ≈ (Δx/n)[f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)]
where, Δx = (b-a)/2 and n = number of subintervals.
How to Use Trapezoidal Rule?
[Click Here for Sample Questions]
The trapezoidal rule is used to calculate the definite integral of the function F(x). It determines the area under the region formed by dividing the curve into multiple trapezoids.
To calculate the area under the curve of the function f(x) using the trapezoidal rule follow the steps:
Step I: Write the number of subintervals (n) between “a” and “b”.
Step 2: Calculate the subinterval width, Δx = (b-a)/n.
Step 3: Calculate the values of f(x0), f(x1), f(x2)......f(xn).
Step 4: Put all these values in the trapezoidal rule formula:
a∫b f(x) dx ≈ Tn = Δx/2[ f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)]
Difference Between Trapezoidal and Simpson’s Rule
[Click Here for Sample Questions]
Both Trapezoidal and Simpson’s rule determine the definite integral of the function F(x). However, there are a few points that make these two rules different. The main differences are given below:
| Trapezoidal Rule | Simpson’s Rule |
|---|---|
| The boundary between the ordinates (a & b) is considered straight. | The boundary between the ordinates is considered as an arc of a parabola. |
| It can be applied to any number of ordinates. | There is a limitation in this rule, the number of ordinates should be odd. |
| Trapezoidal Rule is given by, a∫b f(x) dx ≈ (b-a/2n)[f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)] | Simpson’s Rule is given by, a∫b f(x) dx ≈ (b-a/3n)[f(x0) + 4f(x1) + 2f(x2) + 4f(x3) +....... 4f(xn-1) + f(xn)] |
Things to Remember
- The trapezoidal rule is used for estimating the definite integral.
- It calculates the total area under the curve by dividing the region into small trapezoids, calculating their area and adding them.
- Trapezoidal rule is based on Newton Cotes formula.
- The area of a particular region can be calculated by trapezoidal rule using the formula; a∫b f(x) dx ≈ (b-a/2n)[f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)]
Also Read:
Sample Questions
Ques. Find the area under the curve for the curve passing through the points (0,2), (0.5,4), (2,10), and (2.5,12) using the formula. (3 marks)
Ans. Write the given points in the tabular form we have,
| x | 0 | 0.5 | 1 | 1.5 |
| y | 2 | 4 | 10 | 12 |
Given that, y0 = 2
y1 = 4
y3 = 10
y4 = 12
Δx = (0.5 - 0) = (1 - 0.5) = (1.5 - 1) = 0.5
Using Trapezoidal Formula,
Area = Tn = Δx/2 [y0 + 2y1 + 2y2 +...... +2yn-1 + yn]
= 0.5/2 [2 + 2x4 + 2x10 + 12]
= 0.5/2 [42]
= 10.5
Therefore, the area under the curve is 10.5 sq units.
Ques. Find the area under the curve y=x2 between the x=0 and x=3 using the trapezoidal rule taking step size 2. (3 marks)
Ans. Given, y=x2
Δx = 2
Find values of y for different values of x using the equation y=x2
| x | 0 | 1 | 2 | 3 |
| y=x2 | y0=0 | y1=1 | y2=4 | y3=9 |
Using Trapezoidal Formula,
Area = Δx/2 [y0 + 2y1 + 2y2 + y3]
= 2/2 [0 + 2x1 + 2x4 + 9]
= 19
Therefore, the area under the curve is 19 sq. units
Ques. Use the Trapezoidal Rule to approximate 0∫4 x2dx with n=2. (3 marks)
Ans. Using the trapezoidal formula result we have,
a∫b f(x)dx = [f(a) + f(b)](b-a)/n
f(x) = x2
a = 0
b = 4
n = 2,
f(a=0) = 0
f(b=4) = 16
Δx = (4-0)/2 = 2
0∫4 x2dx = [16 + 0](4 - 2)/2
= 16
The approximate value is 16.
Ques. Use the trapezoidal rule to find 1∫4 √1+x dx with n = 9. (5 marks)
Ans. Given, f(x) = (1+x)1/2
Δx = (b-a)/n
= (4-1)/9
= 1/3
Now, divide the curve into 9 subintervals with the length Δx=1/3 the following 9 subintervals are,
a= 1, 4/3, 5/3, 2, 7/3, 8/3, 3, 10/3, 11/3, 4 = b
Now, calculate the values of functions with these endpoint,
f(x0) = f(1) = √2 = 1.41
f(x1) = f(4/3) = √7/3 = 0.88
f(x2) = f(5/3) = √8/3 = 0.94
f(x3) = f(2) = √3 = 1.73
f(x4) = f(7/3) = √10/3 = 1.05
f(x5) = f(8/3) = √11/3 = 1.10
f(x6) = f(3) = √4 = 2
f(x7) = (10/3) = √13/3 = 1.20
f(x8) = (11/3) = √14/3 = 1.24
f(x9) = (4) = √5 = 2.23
a∫b f(x)dx = Δx/2[f(x0) + 2f(x1) + 2f(x2) + 2f(x3) +....... 2f(xn-1) + f(xn)]
= 1/6 [1.41 + 2(0.88 + 0.94 + 1.73 + 1.05 + 1.10 + 2 + 1.20 + 1.24) + 2.23]
= 1/6 [14.98]
= 2.4966 ≈ 2.5
Hence, 1∫4 √1+x dx ≈ 2.4966
Ques. Approximate the integral 0∫2 (1 + cos[2√x])dx by using trapezoidal rule with n = 1, 2, and 4 subintervals. (5 marks)
Ans. Given, f(x) = (1 + cos[2√x])
f(0) = 2
f(1) = 1+ cos2
f(2) = 1+ cos2√2
f(3) = 1+ cos2√3
f(4) = 1+ cos4
For n=1,
T1 = [(2-0/1)]/2 [f(0) + f(2)]
= [2 + 1+cos2√2]
= [3 +cos2√2]
= [3 + 0.99]
= 3.99
For n=2,
T2 = [(2-0)/2]/2 [f(0) + 2f(1) + f(2)]
= 1/2 [2 + 2(1+cos2) + (1+cos2√2)]
= 1/2 [5 + 2cos2 + cos2√2]
= 1/2 [5+ 1.99 + 0.99]
= 3.99
For n=4,
T4 = [(2-0)/4]/2 [f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)]
= 1/4 [2 + 2(1+cos2) + 2(1+cos2√2 + 2(1+cos2√3) + (1+cos4)]
= 1/4 [9 + 2cos2 + 2cos2√2 + 2coss2√3 + cos4]
= 1/4 [9+ 1.99 + 1.99 + 1.99 + 0.99]
= 3.99
Ques. Use the Trapezoidal rule with n=8 to evaluate 0∫2 1/(1+x2)dx. Calculate the approximate value of π. (5 marks)
Ans. Using Trapezoidal formula we have,
T8 = Δx/2 [f(x0) + 2f(x1) + f(x2)+...... 2f(x7) + f(x8)]....(1)
f(x) = 1/(1+x2)
Δx = b-a/n = 2-0/8 = 1/4 = 0.25
Now, calculate f(xi) for different values of xi
(b = Δx + a )
x= a <xi <b = 0, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2
| x | 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.50 | 1.75 | 2 |
| f(x) | 1 | 0.94 | 0.8 | 0.64 | 0.5 | 0.39 | 0.30 | 0.25 | 0.2 |
Putting the values in equation 1 we have,
T8 = 0.25/2 [1 + 2(0.94+0.8+0.64+0.5+0.39+0.3+0.25) + 0.2]
= 0.125 [1.2 + 7.64]
= 0.125 x 8.84
= 1.105
Hence, 0∫2 1/(1+x2)dx = 1.105
Now, evaluate this integral
0∫2 1/(1+x2)dx = [arctanx]20 = arctan2 - arctan0 = 1.107 - 0 = 1.107(π/2.85)
Hence, the approximate value of π is given by;
π/2.85 ≈ 0∫2 1/(1+x2)dx
π ≈ 2.85 x 1.105
π ≈ 3.149
Ques. Calculate the approximate value of the area under the curve f(x) = 4x-x2 between x=0 and x=3 using trapezoidal rule with n = 4 subintervals. Also, calculate the % error of the approximation. (5 marks)
Ans. The Trapezoidal Rule with n = 4 is written as,
T4 = Δx/2 [f(x0) + 2f(x1) + 2f(x2) + 2f(x3) + f(x4)].....(1)
f(x) = 4x-x2
a= 0
b=3
n=4,
The width of subintervals is,
Δx = (b-a)/n = 3-0/4 = 3/4 = 0.75
xi = [a,b] = [0, 0.75, 1.5, 2.25, 3] (b= Δx + a)
Now, calculate the values of the function at different points xi
f(x0) = f(0) = 0
f(x1) = f(0.75) = 2.4375
f(x2) = f(1.5) = 2.75
f(x3) = f(2.25) = 3.9375
f(x4) = f(3) = 4
The approximate value of the area under the curve is,
T4 = 0.75/2 [0 + 2(2.4375+2.75+3.9375) + 4]
= 0.375 [4 + 22.25]
= 0.375 x 26.25
= 9.84 —--- (2)
The true solution can be found by integration
0∫3 (4x-x2)dx = [4x2/2 - x3/3]30 = 36/2 -27/3 = 9….(3)
The relative error is calculated by
|ε| = (9.84 - 9)/9.84 ≈ 0.085
Hence, a relative %error ≈ 8.53%
Ques. The curve y=ex2 is bonded by the x-axis, y-axis, and the line x=3 and forms a region R. (5 marks)
(a) Complete the table by calculating the value of y corresponding to x = 0.8 to x = 1.6

(b) Using a trapezoidal rule, calculate the approximate value for the region R using all the values of the above table.
Ans. a) We have,
f(x) = ex2
R = region formed between f(x), x-axis, y-axis, and the line x=2.
Completing the table, put the values
f(x2) = f(0.8) = e(0.8)2= e0.64
f(x4) = f(1.6) = e(1.6)2= e2.56
Hence the completed table is;
| x | 0 | 0.4 | 0.8 | 1.2 | 1.6 | 2 |
| y=f(x) | e0 | e0.16 | e0.64 | e1.44 | e2.56 | e4 |
b) Now, calculate the approximate value for the region R using all the values of the table is given by,
0∫2 ex2dx = Δx/2 [f(x0) + 2f(x1) + 2f(x3) + 2f(x4) + f(x5)].....(1)
Δx = (b-a)/n = (2-0)/5 = 0.4
f(x0) = f(0) = e0 = 1
f(x1) = f(0.4) = e0.16 = 1.173
f(x2) = f(0.8) = e0.64 = 1.896
f(x3) = f(1.2) = e1.44 = 4.22
f(x4) = f(1.6) = e2.56 = 12.93
f(x5) = f(2) = e4 = 54.60
Putting all these values in equation 1 we have,
0∫2 ex2 dx = 0.4/2 [1 + 2(1.173+1.896+4.22+12.93) + 54.60]
= 0.2 [55.60 + 33.14]
= 0.2 x 88.75
≈ 17.75
Hence, the approximate value of the area of Region R is 17.75
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments