
Jasmine Grover Content Strategy Manager
Content Strategy Manager
Differential calculus is the study of the definition, properties, and applications of a function's derivative. Derivative of a function is the primary object of study in differential calculus. The process of differentiation is the finding of the derivative.
Key terms: Differential calculus, Inverse Integration, Trigonometric Functions, Domain and Variable, Calculus, Differentiation, Rate of change, Curves, Integral calculus
Calculus
[Click Here for Sample Questions]
Calculus is a field of mathematics that studies rate of change and how it may be used to solve equations. It is based on the micro differences being added together. Following are the two branches of calculus.
- Differential Calculus - Differential calculus deals with the rate of changes and slopes of curves.
- Integral Calculus - Integral calculus deals with accumulation of quantities and the areas under and between curves.
However, the fundamental theorem of calculus binds these two types together.
Graph of Calculus
Basics of Differential Calculus
[Click Here for Sample Questions]
The derivative of a function is defined as the rate of change of functions with regard to specified values for every given value. Differentiation is the process of determining a function's derivative. Following are some of the key terms in differential calculus fundamentals:
Functions
A function is a relationship between a set of inputs and a set of outputs in which each input corresponds to one output exactly. "f(x)" is the symbol for the function.
Dependent Variable
A dependent variable is a variable whose value is always determined by the value of another variable known as an independent variable. The result variable is also known as the dependent variable. A dependent variable is a variable that is assessed from a mathematical expression utilising an independent variable.
Independent Variable
The inputs to the functions that specify the quantity being controlled in an experiment are known as independent variables. Consider the example of y=3x. Because the value of y is fully reliant on the value of x, x is known as the independent variable and y is known as the dependent variable.
Domain and Range
The input values of a function are simply defined as the domain, and the output value of a function is simply defined as the range. Take, for example, f(x) = 5x, where the domain values or input values are {1, 2, 3} and the range of a function is given as
f(1) = 5(1) = 5
f(2) = 5(2) = 10
f(3) = 5(3) = 15
Hence, the range of this function will be {5,10,15}.
Limits
In calculus, the limit is extremely significant. In calculus, limits are used to define continuity, integrals, and derivatives. A function's limit is defined as follows:
Let's imagine the function "f" is defined on an open interval containing certain numbers, such as "a," with the exception of "a" itself. The limit of a function f(x) is represented as:
limxa f(x) = L, if given >0,
>0 such that 0<x-a< implies f(x)=L<
meaning, limit f(x) as “x” approaches “a” is “L”.
Interval
A range of numbers exists between two given numbers, which is defined as an interval. There are two different sorts of intervals:
- Open interval: It is defined as the set of all real integers x that satisfy the condition a<x<b. It has the following representation: (a, b)
- Closed interval: It is defined as the set of all real integers x such that ax and an xb, or more succinctly, axb, and it is represented by (a, b).
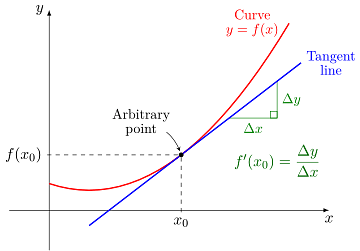
Derivatives
The derivative is the most basic tool in differential calculus. The derivative is a mathematical expression that depicts the pace of change. It aids in demonstrating the amount by which the function changes at a given location. A slope is the name for the derivative. It determines how steep a function's graph is. It is the ratio of a function's change in value to the change in the independent variable. dy/dx represents the derivative of y with respect to x.
Formulas
[Click Here for Sample Questions]
Let's say we have a function f(x), and the rate of change of that function with respect to x at a point 'o' in its domain may be stated as;
at point o, df(x)/dx
Alternatively, df/dx at o
If y = f(x) is a quantity, then f'(x) is the derivative of the function f. (x). Also, if x and y vary with respect to variable t, we can construct the derivative in the form of differential equations using the chain rule formula as follows:
f'(x)=dydx=dydtdxdt;dxdt0
| d(x)/dx | 1 |
| d(ax)/dx | a |
| d(xn)/dx | n xn-1 |
| d(cosx)/dx | -sin x |
| d(sinx)/dx | cos x |
| d(tanx)/dx | sec2 x |
| d(cotx)/dx | -cosec2 x |
| d(secx)/dx | sec x. tan x |
| d(cosec x)/dx | -cosec x. cot x |
| d(lnx)/dx | 1/x |
| d(ex)/dx | ex |
| d(ax)/dx | (ln a) ax |
| d(sin-1 x)/dx | 1/(1 - x2) |
| d(tan-1 x)/dx | 1/(1 + x2) |
| d(sec-1 x)/dx | 1/(x2 - 1) |
Important Topics for JEE MainAs per JEE Main 2024 Session 1, important topics included in the chapter differential calculus are as follows:
Some memory based important questions asked in JEE Main 2024 Session 1 include:
|
Things to Remember
- Differential calculus is used to find the rate of change of a quality with respect to others.
- While working with curves, finding the maximum and minimum value of a curve can be done by using differential calculus.
- Calculus plays a huge role in everyday life as well by calculating profit and loss of business using graphs, and change of the temperature.
- Many complex physics equations can be derived from differential calculus.
Also Read:
Sample Questions
Ques. Find the particular solution of the differential equation = 1 + x + y + xy, given that y = 0 when x = 1. All India 2014 (4 marks)
Ans. The differential equation is
dy/dx=1+x+y+xy
dy/dx=1(1+x)+y(1+x)
dy/dx=(1+x)+(1+y) ...(i)
On separating variables, we get
1(1+y)dy=(1+x)dx …(ii)
On integrating both sides of Eq. (ii), we get
1(1+y)dy=(1+x)dx
log1+y=x+x22+C ...(iii)
Also, given that y = 0, when x = 1.
On substituting x = 1, y = 0 in Eq. (iii), we get
log 1+0=1+12+CC=-32 (because, log1=0)
Now, on substituting the value of C in Eq. (iii), we get
log1+y=x+x^2-32
Above is the required particular solution of the given differential equation.
Ques. Form the differential equation for the circle family with a y-axis centre and a radius of 3 units. (4 marks)
Ans. The general equation of the family of circles having a centre on the y-axis is
x2 + (y – b)2 = r2
Given the radius of the circle is 3 units.
The differential equation of the family of circles having a centre on the y-axis and radius 3 units is as below:
x2 + (y – b)2 = 32
x2 + (y – b)2 = 9 ……(i)
Differentiating (i) with respect to x,
2x + 2(y – b).y′ = 0
⇒ (y – b). y′ = -x
⇒ (y – b) = -x/y′ …….(ii)
Substituting (ii) in (i),
x2 + (-x/y′)2 = 9
⇒ x2(1 + 1/(y′)2) = 9
⇒ x2 ((y′)2 + 1) = 9 (y′)2
⇒ (x2 – 9) (y′)2 + x2 = 0
Hence, this is the required differential equation.
Ques. Find the equation of a curve passing through (1, π/4) if the slope of the tangent to the curve at any point P (x, y) equals y/x – cos2(y/x). (4 marks)
Ans. According to given conditions,
dy/dx = y/x − cos2(y/x)............ (i)
This is a differential homogeneous equation.
Substituting y = vx in (i),
v + (x) dv/dx = v – cos2v
(x)dv/dx = − cos2v
sec2v dv = – dx/x
By merging both sides,
sec2v dv= – dx/x
tan v = – log x + c
tan (y/x) + log x = c.......... (ii)
Substituting x = 1 and y = /4,
tan (/4) + log 1 = c
1 + 0 = c
c = 1
c = 1 is substituted in (ii),
log x + tan (y/x) = 1
Ques. Find the standard solution for different calculations dy/dx = 1 + y2/1 + x2. (3 marks)
Ans. The given number is
dy/dx = 1 + y2/1 + x2
As 1 + y2 ≠ 0, so for variable dynamics, the given equation equation can be written as:
dy/1 + y2 = dx/1 + x2 ……. (i)
Add up the number (i) on both sides,
\(\int \frac{dy}{1+y^2} = \int \frac{dx}{1+x^2}\)tan-1y = tan-1x + C
This is a standard solution for the various calculations provided.
Ques. For each different equation provided, find a specific solution that satisfies the given condition: dy / dx = y tan x; y = 1 where x = 0 (3 marks)
Ans. dy / dx = y tan x
dy / y = tan x dx
Consolidation of both sides,
\(\int \frac{dy}{y} = \int tan x dx\)log y = log (sec x) + C
log y = log (C sec x)
⇒ y = C second x …… .. (i)
Now consider y = 1 where x = 0.
1 = C sec 0
1 = C (1)
C = 1
Inserting C = 1 in (i)
y = sec x
Therefore, this is a necessary solution for the given equation.
Ques. Determine the order and stems (if defined) of different numbers (y ′ ′) 2 + (y ″) 3 + (y ′) 4 + y5 = 0 (2 marks)
Ans. The given number is (y ′’′)2 + (y ″)3 + (y ′)4 + y5 = 0
The output of one of the highest values ââavailable in the range is y ′’′.
Therefore, its order is 3.
The different numbers given are the polynomial numbers y ′’′, y ′′, and y ′.
The highest power is raised at y′’′ i.e; 2.
Therefore, its degree is 2.
Ques. Make sure that the function y = a cos x + b sin x, where, a, b ∈ R is the solution of the divisive arithmetic d2y / dx2 + y = 0. (2 marks)
Ans. The given task is y = a cos x + b sin x ... (1)
Divide the two sides of the figure (1) in respect of x,
dy / dx = - a sinx + b cos x
d2y / dx2 = - a cos x - b sinx
LHS = d2y / dx2 + y
= - a cos x - b sinx + a cos x + b sin x
= 0
= RHS
Therefore, the given function is the solution of the given equation.
Ques. Construct a divisive number representing the family of curves y = a sin (x + b), where a, b are irrational constants. (2 marks)
Ans. Given,
y = a sin (x + b)… (1)
Divide the two sides of the figure (1) in respect of x,
dy / dx = a cos (x + b)… (2)
Divide again on both sides about x,
d2y / dx2 = - a sin (x + b)… (3)
Subtracting a and b from the scales (1), (2) and (3),
d2y / dx2 + y = 0… (4)
The above figure is free from such constants a and b.
This is a different number that is required.
Ques. Find the differential equation of the family of lines through the origin. (2 marks)
Ans. Let y = mx be the family of lines by origin.
Therefore, dy / dx = m
Removes m, (replaces m = y / x)
y = (dy / dx). x
Or
dy / dx - y = 0
Ques. Find the number of turns (1, π / 4) if the inclination of the tangent to the curve at any point P (x, y) is y / x - cos2 (y / x). (4 marks)
Ans. According to the given conditions,
dy / dx = y / x - cos2 (y / x) …………. (i)
This is a homogeneous differential equation.
Substituting y = vx for (i),
v + (x) dv / dx = v - cos2v
⇒ (x) dv / dx = - cos2v
⇒ sec2v dv = - dx / x
By combining both sides,
⇒sec2v dv = - dx / x
⇒ tan v = - log x + c
⇒ tan (y / x) + log x = c ………. (ii)
Enter x = 1 and y = / 4,
⇒ tan (/ 4) + log 1 = c
⇒ 1 + 0 = c
⇒ c = 1
Inserting c = 1 in (ii),
tan (y / x) + log x = 1
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments