
Namrata Das Exams Prep Master
Exams Prep Master
Integration is one of the most prominent parts of calculus, and it also has many applications in mathematics, physics, and chemistry. Integration corresponds to uniting, adding up, summing up, or collecting different parts of an equation to get the whole value. The integration is represented by the sign ( ∫ ). There are particularly two types of integration, Definite integral, and Indefinite integral. Here we will learn about definite integrals, their properties, and some important formulas.
Read Also: Conditional Probability
| Table of Content |
Key Terms: Definate integrals, indefinite integral, limit value of the integration, derivative of function, definite integral formula, surface integrals, balancing point.
Definite Integrals
[Click Here for Sample Questions]
When the integration takes place within two particular points, then it is called a definite integral. They have constant upper and lower limits, and the constants are supposed to be used to get the actual value of the integration between those limits. Definite integrals operate in the terms of indefinite integrals only. One of the main uses of definite integrals is that they tell us the area covered by the curve of a function above the x-axis.

The video below explains this:
Definite Integrals Video Lecture:
Concept Behind Definite Integral
[Click Here for Sample Questions]
Let’s check out what is the real concept behind definite integral. Definite integral is like a neighbor of the antiderivative and indefinite integral of a given function. Consider a given function f(x) which is continuous on a closed interval (a,b), and let the interval be divided into subintervals counting as ‘n’. These subintervals may or may not be of equal lengths. Let’s take an arbitrary domain value xi in each subinterval and its corresponding subinterval length is calculated. These ‘n’ products are added to calculate their sums. The sum is known as the Riemann sum which could be positive, negative and even zero depending upon the behavior of the function on a closed interval. Even though a definite integral provides the area above the x-axis, and the area is always positive, the value of the definite integral can be positive, negative, or zero.

We have several properties of definite integrals that we widely use for solutions which help in solving the problems easily.
Read more: Properties of Determinants
Definite Integral Formula
[Click Here for Sample Questions]
The formula for definite integral is given below-
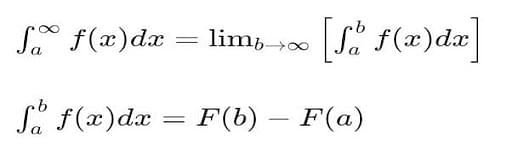
Here, ‘a’ and ‘b’ are the upper and lower limits. F(a) is the upper limit value and F(b) is the lower limit value of the integration.
The limit ‘a’ and ‘b’ represents an interval. It is not necessary that the lower limit has to be smaller and the upper limit has to be greater than the lower. You may call ‘a’ and ‘b’ as the interval of an integration.
Definite integral is also known as a Riemann integral when the ‘x’ is restricted to lie on the real line.
Read more: Geometric Progression (G. P.)
Definite Integration by Parts Formula
[Click Here for Sample Questions]
Definite integration by parts formula is generally used to integrate the product of two functions. The definite integration by parts formula is given as :
∫ p q dx = p ∫ q dx - ∫ p’ ( ∫ q dx ) dx
where
p is the function p(x),
q is the function q (x), and
p’ is the derivative of function p(x).
Read more: Application of Integral
Properties of Definite Integral Formula
[Click Here for Sample Questions]
Definite integral has some properties that we are going to study about. Some of those properties have been derived from the other. They also help us get the solution easily with fewer steps.
The properties of definite integral formula are given below:

Also Read:
| Related Articles | ||
|---|---|---|
| Tangents and Normals | Fundamental Theorem of Calculus | Integration by Partial Fractions |
| Methods of Integration | Integration by Parts | Bayes Theorem |
Formulas for Rational and Irrational Expressions

Read more: Integral Calculus
Formulas for Rational and Irrational Expressions
[Click Here for Sample Questions]

Applications of Definite Integral
[Click Here for Sample Questions]
Definite integrals can be commonly applied and be used for surface integrals, line integrals, and contour integrals. In mathematics, you can find the length, and area using definite integrals. Let’s learn more about this in detail-
Surface Area
It has been discussed already how we can find the surface area of a shape using definite integrals. Even if the shape is irregular, we can use definite integrals to find the surface area using double integration (which is out of your syllabus).

Area enclosed by two curves
One of the main applications of Definite integral is to find the area of a curve above the x-axis. In the same way, we can find the area between two curves defined by functions. If the graphs of the functions intersect each other. Finding the area enclosed can be done mostly by subtracting the smaller area from the greater one above the x-axis. You might have to evaluate two or more integrals.

Volume of 3-D shapes
Definite integrals not only can be used for finding surface area but also the volume of a shape. You will have to put them into unit slices and then find out the area of one slice and multiply it by the number of slices. The three dimensional volume can be obtained by slicing, disks, and washers. The type of the three dimensional shape plays an important role in the procedure.

Arc Length of Curves
One more application of definite integral is to find the arc length of a curve. Firstly, the arc length has to be approximated using line segments, and consequently a Riemann sum will be generated. Take the limit then put it in the definite integral formula.

Volume of Revolution
When a curve is revolving around an axis, then the volume of a solid made by its revolving around an axis can be derived as an intuitive extension of the surface area of revolution. The area and volume formula of the cylinder is similar to a revolving solid.

Physical Applications
Physical applications of integration are very common in the field of engineering and physics. If you have the density function of an object, then you can easily find the mass of that object using definite integrals. You can also calculate the Work done by integrating the known force function. Moreover, using definite integrals, you can calculate the force exerted on an object which is submerged in a liquid.
Finding the Centre of Mass and Moments
Moments and Centre of Mass of an object can be calculated with the help of definite integration. The concept of centre of mass is where the balancing point lies.
Also Read:
| Related Articles | ||
|---|---|---|
| Complex Numbers and Quadratic Equations | Geometric Mean (G.M.) | Bayes Theorem Formula |
| Sequence and Series | Arithmetic Progressions Revision Notes | Real Numbers Formula |
Things To Remember
[Click Here for Sample Questions]
- Integration being one of the most important parts of mathematics corresponds to a process in which the calculation of integrals takes place. In mathematics, Integrals can be prominently used to find quantities such as areas, volumes, displacement, and more. The term integral generally refers to definite integrals, while indefinite integrals can be seen that they are being used for antiderivatives. Integration is an important topic in Calculus.
- As we all are already aware that differentiation is a process in which we find the derivative of a function whereas integration is a process of finding the antiderivative of a function. You can clearly see that both of these processes are inverse of each other. Consequently, we can say that integration is the inverse process of differentiation or the other way round. Integration can also be referred to as anti-differentiation.
- When an integral has upper and lower limits, then it is called the definite integrals. It basically provides a closed interval within which the value of integration has to be found. The definite integral is also referred to as the Riemann Integral. For example,
![Integrals]()
here the function f(x) is being integrated with in the interval (a,b)
- The Definite Integral Formula is given here-
![Definite Integral Formula]()
- There are several properties of definite integrals given above. Do check them and remember them as they are very beneficial for future use. We will be using all the properties while solving questions at the end of this article.
- Application of the Definite integrals includes many useful topics. Some of them are finding surface area, surface area enclosed by two curves, calculating the volume of three dimensional shapes, measuring the arc length of curves, determining the volume of revolution of a shape, and locating the centre of mass and moments of an object. The definite integral is applied in physics and engineering fields in so many ways.
Read Also: Differentiation and Integral
Sample Questions
Ques: Solve \(\int\limits_2^6\)3dx (2 marks)
Ans:
Here, we have
Integration =
\(\int\limits_2^6\)3dx = 3\(\int\limits_2^6\)dx =36 - 2 = 3[4] = 12
Ques: Solve \(\int\limits_1^5\)(5x4-4x3+2x) dx (3 marks)
Ans: Here, we have been given that-
\(\int\limits_1^5\)(5x4-4x3+2x) dx
We have to integrate all the terms first
=[5x5/5 - 4x4/4 + 2x2/2]12
=[x5 - x4 + x2]12
=[(1)5 - (1)4 + (1)2 -{(2)5 - (2)4 + (2)2}]
=[ 1 - 1 + 1 - {32 - 16 + 4}]
=[1 - 20]
=[-19]
= -19
Ques: Solve \(\int\limits_{-3}^{-1}\)10x4dx (3 marks)
Ans: Here, we have an integration provided-
\(\int\limits_{-3}^{-1}\)10x4dx = [10x5/5]-1-3 = [2x5]-3-1 = 2[(-1)5 - (-3)5]
= 2[-1 -(-243)] = 2 [- 1 + 243]
= 2 [242]
= 484
Ques: Solve \(\int\limits_{1}^{2}\){x / (x² + 2)}dx (4 marks)
Ans: We have been given the integration as-
\(\int\limits_{1}^{2}\){x / (x2 + 2)}dx
We are going to use the substitution method for this-
Let's take the denominator to be
u =x2 + 2
du = 2x dx
xdx = du/2
The limits will also change. So, when x = 1 and 2, the value of u = 3 and 6 respectively.
The equation 1 can be written as-
I = [\(\int\limits_{3}^{6}\)(1/u)du]/2
I =12 [ logu]36
I = (log6 - log3)/2
I= [log(6/3)]/2
I =[log2]/2
Ques: Solve \(\int\limits_{2}^{4}\){8/√t−12√t3}dx (4 marks)
Ans: We have been given the integration to be
\(\int\limits_{1}^{4}\){8/√t−12√t3}dx
We can write the above equation to be:
14{8(t)-1/2 - 12 (t)3/2} dx
Now solving on the basis of just basic rules we would get:
I = [8(2)(t)1/2 - 12(2/5)(t)5/2]14
I = [16 (t)1/2 - 24/5(t)5/2]14
I = [16 (4)1/2 - 24/5 (4)5/2 - {16 (1)1/2 - 24/5 (1)5/2}]
I = [16(2) - 24/5(32) -{16 - 24/5}]
I = [32- 768/5 - 16 + 24/5]
I = [16 - 744/5]
I = [80 - 744]/5
I = -664/5
Ques: Solve\(\int\limits_{0}^{\pi/2}\)sin(t) − 2cos(t)dt (4 marks)
I =\(\int\limits_{0}^{\pi/2}\)sin(t) − 2cos(t)dt
I= [−7cos(t) − 2sin(t)]0\(\pi\)/2
I = [−7cos(\(\pi\)/2) − 2sin(\(\pi\)/2) - {−7cos(0) − 2sin(0)}]
I = [-7(0) - 2 (1) - {-7 (1)- 2 (0)}]
I =[0 - 2 + 7 + 0]
I = 5
Ques: Solve \(\int\limits_{0}^{2}\)exdx (3 marks)
\(\int\limits_{0}^{2}\)exdx
I = [ex]02 = e2 - e0
I = e2 -1
Ques: What are the main applications of definite integrals? (3 marks)
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:






Comments