
Content Strategy Manager
The determinant of a matrix is a scalar value that is calculated using the elements of a square matrix. It is a scaling factor for the transformation of a matrix. The determinant of a matrix is used to solve a system of linear equations, perform calculus operations, and calculate the inverse of a matrix.
- The square matrices can be a 2x2 matrix, 3x3 matrix, 4x4 matrix, or nxn matrix where the number of columns and rows are equal.
- Matrix is represented as det (A) or |A|.
- The determinant of a matrix is a function mapping each square matrix to a unique real or complex number.
- If A is the set of all square matrices and B is the set of all numbers, then the determinant function f (f: A → B) is defined as f(x) = y, where y denotes the determinant of matrix 'x'.
Also Read: Applications of Determinants and Matrices
| Table of Content |
Key Terms: Determinants, Square Matrices, column, Inverse of a matrix, Matrix, Complex number, Matrices, Linear equations
What are Determinants?
[Click Here for Sample Questions]
The determinant of a matrix is a scalar value calculated using a square matrix. In the case of every square matrix, A = \([a_{ij}]\) of order n, either a real or a complex number is associated, known as the determinant of the square matrix A, in which a = (i, j)th element of A.
If M is the set of square matrices, K is the set of real or complex numbers, f: M → K is defined by f (A) = k, where k ∈ K and A ∈ M, then f (A) is the determinant of A.
So, if \(A =\begin{bmatrix} a & b \\ c & d \end{bmatrix}\)
Then, the determinant of matrix A, denoted by |A| = \(\begin{vmatrix} a & b \\ c & d \end{vmatrix}\) = det A
The symbol of the determinant of a matrix is Δ. It is represented by two vertical lines, or det and the matrix name. eg. |A|, det(A), det A.
| Define matrix and determinant with example. A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. They are commonly used to represent systems of linear equations, transformations, and data structures. Example: \(A =\begin{bmatrix} 2 & 5 \\ 1 & -3\end{bmatrix}\) A determinant is a scalar value that can be computed from a square matrix. The determinant of a matrix is used to determine whether the matrix has an inverse or not, and it is also used to solve systems of linear equations. Example: The determinant of the above matrix can be calculated by(2 * -3) - (5 * 1) = -13 |
The video below explains this:
Matrices Detailed Video Explanation:
Read More:
| Important Topics | ||
|---|---|---|
| Identity Matrix | Matrix Multiplication | Operations on Matrices |
| Column Matrix | Symmetric Matrix | Symmetric & Skew-Symmetric Matrices |
Singular and Non-Singular Matrix
[Click Here for Previous Year Questions]
If the value of the determinants corresponding to the matrix is zero, it is said to be a square matrix, which means,
- If |A| = 0, then the matrix is Singular Matrix
- And if |A| \(\neq\)0, then the matrix is a non-singular matrix
Calculating the Value of a Determinant
[Click Here for Sample Questions]
For every square matrix [A]nxn, there is a determinant to the matrix that represents a unique value.
Step 1: Write out the matrix with its four entries. For example, a 2x2 matrix A can be written as:
A = [a b]
[c d]
Step 2: Multiply the entries in the main diagonal (the top-left to bottom-right diagonal) and subtract the product of the off-diagonal entries (the top-right to bottom-left diagonal). In other words, compute:
det(A) = ad - bc
Step 3: The resulting number is the determinant of the matrix.
For example, consider the matrix: \(A =\begin{bmatrix} 2 & 1 \\ 3 & 4 \end{bmatrix}\)
To calculate its determinant, we use the formula above: det(A) = (2 * 4) - (1 * 3) = 8 - 3 = 5.
Determinant of 2x2 Matrix
If we take det (A) = \(A =\begin{bmatrix} a11 & a21 \\ a22 & a12 \end{bmatrix}\)is the matrix of 2x2 order,
The above steps can be used to solve this matrix
So, det (A) = \(\bigtriangleup\) = a11a12 – a21a22
Solved ExampleCalculate the determinant of the matrix \(A =\begin{bmatrix} 2 & 4 \\ 1 & 3\end{bmatrix}\) |
Determinant of 3x3 Matrix
In the case of calculating the value of a 3x3 matrix, let us take an example:
det (A)
\(A = \begin{bmatrix}a & b & c\\[0.3em]d & e & f \\[0.3em]g & h & i\\[0.3em] \end{bmatrix}\)
Step 1: Find the three products of diagonal elements going from left to right:
a * e * i
b * f * g
c * d * h
Step 2: Find the three products of diagonal elements going from right to left:
c * e * g
b * d * i
a * f * h
Step 3: Subtract the sum of the products from step 3 from the sum of the products from step 2:
det = (a * e * i + b * f * g + c * d * h) - (c * e * g + b * d * i + a * f * h)
Step 4: Simplify and compute the result:
det = aei + bfg + cdh - ceg - bdi - afh
Step 5: The resulting value is the determinant of the 3x3 matrix.
The determinant is tried to be expanded along the row with the maximum number of zeroes in order to make the calculations easy.
Alternative Method
To find the determinant of a 3x3 matrix using the method of splitting into sub-matrices, follow these steps:
Step 1: Write down the matrix:
[a b c]
[d e f]
[g h i]
Step 2: Split the matrix into three 2x2 matrices, each of which excludes one row and one column of the original matrix:
A = [e f] B = [d f] C = [d e]
[h i] [g i] [g h]
Step 3: Compute the determinants of each sub-matrix:
det(A) = (e * i) - (f * h)
det(B) = (d * i) - (f * g)
det(C) = (d * h) - (e * g)
Step 4: Use the formula to calculate the determinant of the 3x3 matrix using the determinants of the sub-matrices:
det = a * det(A) - b * det(B) + c * det(C)
Step 5: Note that the signs of the second and fourth terms alternate between addition and subtraction.
Step 6: Simplify and compute the result:
det = a(ei - fh) - b(di - fg) + c(dh - eg)
The resulting value is the determinant of the 3x3 matrix.
The diagram given below consists of an example of a solved 3x3 matrix.
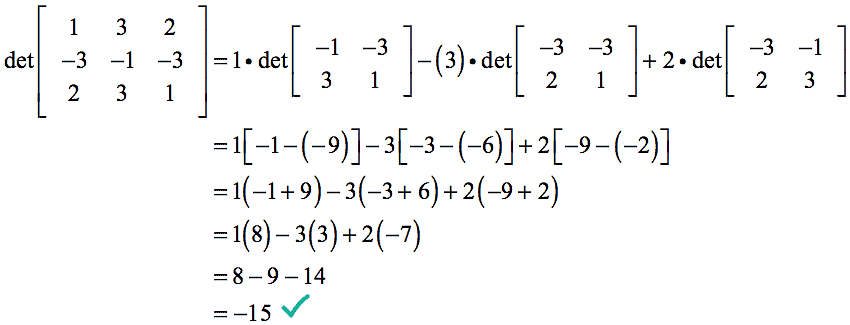
Solved ExampleCalculate the determinant of the matrix \(A =\begin{bmatrix} 6 & 1 & 1 \\ 4 & -2 & 5 \\ 2 & 8 & 7 \end{bmatrix} \) |
Discover about the Chapter video:
Determinants Detailed Video Explanation:
Also Read: Types of Matrices
Things to Remember
- In a square matrix, the number of rows is always equal to the number of columns.
- The 2x2 square matrix has two rows & two columns.
- For solving a 3x3 matrix, one row is needed to expand & then we can solve it as a 2x2 determinant.
- The determinant of a matrix always has a scalar value.
- The determinant of a matrix can be represented as |A| or det (A).
- Matrix is considered important in solving linear equations and useful for calculating the inverse of a matrix & calculus operations.
- There are usually 6 different ways of expanding a determinant of 3x3 order in which each of the three rows (R1, R2, R3) and three columns (C1, C2, C3) gives the same value. So, expanding any of one row or column will give out the same value.
Also Read:
Previous Year Questions
- Find the solution of the equation by using the determinant formula. [BITSAT 2006]
- Evaluate the determinant of the two matrices A and t. [BITSAT 2006]
- Apply determinant properties to solve the system of 3 equations. [AP EAPCET]
- Find the constant term in the polynomial by applying property of determinant. [KCET 2010]
- If two matrices are in A.P and find the range of the determinant. [CBSE Clas XII]
- A.adj(A) is equal to...[KCET 2007]
- If A=[α22α] | A^3|= 27∣A3∣=27then α is equal to….[KCET 2015]
- If A is a 3×3 nonsingular matrix and if |A | = 3, then |∣(2A)−1∣= _______[KCET 2010]
- If A is a matrix of order 3, such that A (adj A) = 10, then |adj A|=….[KCET 2014]
- If A is a square matrix of order 3 × 3, then ∣KA∣ is equal to….[KCET 2017]
Sample Questions
Ques. Evaluate the matrix \(A =\begin{bmatrix} 2 & 4 \\ -1 & 2 \end{bmatrix}\). (1 Mark)
Ans. In a 2x2 matrix, we can simply cross multiply to get the value of the determinant 2(2)-4(-1)
= 4+4 =8
Ques. Evaluate the value of \(A =\begin{bmatrix} 2 & 3 \\ 4 & 8 \end{bmatrix}\). (1 Mark)
Ans. In a 2x2 matrix, we can simply cross-multiply to get the value of the determinant of the matrix
= 2x8 – 4x3
= 16-12 = 4
|A| = 4
Ques. Evaluate the matrix \(A =\begin{bmatrix} x & x \\ 1x & -1x \end{bmatrix}\). (1 Mark)
Ans. In a 2x2 matrix, we can simply cross-multiply to get the value
= x (x) – (X+1) (x-1)
= \(x^2 – x^2 +1 \)
= 1
Ques. Find the cofactors and minors of det \(A =\begin{bmatrix} 1 & -2 \\ 4 & 3 \end{bmatrix}\) . (1 Mark)
Ans. \(M_{11} = 3 \quad M_{12} =4 \)
\(M_{21} = -2 \quad M_{22} = 1 \)
\(A_{11}= 3 \quad A_{12} = -4 \)
\(A_{21} = 2 \quad A_{22} = 1\)
Ques. Show if \(A =\begin{bmatrix} 1 & 1 \\ 4 & 8 \end{bmatrix}\) is singular or not. (1 Mark)
Ans. Here |A| = = 8-8 = 0
Hence, A is singular
Ques. Check whether (l + m + n) is a factor of the following determinant or not. [C.B.S.E. Sample Paper 2020] (2 Marks)
Ans. Given

Hence, (l + m + n) is a factor of a given determinant.
Ques. Using properties of determinants, prove the following: [C.B.S.E. 2019] (3 Marks)

Ans.

[Operating C3 → C3 + C2]
= (a + b) (a + c) (2) [c + b]
= 2(a + b) (b + c) (c + a) = RHS
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check Out:





Comments