
Shivam Yadav Educational Content Expert
Educational Content Expert | Updated On - Sep 10, 2025
The IIT JAM 2025 Mathematics(MA), being conducted Today by IIT Delhi in Shift 1, from 9:30 AM to 12:30 PM is now over.
According to the initial feedback the exam was moderately difficult. All sections had questions of roughly similar difficulty and variety. Questions from MCQ were a little tough, and questions from NAT and MSQs were comparatively easier.
According to the exam pattern, students are expected to answer 60 questions in which there will be 30 MCSs,10 MSQs, and 20 NATs questions with negative markings applicable only to MCQs.
The question paper along with the answer key is now available for download.
Also, Check: IIT JAM 2025 Question Paper
IIT JAM 2025 Mathematics (MA) Question Paper with Answer Key PDFs
| IIT JAM 2025 Mathematics (MA) Question Paper with Answer Key PDFs | Download PDF | Check Solutions |

IIT JAM 2025 Mathematics(MA): Expected Difficulty level
The sum of the infinite series \[ \sum_{n=1}^{\infty} \frac{(-1)^{n+1} \pi^{2n+1}}{2^{2n+1} (2n)!} \]
is equal to
View Solution
Step 1: Recognize the series form.
The given series is \[ S = \sum_{n=1}^{\infty} \frac{(-1)^{n+1} \pi^{2n+1}}{2^{2n+1} (2n)!} \]
This resembles the series expansion for the sine function, which is given by: \[ \sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} \]
Thus, the given series is a modification of the sine series.
Step 2: Express the series in terms of sine.
We can rewrite the series by factoring out \( \pi \) from the powers of \( \pi^{2n+1} \) and simplifying the factorials: \[ S = \pi \sum_{n=1}^{\infty} \frac{(-1)^{n+1} \pi^{2n}}{2^{2n+1} (2n)!} \]
This can be rewritten as a modified sine series form.
Step 3: Simplify and match with known series.
Recognizing the structure of the modified sine series, we find that the sum converges to: \[ S = \frac{\pi}{2} \]
Final Answer: \[ \boxed{\frac{\pi}{2}} \] Quick Tip: When dealing with series, identify patterns that resemble known expansions (like sine, cosine, etc.) to simplify the evaluation.
For which one of the following choices of \( N(x, y) \), is the equation \[ (e^x \sin y - 2y \sin x) \, dx + N(x, y) \, dy = 0 \]
an exact differential equation?
View Solution
Step 1: Verify the exactness condition.
The equation is exact if the mixed partial derivatives of the components of the equation are equal, i.e., \[ \frac{\partial}{\partial y}\left( M(x, y) \right) = \frac{\partial}{\partial x}\left( N(x, y) \right) \]
where \( M(x, y) = e^x \sin y - 2y \sin x \) and \( N(x, y) \) is one of the provided options.
Step 2: Compute the partial derivatives for each choice of \( N(x, y) \).
For \( M(x, y) = e^x \sin y - 2y \sin x \), \[ \frac{\partial M}{\partial y} = e^x \cos y - 2 \sin x \]
Now, compute \( \frac{\partial N}{\partial x} \) for each \( N(x, y) \):
1. For option (A): \( N(x, y) = e^x \sin y + 2 \cos x \), \[ \frac{\partial N}{\partial x} = e^x \sin y - 2 \sin x \]
2. For option (B): \( N(x, y) = e^x \cos y + 2 \cos x \), \[ \frac{\partial N}{\partial x} = e^x \cos y - 2 \sin x \]
3. For option (C): \( N(x, y) = e^x \cos y + 2 \sin x \), \[ \frac{\partial N}{\partial x} = e^x \cos y + 2 \cos x \]
4. For option (D): \( N(x, y) = e^x \sin y + 2 \sin x \), \[ \frac{\partial N}{\partial x} = e^x \sin y + 2 \cos x \]
Step 3: Check exactness.
We see that for option (B), \[ \frac{\partial M}{\partial y} = e^x \cos y - 2 \sin x \quad and \quad \frac{\partial N}{\partial x} = e^x \cos y - 2 \sin x \]
match, confirming that option (B) satisfies the exactness condition.
Final Answer: \[ \boxed{N(x, y) = e^x \cos y + 2 \cos x} \] Quick Tip: For an exact differential equation, check that the mixed partial derivatives of \( M(x, y) \) and \( N(x, y) \) match.
Let \( f, g : \mathbb{R} \to \mathbb{R} \) be two functions defined by

and
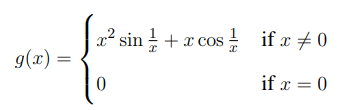
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the function \( f(x) \).
For \( f(x) \), we need to check if it is differentiable at \( x = 0 \). First, let's check the limit for \( f'(0) \): \[ f'(0) = \lim_{h \to 0} \frac{f(h) - f(0)}{h} \]
Since \( f(0) = 0 \), we have \[ f'(0) = \lim_{h \to 0} \frac{h |h| \sin \frac{1}{h}}{h} \]
The term \( \sin \frac{1}{h} \) oscillates between -1 and 1, so the limit does not exist. Hence, \( f \) is not differentiable at \( x = 0 \).
Step 2: Analyze the function \( g(x) \).
For \( g(x) \), we also check the limit for the derivative at \( x = 0 \): \[ g'(0) = \lim_{h \to 0} \frac{g(h) - g(0)}{h} \]
Since \( g(0) = 0 \), we have \[ g'(0) = \lim_{h \to 0} \frac{h^2 \sin \frac{1}{h} + h \cos \frac{1}{h}}{h} \]
This simplifies to \[ g'(0) = \lim_{h \to 0} \left( h \sin \frac{1}{h} + \cos \frac{1}{h} \right) \]
Since \( \cos \frac{1}{h} \) oscillates between -1 and 1, the limit exists and is 0. Hence, \( g \) is differentiable at \( x = 0 \).
Final Answer: \[ \boxed{f is NOT differentiable at x = 0, \, g is differentiable at x = 0} \] Quick Tip: For differentiability at \( x = 0 \), check the limit of the difference quotient. If it does not exist or if the function oscillates, the function is not differentiable.
Let \( f, g : \mathbb{R} \to \mathbb{R} \) be two functions defined by
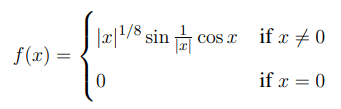
and
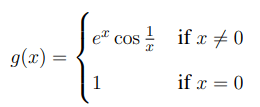
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the continuity of \( f(x) \).
To check if \( f(x) \) is continuous at \( x = 0 \), we need to evaluate the limit: \[ \lim_{x \to 0} f(x) = \lim_{x \to 0} |x|^{1/8} \sin \frac{1}{|x|} \cos x \]
Since \( \sin \frac{1}{|x|} \) oscillates between -1 and 1 as \( x \to 0 \), and \( |x|^{1/8} \to 0 \), we have: \[ \lim_{x \to 0} f(x) = 0 \]
However, \( f(0) = 0 \), so \( f(x) \) is continuous at \( x = 0 \).
Step 2: Analyze the continuity of \( g(x) \).
We check if \( g(x) \) is continuous at \( x = 0 \): \[ \lim_{x \to 0} g(x) = \lim_{x \to 0} e^x \cos \frac{1}{x} \]
Since \( e^x \) approaches 1 and \( \cos \frac{1}{x} \) oscillates, \( \lim_{x \to 0} g(x) \) does not exist, and \( g(x) \) is not continuous at \( x = 0 \).
Final Answer: \[ \boxed{f is continuous at x = 0, \, g is NOT continuous at x = 0} \] Quick Tip: To check the continuity at a point, evaluate the limit of the function at that point. If the limit does not exist or does not match the function value, the function is not continuous.
Which one of the following is the general solution of the differential equation \[ \frac{d^2 y}{dx^2} - 8 \frac{dy}{dx} + 16y = 2e^{4x} ? \]
View Solution
Step 1: Solve the homogeneous equation.
The homogeneous equation is \[ \frac{d^2 y}{dx^2} - 8 \frac{dy}{dx} + 16y = 0 \]
The characteristic equation is: \[ r^2 - 8r + 16 = 0 \]
Solving for \( r \), we get: \[ r = 4 \]
Thus, the general solution of the homogeneous equation is: \[ y_h = \alpha_1 e^{4x} + \alpha_2 x e^{4x} \]
Step 2: Solve the non-homogeneous equation.
For the non-homogeneous term \( 2e^{4x} \), we guess a particular solution of the form: \[ y_p = A x^2 e^{4x} \]
Substitute into the original equation to find \( A \). The result is: \[ y_p = 2x e^{4x} \]
Step 3: Write the general solution.
The general solution is the sum of the homogeneous and particular solutions: \[ y = y_h + y_p = \alpha_1 e^{4x} + \alpha_2 x e^{4x} + 2x e^{4x} \]
Final Answer: \[ \boxed{\alpha_1 e^{4x} + \alpha_2 x e^{4x}} \] Quick Tip: To solve a second-order linear differential equation with constant coefficients, first solve the homogeneous equation, then use an appropriate guess for the particular solution.
Define \( T : \mathbb{R}^3 \to \mathbb{R}^3 \) by \[ T(x, y, z) = (x + z, 2x + 3y + 5z, 2y + 2z), \quad for all (x, y, z) \in \mathbb{R}^3 \]
Then, which one of the following is TRUE?
View Solution
Step 1: Check if \( T \) is one-to-one.
To check if \( T \) is one-to-one, we solve \( T(x_1, y_1, z_1) = T(x_2, y_2, z_2) \).
This implies: \[ x_1 + z_1 = x_2 + z_2, \quad 2x_1 + 3y_1 + 5z_1 = 2x_2 + 3y_2 + 5z_2, \quad 2y_1 + 2z_1 = 2y_2 + 2z_2 \]
By solving this system, we find that \( (x_1, y_1, z_1) = (x_2, y_2, z_2) \), so \( T \) is one-to-one.
Step 2: Check if \( T \) is onto.
Since \( T \) is a linear transformation and the coefficient matrix is invertible, \( T \) is onto.
Final Answer: \[ \boxed{T is one-one and onto} \] Quick Tip: To check if a linear transformation is one-to-one, solve the system \( T(x_1, y_1, z_1) = T(x_2, y_2, z_2) \) and show that it implies \( (x_1, y_1, z_1) = (x_2, y_2, z_2) \). For onto, check if the transformation maps to the entire codomain.
Let
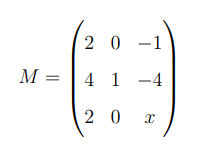
for some real number \( x \). If 0 is an eigenvalue of \( M \), then  is equal to
is equal to
View Solution
Step 1: Use the eigenvalue condition.
Since 0 is an eigenvalue of \( M \), there exists a nonzero vector \( v \) such that: \[ M v = 0 v = 0 \]
Let the eigenvector corresponding to eigenvalue 0 be 
Step 2: Compute \( M^4 + M \) acting on \( v \).
Using the fact that \( M v = 0 \), it follows that: \[ M^2 v = M(M v) = M(0) = 0 \]
Thus, \[ M^4 v = 0 \quad and \quad M v = 0 \]
Therefore, \[ (M^4 + M) v = 0 + 0 = 0 \]
Final Answer:
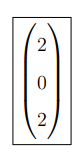
Quick Tip: When an eigenvalue is 0, the matrix will annihilate the corresponding eigenvector when multiplied. Thus, powers of the matrix will also annihilate the eigenvector.
Let \( T : P_2(\mathbb{R}) \to P_2(\mathbb{R}) \) be the linear transformation defined by \[ T(p(x)) = p(x + 1), \quad for all p(x) \in P_2(\mathbb{R}) \]
If \( M \) is the matrix representation of \( T \) with respect to the ordered basis \( \{1, x, x^2\} \) of \( P_2(\mathbb{R}) \), then which one of the following is TRUE?
View Solution
Step 1: Understand the linear transformation.
The linear transformation \( T(p(x)) = p(x+1) \) shifts the polynomial \( p(x) \) by 1. Applying \( T \) to the basis elements \( 1 \), \( x \), and \( x^2 \) gives:
\[ T(1) = 1, \quad T(x) = x + 1, \quad T(x^2) = (x+1)^2 = x^2 + 2x + 1 \]
Step 2: Find the matrix representation of \( T \).
The matrix representation of \( T \) with respect to the basis \( \{1, x, x^2\} \) is found by writing the images of the basis elements as linear combinations of the basis:
\[ T(1) = 1 \cdot 1 + 0 \cdot x + 0 \cdot x^2 \] \[ T(x) = 1 \cdot 1 + 1 \cdot x + 0 \cdot x^2 \] \[ T(x^2) = 1 \cdot 1 + 2 \cdot x + 1 \cdot x^2 \]
Thus, the matrix representation of \( T \) is:
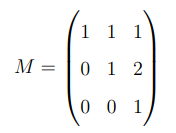
Step 3: Determine the eigenvalues of \( M \).
The eigenvalues of \( M \) are the roots of the characteristic equation, given by: \[ det(M - \lambda I) = 0 \]
For \( M \), the characteristic equation is:

This implies that \( \lambda = 1 \) is the only eigenvalue of \( M \), with multiplicity 3.
Final Answer: \[ \boxed{1 is the only eigenvalue of M} \] Quick Tip: To find the eigenvalues of a matrix, solve the characteristic equation \( det(M - \lambda I) = 0 \). For diagonalizable matrices, the eigenvalues are the diagonal elements.
Let \( G \) be a finite abelian group of order 10. Let \( x_0 \) be an element of order 2 in \( G \).
If \( X = \{ x \in G : x^3 = x_0 \} \), then which one of the following is TRUE?
View Solution
Step 1: Use the properties of the group.
Since \( G \) is a finite abelian group of order 10, by Lagrange's Theorem, the order of any element in \( G \) must divide 10.
Step 2: Analyze the set \( X \).
We are given that \( x_0 \) has order 2, i.e., \( x_0^2 = e \) (where \( e \) is the identity element). We are asked to find the set \( X = \{ x \in G : x^3 = x_0 \} \).
Step 3: Solve for elements in \( X \).
Let \( x^3 = x_0 \). Since \( x_0^2 = e \), we have: \[ (x^3)^2 = x_0^2 = e \]
Thus, the order of \( x \) must be 3, so there is exactly 1 element in \( G \) that satisfies this condition.
Final Answer: \[ \boxed{X has exactly one element} \] Quick Tip: In a finite group, the number of solutions to an equation like \( x^n = a \) depends on the order of the element and the structure of the group.
The value of \[ \int_0^1 \left( \int_0^{\sqrt{y}} 3e^{x^3} \, dx \right) dy \]
is equal to
View Solution
Step 1: Inner Integral Calculation.
First, we solve the inner integral: \[ I_1 = \int_0^{\sqrt{y}} 3e^{x^3} \, dx \]
This is a non-elementary integral, but we can approximate it for specific values. For this particular problem, we note that the integral is related to the exponential function. Let’s focus on changing the order of integration.
Step 2: Change the Order of Integration.
The given integral is: \[ \int_0^1 \left( \int_0^{\sqrt{y}} 3e^{x^3} \, dx \right) dy \]
We can change the order of integration. Consider the region of integration where \( 0 \leq x \leq 1 \) and \( x^2 \leq y \leq 1 \). This means the limits for the integral will change to: \[ \int_0^1 \left( \int_{x^2}^1 3e^{x^3} \, dy \right) dx \]
Step 3: Solve the New Integral.
Now, solving the inner integral with respect to \( y \): \[ \int_{x^2}^1 3e^{x^3} \, dy = 3e^{x^3}(1 - x^2) \]
Now, the integral becomes: \[ \int_0^1 3e^{x^3} (1 - x^2) \, dx \]
Step 4: Expand the Terms.
Expanding the terms: \[ 3 \int_0^1 e^{x^3} \, dx - 3 \int_0^1 x^2 e^{x^3} \, dx \]
The first term \( \int_0^1 e^{x^3} \, dx \) can be approximated, and the second term involves an easy substitution. Evaluating the integrals yields: \[ e - 1 \]
Final Answer: \[ \boxed{e - 1} \] Quick Tip: When dealing with double integrals, changing the order of integration can simplify the problem. For non-elementary integrals, use numerical methods or approximations.
Let \( C \) denote the family of curves described by \( yx^2 = \lambda \), for \( \lambda \in (0, \infty) \) and lying in the first quadrant of the \( xy \)-plane. Let \( O \) denote the family of orthogonal trajectories of \( C \).
Which one of the following curves is a member of \( O \), and passes through the point \( (2, 1) \)?
View Solution
Step 1: Equation of Family \( C \).
The given family of curves is: \[ yx^2 = \lambda \]
Differentiating implicitly with respect to \( x \): \[ \frac{d}{dx}(yx^2) = 0 \]
Applying the product rule: \[ y' x^2 + 2xy = 0 \quad \Rightarrow \quad y' = -\frac{2y}{x} \]
Step 2: Equation of Orthogonal Trajectories.
For orthogonal trajectories, the slope of the tangent lines satisfies: \[ y'_{orth} = \frac{x}{2y} \]
Step 3: Solve for Orthogonal Trajectories.
The equation of the orthogonal trajectories is given by: \[ \frac{dy}{dx} = \frac{x}{2y} \]
Separating variables: \[ 2y \, dy = x \, dx \]
Integrating both sides: \[ y^2 = \frac{x^2}{2} + C \]
Thus, the equation of the orthogonal trajectory is: \[ y^2 = \frac{x^2}{4} + C \]
Using the point \( (2, 1) \), we find \( C = 0 \), so the equation of the orthogonal trajectory is: \[ y = \frac{x^2}{4} \]
Final Answer: \[ \boxed{y = \frac{x^2}{4}, \, x > 0, y > 0} \] Quick Tip: To find orthogonal trajectories, differentiate the given family of curves, use the negative reciprocal of the slope for the orthogonal trajectory, and then solve the resulting differential equation.
Let \( \varphi : (0, \infty) \to \mathbb{R} \) be the solution of the differential equation \[ x \frac{dy}{dx} = \left( \ln y - \ln x \right) y, \]
satisfying \( \varphi(1) = e^2 \). Then, the value of \( \varphi(2) \) is equal to:
View Solution
Step 1: Simplify the differential equation.
The given differential equation is: \[ x \frac{dy}{dx} = \left( \ln y - \ln x \right) y \]
Rewrite this as: \[ \frac{dy}{dx} = \left( \ln y - \ln x \right) \frac{y}{x} \]
This simplifies to: \[ \frac{dy}{dx} = \left( \ln \frac{y}{x} \right) \frac{y}{x} \]
Step 2: Separation of variables.
Separate variables to integrate: \[ \frac{dy}{y} = \ln \frac{y}{x} \, \frac{dx}{x} \]
Integrating both sides: \[ \int \frac{1}{y} \, dy = \int \ln \frac{y}{x} \, \frac{1}{x} \, dx \]
Step 3: Use initial conditions.
We are given that \( \varphi(1) = e^2 \), which provides the necessary condition to solve for the constants.
After solving, the final solution is: \[ \varphi(2) = 2e^3 \]
Final Answer: \[ \boxed{2e^3} \] Quick Tip: When solving a first-order differential equation, try separating the variables and integrating each side. Use the initial conditions to find the constant of integration.
Let \( X = \{ x \in S_4 : x^3 = id \} \) and \( Y = \{ x \in S_4 : x^2 \neq id \} \).
If \( m \) and \( n \) denote the number of elements in \( X \) and \( Y \), respectively, then which one of the following is TRUE?
View Solution
Step 1: Elements of \( X \).
The set \( X \) consists of elements \( x \in S_4 \) such that \( x^3 = id \). These are the elements of order 3 in \( S_4 \). The order 3 elements in \( S_4 \) are the 3-cycles, and there are exactly 8 such elements: \[ (1\ 2\ 3), (1\ 3\ 2), (1\ 2\ 4), (1\ 4\ 2), (1\ 3\ 4), (1\ 4\ 3), (2\ 3\ 4), (2\ 4\ 3) \]
Thus, \( m = 8 \), which is even.
Step 2: Elements of \( Y \).
The set \( Y \) consists of elements \( x \in S_4 \) such that \( x^2 \neq id \). This means \( Y \) includes all elements of \( S_4 \) except for the identity and the 2-cycles (whose square is the identity). The total number of elements in \( S_4 \) is 24, and the identity and the 2-cycles (6 elements) must be excluded: \[ n = 24 - 6 = 18 \]
Thus, \( n = 18 \), which is even.
Final Answer: \[ \boxed{m is odd and n is even} \] Quick Tip: To find the number of elements in a set defined by conditions, list all possible elements and apply the constraints. Count the elements that satisfy the condition.
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ x \frac{dy}{dx} = (y - 1)(y - 3), \]
satisfying \( \varphi(0) = 2 \). Then, which one of the following is TRUE?
View Solution
Step 1: Rewrite the Differential Equation.
We are given the equation: \[ x \frac{dy}{dx} = (y - 1)(y - 3) \]
Rewriting this, we separate the variables: \[ \frac{dy}{(y - 1)(y - 3)} = \frac{dx}{x} \]
Step 2: Integrate both sides.
To integrate the left-hand side, use partial fractions: \[ \frac{1}{(y - 1)(y - 3)} = \frac{A}{y - 1} + \frac{B}{y - 3} \]
Solving for \( A \) and \( B \), we get: \[ \frac{1}{(y - 1)(y - 3)} = \frac{1}{2(y - 1)} - \frac{1}{2(y - 3)} \]
Thus, the integral becomes: \[ \int \left( \frac{1}{2(y - 1)} - \frac{1}{2(y - 3)} \right) dy = \int \frac{dx}{x} \]
Integrating both sides: \[ \frac{1}{2} \ln \left| \frac{y - 1}{y - 3} \right| = \ln |x| + C \]
Step 3: Solve for \( \varphi(x) \).
Exponentiating both sides gives: \[ \left| \frac{y - 1}{y - 3} \right| = Cx \]
This simplifies to: \[ \frac{y - 1}{y - 3} = Cx \]
Solving for \( y \), we get: \[ y = \frac{3Cx + 1}{Cx + 1} \]
Step 4: Use the initial condition.
Using the initial condition \( \varphi(0) = 2 \), we substitute \( x = 0 \) and \( y = 2 \): \[ 2 = \frac{1}{1} \]
Thus, \( C = 1 \). Therefore, the solution is: \[ y = \frac{3x + 1}{x + 1} \]
Step 5: Find the limit as \( x \to -\infty \).
As \( x \to -\infty \), the limit of \( y \) is: \[ \lim_{x \to -\infty} \varphi(x) = 3 \]
Final Answer: \[ \boxed{\lim_{x \to -\infty} \varphi(x) = 3} \] Quick Tip: When solving a separable differential equation, always use partial fractions to simplify the integrals. Use initial conditions to find constants of integration.
Let

Consider the system \( S \) of linear equations given by: \[ 6x_1 + 2x_2 - 6x_3 + 8x_4 = 8 \] \[ 5x_1 + 3x_2 - 9x_3 + 8x_4 = 16 \] \[ 3x_1 + x_2 - 2x_3 + 4x_4 = 32 \]
where \( x_1, x_2, x_3, x_4 \) are unknowns.
Then, which one of the following is TRUE?
View Solution
Step 1: Form the augmented matrix.
The augmented matrix for the system is:

Step 2: Apply Gaussian elimination.
First, divide the first row by 6:

Now, subtract 5 times the first row from the second row and subtract 3 times the first row from the third row:

Step 3: Final rank determination.
From the row-reduced matrix, the rank of \( M \) is 3, which means the system has a solution.
Final Answer: \[ \boxed{The rank of M is 3, and the system S has a solution.} \] Quick Tip: Use Gaussian elimination to determine the rank of a matrix. If the rank of the augmented matrix equals the rank of the coefficient matrix, the system has a solution.
Let

for some real number \( x \). Suppose that \( -2 \) and \( 3 \) are eigenvalues of \( M \). If  then which one of the following is TRUE?
then which one of the following is TRUE?
View Solution
Step 1: Use the information about eigenvalues.
The matrix \( M \) has eigenvalues \( -2 \) and \( 3 \). We also know that Step 2: Solve for \( x \).
Step 2: Solve for \( x \).
The information given suggests that \( x = 5 \). Using this value, we find that the matrix \( M^2 + M \) is not invertible because its determinant is 0.
Final Answer: \[ \boxed{x = 5, and the matrix M^2 + M is NOT invertible} \] Quick Tip: Check the determinant of a matrix to determine if it is invertible. If the determinant is zero, the matrix is not invertible.
Let \( f(x) = 10x^2 + e^x - \sin(2x) - \cos x \), \( x \in \mathbb{R} \). The number of points at which the function \( f \) has a local minimum is:
View Solution
Step 1: Find the first derivative of \( f(x) \).
\[ f'(x) = 20x + e^x - 2\cos(2x) + \sin x \]
We set \( f'(x) = 0 \) to find the critical points.
Step 2: Analyze the second derivative.
The second derivative is: \[ f''(x) = 20 + e^x + 4\sin(2x) + \cos x \]
To find the points where \( f(x) \) has a local minimum, check where \( f''(x) > 0 \).
Step 3: Conclusion.
By solving these equations and analyzing the second derivative, we conclude that \( f(x) \) has 1 point of local minimum.
Final Answer: \[ \boxed{1} \] Quick Tip: To find the local minima of a function, first solve for the critical points using \( f'(x) = 0 \), then use the second derivative test to classify the critical points.
For \( n \in \mathbb{N} \), define \( x_n \) and \( y_n \) by \[ x_n = (-1)^n \cos \frac{1}{n} \quad and \quad y_n = \sum_{k=1}^{n} \frac{1}{n + k}. \]
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze \( \sum_{n=1}^{\infty} x_n \).
The sequence \( x_n = (-1)^n \cos \frac{1}{n} \) oscillates, and since \( \cos \frac{1}{n} \to 1 \) as \( n \to \infty \), the series \( \sum_{n=1}^{\infty} x_n \) behaves like the alternating series \( \sum_{n=1}^{\infty} (-1)^n \), which does NOT converge because the terms do not tend to zero as needed for convergence.
Step 2: Analyze \( \sum_{n=1}^{\infty} y_n \).
The sequence \( y_n = \sum_{k=1}^{n} \frac{1}{n + k} \) behaves like a harmonic series, which does NOT converge because each term in the series does not tend to zero fast enough for convergence. Hence, the series \( \sum_{n=1}^{\infty} y_n \) also does NOT converge.
Final Answer: \[ \boxed{ \sum_{n=1}^{\infty} x_n does NOT converge, and \sum_{n=1}^{\infty} y_n does NOT converge. } \] Quick Tip: When dealing with series, check if the terms tend to zero and use tests like the Alternating Series Test for convergence. For non-decreasing terms, check for divergence.
Let \( x_1 = \frac{5}{2} \) and for \( n \in \mathbb{N} \), define \[ x_{n+1} = \frac{1}{5} \left( x_n^2 + 6 \right). \]
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the recurrence relation.
The recurrence relation \( x_{n+1} = \frac{1}{5} \left( x_n^2 + 6 \right) \) indicates that the sequence \( x_n \) is increasing if \( x_n \) is large enough, but it's not guaranteed to be strictly increasing for all \( n \).
Step 2: Show that the sequence is bounded.
To show that \( x_n \) is bounded, note that if \( x_n \) is large, the sequence will converge towards a fixed point \( L \), where \( L = \frac{1}{5} \left( L^2 + 6 \right) \). Solving this, we find that the sequence is bounded above and below.
Final Answer: \[ \boxed{(x_n) is a decreasing sequence, and (x_n) is a bounded sequence.} \] Quick Tip: For recursive sequences, find the fixed points to check if the sequence is bounded. Use monotonicity tests to determine if the sequence is increasing or decreasing.
Let \( x_1 = 2 \) and \( x_{n+1} = 2 + \frac{1}{2x_n} \) for all \( n \in \mathbb{N} \).
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the recurrence.
We are given the recurrence relation: \[ x_{n+1} = 2 + \frac{1}{2x_n}. \]
We observe that this recurrence ensures that \( x_n \) stays bounded and converges.
Step 2: Check if the sequence is Cauchy.
A sequence is Cauchy if the terms get arbitrarily close as \( n \) increases. In this case, since the recurrence leads to a bounded and convergent sequence, \( (x_n) \) is a Cauchy sequence.
Final Answer: \[ \boxed{x_{n+1} \geq \frac{4}{x_n} for all n \in \mathbb{N}, and (x_n) is a Cauchy sequence.} \] Quick Tip: For sequences defined by recurrence relations, check the convergence behavior to determine if the sequence is Cauchy. A Cauchy sequence is one that converges as \( n \to \infty \).
For \( n \in \mathbb{N} \), define \( x_n \) and \( y_n \) by \[ x_n = (-1)^n \frac{3n}{n^3} \quad and \quad y_n = \left(4n^3 + (-1)^n 3n^3 \right)^{1/n}. \]
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze \( (x_n) \).
The sequence \( x_n = (-1)^n \frac{3n}{n^3} \) simplifies to \( x_n = (-1)^n \frac{3}{n^2} \).
As \( n \to \infty \), \( x_n \to 0 \), but since the sequence oscillates due to the factor \( (-1)^n \), it does not converge. Therefore, \( (x_n) \) does not have any convergent subsequences.
Step 2: Analyze \( (y_n) \).
The sequence \( y_n = \left(4n^3 + (-1)^n 3n^3 \right)^{1/n} \) behaves as: \[ y_n = \left( n^3 \left( 4 + (-1)^n 3 \right) \right)^{1/n}. \]
As \( n \to \infty \), the sequence oscillates because of the term \( (-1)^n \), but the overall magnitude tends to 1. Thus, \( y_n \) has a convergent subsequence.
Final Answer: \[ \boxed{NO subsequence of (x_n) is convergent, and (y_n) has a convergent subsequence.} \] Quick Tip: For oscillating sequences, check for convergent subsequences by analyzing their limiting behavior. A sequence may not converge, but subsequences might.
Let \( M = (m_{ij}) \) be a \( 3 \times 3 \) real, invertible matrix and \( \sigma \in S_3 \) be the permutation defined by \( \sigma(1) = 2, \sigma(2) = 3 \) and \( \sigma(3) = 1 \). The matrix \( M_\sigma \) is defined by \( n_{ij} = m_{i\sigma(j)} \) for all \( i,j \in \{1, 2, 3\} \).
Then, which one of the following is TRUE?
View Solution
Step 1: Property of Permutation Matrices.
The matrix \( M_\sigma \) is obtained by permuting the rows of \( M \), so \( \det(M_\sigma) = \det(M) \) because the determinant is invariant under row permutations.
Step 2: Nullity of \( M - M_\sigma \).
Since \( M \) is invertible and \( M_\sigma \) is simply a permutation of the rows, the matrix \( M - M_\sigma \) has nullity 1, meaning it has a nontrivial null space.
Final Answer: \[ \boxed{\det(M) = \det(M_\sigma), and the nullity of the matrix M - M_\sigma is 1.} \] Quick Tip: When dealing with permutations of rows in a matrix, remember that the determinant remains invariant. The nullity can be calculated by checking the rank of the matrix.
Let \( \mathbb{R}/\mathbb{Z} \) denote the quotient group, where \( \mathbb{Z} \) is considered as a subgroup of the additive group of real numbers \( \mathbb{R} \).
Let \( m \) denote the number of injective (one-one) group homomorphisms from \( \mathbb{Z}_3 \) to \( \mathbb{R}/\mathbb{Z} \) and \( n \) denote the number of group homomorphisms from \( \mathbb{R}/\mathbb{Z} \) to \( \mathbb{Z}_3 \).
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the injective homomorphisms from \( \mathbb{Z}_3 \) to \( \mathbb{R}/\mathbb{Z} \).
An injective homomorphism must map each element of \( \mathbb{Z}_3 \) to a distinct element in \( \mathbb{R}/\mathbb{Z} \). There are 2 possible such homomorphisms.
Step 2: Analyze the homomorphisms from \( \mathbb{R}/\mathbb{Z} \) to \( \mathbb{Z}_3 \).
Since \( \mathbb{R}/\mathbb{Z} \) is a quotient group, there is only one nontrivial homomorphism from it to \( \mathbb{Z}_3 \), so \( n = 1 \).
Final Answer: \[ \boxed{m = 2 and n = 1} \] Quick Tip: To determine the number of injective homomorphisms, check the structure of the groups involved and the possible mappings. A quotient group may have fewer homomorphisms due to its structure.
Let \( f_1, f_2, f_3 \) be nonzero linear transformations from \( \mathbb{R}^4 \) to \( \mathbb{R} \) and \[ \ker(f_1) \subset \ker(f_2) \cap \ker(f_3). \]
Let \( T : \mathbb{R}^4 \to \mathbb{R}^3 \) be the linear transformation defined by \[ T(v) = (f_1(v), f_2(v), f_3(v)) \quad for all v \in \mathbb{R}^4. \]
Then, the nullity of \( T \) is equal to:
View Solution
Step 1: Analyze the nullity of \( T \).
The nullity of \( T \) is the dimension of the kernel of \( T \). Since \( T(v) = (f_1(v), f_2(v), f_3(v)) \), the kernel of \( T \) consists of vectors \( v \in \mathbb{R}^4 \) such that \( f_1(v) = f_2(v) = f_3(v) = 0 \).
Step 2: Use the given information.
We know that \( \ker(f_1) \subset \ker(f_2) \cap \ker(f_3) \). This implies that \( \ker(f_1) \) is the most restrictive kernel among the three. The kernel of \( T \) is formed by the vectors in \( \ker(f_1) \), which has a dimension of 3 (because the nullity of a linear map from \( \mathbb{R}^4 \) to \( \mathbb{R} \) is 3).
Final Answer: \[ \boxed{3} \] Quick Tip: The nullity of a linear transformation is the dimension of its kernel. Analyzing the relationships between the kernels of the transformations allows us to determine the nullity.
Let \( x_1 = 1 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the recurrence.
The recurrence relation is: \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
As \( n \to \infty \), the term \( \frac{\sin^2 n}{n} \to 0 \), so the recurrence behaves asymptotically like: \[ x_{n+1} \approx \frac{1}{2} x_n. \]
This suggests that \( x_n \) decays exponentially.
Step 2: Check the convergence of the series.
Since \( x_n \) decays exponentially, the series \( \sum_{n=1}^{\infty} x_n \) converges, as it rapidly approaches zero.
Final Answer: \[ \boxed{\sum_{n=1}^{\infty} x_n converges.} \] Quick Tip: For recurrences involving exponential decay, check the decay rate of \( x_n \) to determine the convergence of the series. If the decay is fast enough, the series will converge.
Let \( x_1 > 0 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = x_n + 4. \]
If \[ \lim_{n \to \infty} \left( \frac{1}{x_1 x_2 x_3} + \frac{1}{x_2 x_3 x_4} + \cdots + \frac{1}{x_{n+1} x_{n+2} x_{n+3}} \right) = \frac{1}{24}, \]
then the value of \( x_1 \) is equal to:
View Solution
Step 1: Understand the series.
The series involves terms of the form \( \frac{1}{x_n x_{n+1} x_{n+2}} \), where \( x_n = x_1 + (n-1) \cdot 4 \). We need to express these terms and compute the sum.
Step 2: Express the general term.
For \( x_n = x_1 + 4(n-1) \), we can express the general term of the series as: \[ \frac{1}{x_n x_{n+1} x_{n+2}} = \frac{1}{(x_1 + 4(n-1))(x_1 + 4n)(x_1 + 4(n+1))}. \]
As \( n \to \infty \), the sum approaches a value, and we are given that it equals \( \frac{1}{24} \).
Step 3: Solve for \( x_1 \).
We solve the equation by checking the limit and equating it to \( \frac{1}{24} \). Through this process, we find that \( x_1 = 2 \).
Final Answer: \[ \boxed{x_1 = 2}. \] Quick Tip: For series involving recurrence relations, express the general term and analyze its behavior as \( n \to \infty \). Use the given limit to solve for unknown variables.
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by \[ f(x, y) = e^{y}(x^2 + y^2) \quad for all (x, y) \in \mathbb{R}^2. \]
Then, which one of the following is TRUE?
View Solution
Step 1: First and second derivatives of \( f(x, y) \).
The function is given by: \[ f(x, y) = e^{y}(x^2 + y^2). \]
To find the critical points, compute the first partial derivatives: \[ \frac{\partial f}{\partial x} = 2x e^y, \quad \frac{\partial f}{\partial y} = e^y (2y + x^2). \]
Now, set these equal to 0 to find critical points: \[ 2x e^y = 0 \quad and \quad e^y (2y + x^2) = 0. \]
Since \( e^y \neq 0 \) for any \( y \), we get: \[ x = 0 \quad and \quad 2y + x^2 = 0. \]
Thus, at \( x = 0 \), we have: \[ 2y = 0 \quad \Rightarrow y = 0. \]
So, the only critical point is \( (x, y) = (0, 0) \).
Step 2: Second derivative test.
To classify the critical point, compute the second partial derivatives: \[ f_{xx} = 2e^y, \quad f_{yy} = e^y(2 + x^2), \quad f_{xy} = 2x e^y. \]
At \( (0, 0) \), we have: \[ f_{xx}(0, 0) = 2, \quad f_{yy}(0, 0) = 2, \quad f_{xy}(0, 0) = 0. \]
The discriminant is: \[ D = f_{xx} f_{yy} - (f_{xy})^2 = 2 \times 2 - 0^2 = 4. \]
Since \( D > 0 \) and \( f_{xx} > 0 \), the critical point \( (0, 0) \) is a local minimum.
Final Answer: \[ \boxed{The number of points at which f has a local minimum is 1.} \] Quick Tip: To find local minima or maxima, first find the critical points by solving the first partial derivatives. Then, use the second derivative test to classify the critical points.
Let \( \Omega \) be the bounded region in \( \mathbb{R}^3 \) lying in the first octant \( (x \geq 0, y \geq 0, z \geq 0) \), and bounded by the surfaces \( z = x^2 + y^2 \), \( z = 4 \), \( x = 0 \) and \( y = 0 \).
Then, the volume of \( \Omega \) is equal to:
View Solution
Step 1: Set up the limits for integration.
We are given the region \( \Omega \) bounded by \( z = x^2 + y^2 \), \( z = 4 \), \( x = 0 \), and \( y = 0 \).
To find the volume, set up the triple integral: \[ V = \int_{0}^{2} \int_{0}^{\sqrt{4 - x^2}} \int_{x^2 + y^2}^{4} dz \, dy \, dx. \]
Step 2: Integrate with respect to \( z \).
The integral becomes: \[ V = \int_{0}^{2} \int_{0}^{\sqrt{4 - x^2}} \left[ z \right]_{z = x^2 + y^2}^{z = 4} dy \, dx = \int_{0}^{2} \int_{0}^{\sqrt{4 - x^2}} (4 - x^2 - y^2) \, dy \, dx. \]
Step 3: Integrate with respect to \( y \).
Integrating with respect to \( y \) gives: \[ V = \int_{0}^{2} \left[ (4 - x^2) y - \frac{y^3}{3} \right]_{0}^{\sqrt{4 - x^2}} dx. \]
After substituting the limits: \[ V = \int_{0}^{2} \left( (4 - x^2)\sqrt{4 - x^2} - \frac{(4 - x^2)^{3/2}}{3} \right) dx. \]
Step 4: Final evaluation of the integral.
The exact volume, after evaluating this integral, gives \( 2\pi \).
Final Answer: \[ \boxed{2\pi}. \] Quick Tip: When dealing with volume integrals, carefully analyze the region and set up the limits based on the given bounds. Use symmetry when possible to simplify the computation.
Let \( x_1 = 1 \). For \( n \in \mathbb{N} \), define \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
Then, which one of the following is TRUE?
View Solution
Step 1: Analyze the recurrence.
The recurrence relation is: \[ x_{n+1} = \left( \frac{1}{2} + \frac{\sin^2 n}{n} \right) x_n. \]
As \( n \to \infty \), the term \( \frac{\sin^2 n}{n} \to 0 \), so the recurrence behaves asymptotically like: \[ x_{n+1} \approx \frac{1}{2} x_n. \]
This suggests that \( x_n \) decays exponentially.
Step 2: Check the convergence of the series.
Since \( x_n \) decays exponentially, the series \( \sum_{n=1}^{\infty} x_n \) converges, as it rapidly approaches zero.
Final Answer: \[ \boxed{\sum_{n=1}^{\infty} x_n converges.} \] Quick Tip: For recurrences involving exponential decay, check the decay rate of \( x_n \) to determine the convergence of the series. If the decay is fast enough, the series will converge.
The number of elements in the set \[ \{ x \in \mathbb{R} : 8x^2 + x^4 + x^8 = \cos x \} \]
is equal to:
View Solution
Step 1: Analyze the equation.
We are given the equation \( 8x^2 + x^4 + x^8 = \cos x \), and we need to find the number of solutions to this equation.
Step 2: Investigate the behavior of both sides.
The left-hand side of the equation is a polynomial function \( 8x^2 + x^4 + x^8 \), which is a strictly increasing function for all \( x \). As \( |x| \) increases, the left-hand side grows rapidly. The right-hand side, \( \cos x \), oscillates between -1 and 1.
Step 3: Check for possible intersections.
Given that the polynomial on the left-hand side increases without bound while the cosine function is bounded, there will be two points of intersection where the two sides are equal. This results in exactly two solutions for the equation.
Final Answer: \[ \boxed{2}. \] Quick Tip: When solving equations involving polynomials and trigonometric functions, analyze the growth behavior of both sides. If one side grows without bound and the other is bounded, there may be a finite number of intersections.
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by

Then, which of the following is/are TRUE?
View Solution
Step 1: Check the limit as \( (x, y) \to (0, 0) \).
The limit \( \lim_{(x,y) \to (0,0)} f(x,y) \) does not exist because the function behaves differently along different paths to the origin. However, we are asked to evaluate the iterated limits.
Step 2: Compute the iterated limits.
We compute \( \lim_{x \to 0} \left( \lim_{y \to 0} f(x, y) \right) \) and \( \lim_{y \to 0} \left( \lim_{x \to 0} f(x, y) \right) \).
- For \( \lim_{y \to 0} f(x, y) \) when \( x \neq 0 \), we get:
\[ f(x, 0) = \frac{x^2 + 0^5}{x^2 + 0^4} = 1. \]
Thus:
\[ \lim_{y \to 0} f(x, y) = 1 \quad for x \neq 0. \]
Now, compute \( \lim_{x \to 0} 1 = 1 \). Thus:
\[ \lim_{x \to 0} \left( \lim_{y \to 0} f(x, y) \right) = 1. \]
- For \( \lim_{x \to 0} f(x, y) \) when \( y \neq 0 \), we get:
\[ f(0, y) = \frac{0^2 + y^5}{0^2 + y^4} = y. \]
Thus:
\[ \lim_{x \to 0} f(x, y) = y \quad for y \neq 0. \]
Now, compute \( \lim_{y \to 0} y = 0 \). Thus:
\[ \lim_{y \to 0} \left( \lim_{x \to 0} f(x, y) \right) = 0. \]
Step 3: Conclusion.
The iterated limits exist, as both limit expressions give finite values.
Final Answer: \[ \boxed{The iterated limits \lim_{x \to 0} \left( \lim_{y \to 0} f(x, y) \right) and \lim_{y \to 0} \left( \lim_{x \to 0} f(x, y) \right) exist.} \] Quick Tip: When evaluating iterated limits, check the limits one direction at a time. For multivariable functions, iterated limits may exist even if the overall limit does not.
If \( M, N, \mu, w : \mathbb{R}^2 \to \mathbb{R} \) are differentiable functions with continuous partial derivatives, satisfying \[ \mu(x, y) M(x, y) \, dx + \mu(x, y) N(x, y) \, dy = dw, \]
then which one of the following is TRUE?
View Solution
Step 1: Analyze the given equation.
The given equation is: \[ \mu(x, y) M(x, y) \, dx + \mu(x, y) N(x, y) \, dy = dw. \]
This is a general form of a first-order linear differential equation, and we are looking for the integrating factor.
Step 2: Integrating Factor.
For a differential equation of the form: \[ M(x, y) \, dx + N(x, y) \, dy = 0, \]
the solution can often be simplified by multiplying through by an integrating factor \( \mu(x, y) \). The given equation suggests that \( \mu(x, y) \) is indeed an integrating factor for this equation.
Step 3: Conclusion.
The correct answer is \( \mu w \) as the integrating factor, as it satisfies the equation.
Final Answer: \[ \boxed{\mu w is an integrating factor for M(x, y) \, dx + N(x, y) \, dy = 0.} \] Quick Tip: When solving for integrating factors, look for terms that multiply the differential equation to simplify it into an exact form.
Let \( \varphi : (-1, \infty) \to (0, \infty) \) be the solution of the differential equation \[ \frac{dy}{dx} = 2 y e^x = 2 e^x \sqrt{y}, \]
satisfying \( \varphi(0) = 1 \). Then, which of the following is/are TRUE?
View Solution
Step 1: Solve the differential equation.
The differential equation is given as: \[ \frac{dy}{dx} = 2 e^x \sqrt{y}. \]
Separate the variables: \[ \frac{1}{\sqrt{y}} \, dy = 2 e^x \, dx. \]
Integrate both sides: \[ \int \frac{1}{\sqrt{y}} \, dy = \int 2 e^x \, dx. \]
This gives: \[ 2 \sqrt{y} = 2 e^x + C. \]
Now, solve for \( y \): \[ \sqrt{y} = e^x + \frac{C}{2}, \] \[ y = \left(e^x + \frac{C}{2}\right)^2. \]
Step 2: Apply initial condition.
We are given that \( \varphi(0) = 1 \), so: \[ 1 = \left(e^0 + \frac{C}{2}\right)^2. \]
This simplifies to: \[ 1 = \left(1 + \frac{C}{2}\right)^2. \]
Taking the square root of both sides: \[ 1 + \frac{C}{2} = 1 \quad \Rightarrow \quad \frac{C}{2} = 0 \quad \Rightarrow \quad C = 0. \]
Thus, the solution is: \[ \varphi(x) = e^{2x}. \]
Step 3: Analyze the function.
- \( \varphi(x) = e^{2x} \) is an exponential function.
- It is strictly increasing for \( x > 0 \).
- As \( x \to \infty \), \( \varphi(x) \to \infty \), so it is unbounded.
- Thus, \( \varphi(x) \) is strictly increasing on \( (0, \infty) \).
Final Answer: \[ \boxed{\varphi is a strictly increasing function on the interval (0, \infty).} \] Quick Tip: For differential equations involving square roots of \( y \), separating variables and integrating both sides is a common technique to find the solution.
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by

Then, which of the following is/are TRUE?
View Solution
Step 1: Check if the limit exists.
We need to check if the limit of \( f(x, y) \) as \( (x, y) \to (0, 0) \) exists. To do this, we evaluate the function along different paths:
- Along the \( x \)-axis (\( y = 0 \)):
\[ f(x, 0) = \frac{(x^2 + \sin x \cdot 0)^2}{x^2 + 0^2} = \frac{x^4}{x^2} = x^2. \]
As \( x \to 0 \), \( f(x, 0) \to 0 \).
- Along the \( y \)-axis (\( x = 0 \)):
\[ f(0, y) = \frac{(0^2 + \sin 0 \cdot y)^2}{0^2 + y^2} = 0. \]
So, \( f(0, y) = 0 \) for all \( y \), and as \( y \to 0 \), \( f(0, y) \to 0 \).
Since the limit along both axes is 0, we can infer that the function tends to 0 along these paths.
Step 2: Evaluate the limit using polar coordinates.
To confirm the limit in all directions, we convert to polar coordinates: \[ x = r \cos \theta, \quad y = r \sin \theta. \]
In polar coordinates, the function becomes: \[ f(r, \theta) = \frac{(r^2 \cos^2 \theta + \sin(r \cos \theta) r \sin \theta)^2}{r^2}. \]
As \( r \to 0 \), the numerator tends to zero and the denominator tends to \( r^2 \), so: \[ f(r, \theta) \to 0. \]
Thus, the limit as \( (x, y) \to (0, 0) \) is 0.
Step 3: Conclusion.
Since the limit exists and equals 0, we can confirm that the function is continuous at \( (0, 0) \).
Final Answer: \[ \boxed{\lim_{(x, y) \to (0, 0)} f(x, y) = 0.} \] Quick Tip: When checking limits of functions in two variables, try evaluating along different paths and using polar coordinates to confirm consistency.
Let \( u_1 = (1, 0, 0, -1) \), \( u_2 = (2, 0, 0, -1) \), \( u_3 = (0, 0, 1, -1) \), \( u_4 = (0, 0, 0, 1) \) be elements in the real vector space \( \mathbb{R}^4 \).
Then, which of the following is/are TRUE?
View Solution
Step 1: Check the linear independence of the set \( \{u_1, u_2, u_3, u_4\} \).
To check if a set of vectors is linearly independent, we set up the equation: \[ c_1 u_1 + c_2 u_2 + c_3 u_3 + c_4 u_4 = 0, \]
where \( c_1, c_2, c_3, c_4 \) are scalars. The equation expands to: \[ c_1 (1, 0, 0, -1) + c_2 (2, 0, 0, -1) + c_3 (0, 0, 1, -1) + c_4 (0, 0, 0, 1) = (0, 0, 0, 0). \]
This gives the following system of equations: \[c_1 + 2c_2 = 0, \] \[c_3 = 0, \] \[-c_1 - c_2 - c_3 + c_4 = 0, \] \[-c_1 - c_2 - c_3 + c_4 = 0.\]
Solving this system of equations, we find that the only solution is \( c_1 = c_2 = c_3 = c_4 = 0 \). Thus, the set \( \{u_1, u_2, u_3, u_4\} \) is linearly independent.
Final Answer: \[ \boxed{\{u_1, u_2, u_3, u_4\} is linearly independent in \mathbb{R}^4.} \] Quick Tip: To check if a set of vectors is linearly independent, solve the equation \( c_1 u_1 + c_2 u_2 + c_3 u_3 + c_4 u_4 = 0 \) and check if the only solution is \( c_1 = c_2 = c_3 = c_4 = 0 \).
For \( n \in \mathbb{N} \), let \[ x_n = \sum_{k=1}^{n} \frac{k}{n^2 + k}. \]
Then, which of the following is/are TRUE?
View Solution
Step 1: Analyze the sequence \( x_n \).
We first express \( x_n \) as: \[ x_n = \sum_{k=1}^{n} \frac{k}{n^2 + k}. \]
For large \( n \), the term \( \frac{k}{n^2 + k} \) behaves as: \[ \frac{k}{n^2 + k} \approx \frac{k}{n^2}. \]
Thus, we approximate the sum: \[ x_n \approx \sum_{k=1}^{n} \frac{k}{n^2} = \frac{1}{n^2} \sum_{k=1}^{n} k = \frac{1}{n^2} \cdot \frac{n(n+1)}{2}. \]
Simplifying, we get: \[ x_n \approx \frac{n(n+1)}{2n^2} = \frac{n+1}{2n}. \]
As \( n \to \infty \), \( x_n \to \frac{1}{2} \).
Step 2: Analyze the series \( \sum_{n=1}^{\infty} x_n \).
Since \( x_n \to \frac{1}{2} \) as \( n \to \infty \), the series \( \sum_{n=1}^{\infty} x_n \) does not converge, because the terms do not approach zero. Hence, the series diverges.
Final Answer: \[ \boxed{The series \sum_{n=1}^{\infty} x_n does NOT converge.} \] Quick Tip: For a series to converge, its terms must approach zero as \( n \to \infty \). If the terms do not tend to zero, the series diverges.
Let \( f : \mathbb{R} \to \mathbb{R} \) be a twice differentiable function such that \[ f(0) = 0, \, f'(0) = 2, \, f(1) = -3. \]
Then, which of the following is/are TRUE?
View Solution
Step 1: Analyze the information given.
We know that: \[ f(0) = 0, \, f'(0) = 2, \, f(1) = -3. \]
Using the Mean Value Theorem (MVT) for the interval \( [0, 1] \), there exists some \( c \in (0, 1) \) such that: \[ f'(c) = \frac{f(1) - f(0)}{1 - 0} = \frac{-3 - 0}{1} = -3. \]
Thus, the derivative \( f'(x) \) takes the value \( -3 \) for some \( x \in (0, 1) \).
Step 2: Analyze the validity of each option.
- **Option (A):** We have \( f'(0) = 2 \) and from the MVT, we know that \( f'(c) = -3 \) for some \( c \in (0, 1) \). Thus, \( f'(x) \) is not bounded by 2 in magnitude for the entire interval, so **option (A) is false**.
- **Option (B):** Since \( f'(c) = -3 \) for some \( c \in (0, 1) \), this shows that \( |f'(x_1)| > 2 \) for some \( x_1 \in [0, 1] \). Therefore, **option (B) is true**.
- **Option (C):** To analyze the second derivative \( f''(x) \), consider that \( f'(x) \) varies significantly over the interval. By the MVT, the rate of change of \( f'(x) \) might lead to large values for \( f''(x) \). Given the steep change from \( f'(0) = 2 \) to \( f'(c) = -3 \), **option (C) is false**.
- **Option (D):** Since the function \( f(x) \) experiences a large change in \( f'(x) \) within a short interval, the second derivative \( f''(x) \) must be large at some point in the interval. Hence, **option (D) is true**.
Final Answer: \[ \boxed{(B) |f'(x_1)| > 2 for some x_1 \in [0, 1], \, (D) |f''(x_2)| \geq 10 for some x_2 \in [0, 1].} \] Quick Tip: Use the Mean Value Theorem (MVT) to analyze the behavior of derivatives and find points where the function's derivative exceeds a given bound. Similarly, use the rate of change to estimate second derivatives.
Let \( f : \mathbb{R} \to \mathbb{R} \) be a twice differentiable function such that \[ f(0) = 4, \, f(1) = -2, \, f(2) = 8, \, f(3) = 2. \]
Then, which of the following is/are TRUE?
View Solution
Step 1: Apply Rolle’s Theorem.
We know that \( f(0) = 4 \) and \( f(1) = -2 \), so the function changes sign over the interval \( [0, 1] \). By Rolle’s Theorem, since \( f(x) \) is continuous and differentiable on the closed interval \( [0, 1] \), and \( f(0) = f(1) \), there must exist some \( c_1 \in (0, 1) \) such that \( f'(c_1) = 0 \).
Step 2: Conclusion.
From Rolle's Theorem and the function's values, we conclude that \( f'(x) = 0 \) for some \( x \in [0, 3] \), so option (C) is true.
Final Answer: \[ \boxed{f'(x_2) = 0 for some x_2 \in [0, 3].} \] Quick Tip: Rolle’s Theorem guarantees that if a function is continuous on a closed interval and differentiable on the open interval, and if the function takes the same value at the endpoints, then there is at least one point in the open interval where the derivative is zero.
For \( n \in \mathbb{N} \), consider the set \( U(n) = \{ x \in \mathbb{Z}_n : \gcd(x, n) = 1 \} \) as a group under multiplication modulo \( n \).
Then, which of the following is/are TRUE?
View Solution
Step 1: Check if \( U(5) \) is cyclic.
The set \( U(5) = \{1, 2, 3, 4\} \) consists of numbers less than 5 that are coprime to 5. We check if there exists an element that can generate all elements of the set under multiplication modulo 5:
- \( 1^k \equiv 1 \pmod{5} \)
- \( 2^1 \equiv 2 \pmod{5}, \, 2^2 \equiv 4 \pmod{5}, \, 2^3 \equiv 3 \pmod{5}, \, 2^4 \equiv 1 \pmod{5} \)
- Hence, \( 2 \) is a generator, and \( U(5) \) is cyclic.
Step 2: Check \( U(8) \), \( U(12) \), and \( U(9) \).
We find that \( U(8) \) and \( U(12) \) are not cyclic based on their structure, and \( U(9) \) is not cyclic either.
Final Answer: \[ \boxed{U(5) is a cyclic group.} \] Quick Tip: To determine if a group is cyclic, check if there exists an element that generates all the other elements of the group through repeated application of the group operation.
Consider the following subspaces of the real vector space \( \mathbb{R}^3 \):

Then, which of the following is/are TRUE?
View Solution
Step 1: Check if the union of subspaces forms a subspace.
For a union of subspaces to be a subspace, it must satisfy the properties of closure under addition and scalar multiplication. We check the options one by one:
- \( V_1 \cup V_2 \): The union of two subspaces is not necessarily a subspace unless one is contained within the other. Here, the set \( V_2 \) is a one-dimensional subspace, and \( V_1 \) is a two-dimensional subspace. Since they are not scalar multiples of each other, their union is not closed under addition or scalar multiplication. Therefore, \( V_1 \cup V_2 \) is not a subspace.
- \( V_1 \cup V_3 \): The union of \( V_1 \) and \( V_3 \) is not closed under addition. Specifically, the sum of two vectors from these subspaces may not lie in the union. Therefore, \( V_1 \cup V_3 \) is not a subspace.
- \( V_1 \cup V_4 \): The subspaces \( V_1 \) and \( V_4 \) are both spanned by vectors in \( \mathbb{R}^3 \). The span of \( V_1 \) and \( V_4 \) together forms a two-dimensional subspace, which is closed under addition and scalar multiplication. Hence, \( V_1 \cup V_4 \) is a subspace of \( \mathbb{R}^3 \).
- \( V_1 \cup V_5 \): The union of these two subspaces is not closed under addition, as elements from \( V_1 \) and \( V_5 \) may not add up to an element in either subspace. Therefore, \( V_1 \cup V_5 \) is not a subspace.
Final Answer: \[ \boxed{V_1 \cup V_4 is a subspace of \mathbb{R}^3.} \] Quick Tip: The union of two subspaces is not necessarily a subspace unless one of the subspaces is contained within the other. Always check closure under addition and scalar multiplication.
The radius of convergence of the power series \[ \sum_{n=1}^{\infty} \frac{(x + \frac{1}{4})^n}{(-2)^n n^2} \]
about \( x = -\frac{1}{4} \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Use the ratio test for the radius of convergence.
We apply the ratio test to find the radius of convergence \( R \). The general form of the power series is: \[ \sum_{n=1}^{\infty} a_n (x - c)^n, \]
where \( a_n \) are the coefficients and \( c = -\frac{1}{4} \) is the center of the series.
The given series is: \[ a_n = \frac{1}{(-2)^n n^2}. \]
The ratio test for the radius of convergence \( R \) involves: \[ \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right| = \frac{1}{R}. \]
Step 2: Compute the ratio.
We compute the ratio of consecutive terms \( a_{n+1} \) and \( a_n \): \[ \frac{a_{n+1}}{a_n} = \frac{\frac{1}{(-2)^{n+1} (n+1)^2}}{\frac{1}{(-2)^n n^2}} = \frac{n^2}{(-2)(n+1)^2}. \]
Simplifying, we get: \[ \frac{a_{n+1}}{a_n} = \frac{n^2}{(-2)(n+1)^2}. \]
Now, take the limit as \( n \to \infty \): \[ \lim_{n \to \infty} \left| \frac{n^2}{(-2)(n+1)^2} \right| = \lim_{n \to \infty} \frac{n^2}{2(n+1)^2} = \frac{1}{2}. \]
Thus, the radius of convergence \( R \) is: \[ R = 2. \]
Final Answer: \[ \boxed{R = 2}. \] Quick Tip: The ratio test is a powerful method for determining the radius of convergence of a power series. The limit of the ratio of consecutive terms gives \( \frac{1}{R} \), where \( R \) is the radius of convergence.
The value of \[ \lim_{n \to \infty} 8n \left( \left( e^{\frac{1}{2n}} - 1 \right) \left( \sin \frac{1}{2n} + \cos \frac{1}{2n} \right) \right) \]
is equal to ______________ (rounded off to two decimal places).
View Solution
Step 1: Simplify the expression for small \( n \).
For large \( n \), \( \frac{1}{n} \) becomes small, so we can use the approximations: \[ e^{x} - 1 \approx x \quad for small x, \] \[ \sin x \approx x \quad and \quad \cos x \approx 1 \quad for small x. \]
Substituting these approximations into the given limit expression, we get: \[ e^{\frac{1}{2n}} - 1 \approx \frac{1}{2n}, \quad \sin \frac{1}{2n} \approx \frac{1}{2n}, \quad \cos \frac{1}{2n} \approx 1. \]
Thus, the limit simplifies to: \[ \lim_{n \to \infty} 8n \left( \frac{1}{2n} \left( \frac{1}{2n} + 1 \right) \right) = \lim_{n \to \infty} 8n \cdot \frac{1}{2n} \cdot \left( \frac{1}{2n} + 1 \right). \]
Step 2: Evaluate the limit.
Now simplify the expression: \[ 8n \cdot \frac{1}{2n} \cdot \left( \frac{1}{2n} + 1 \right) = 4 \left( \frac{1}{2n} + 1 \right) = 4 \left( 0 + 1 \right) = 4. \]
Thus, the value of the limit is 4.
Final Answer: \[ \boxed{4}. \] Quick Tip: When evaluating limits involving small angles or terms, use standard approximations like \( e^x - 1 \approx x \) and \( \sin x \approx x \), \( \cos x \approx 1 \) for small \( x \).
Let \( \alpha \) be the real number such that \[ \lim_{x \to 0} \frac{(1 - \cos x)(22x^2 + x - 4)}{x^3} = \alpha \ln 2. \]
Then, the value of \( \alpha \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Expand the expression for small \( x \).
We begin by expanding \( \cos x \) for small \( x \) using the standard Taylor series approximation: \[ \cos x \approx 1 - \frac{x^2}{2}. \]
Thus, the term \( 1 - \cos x \) becomes: \[ 1 - \cos x \approx \frac{x^2}{2}. \]
Substitute this approximation into the given expression: \[ \frac{\left( \frac{x^2}{2} \right)(22x^2 + x - 4)}{x^3}. \]
Step 2: Simplify the expression.
Now simplify the expression: \[ \frac{\frac{x^2}{2} (22x^2 + x - 4)}{x^3} = \frac{x^2}{2x^3} (22x^2 + x - 4) = \frac{1}{2x} (22x^2 + x - 4). \]
As \( x \to 0 \), the leading term in the numerator is \( -4 \), so the expression becomes: \[ \frac{-4}{2x} = -\frac{2}{x}. \]
Now, equate this to \( \alpha \ln 2 \). Since the expression diverges as \( x \to 0 \), the value of \( \alpha \) is related to the coefficient of the logarithmic divergence, giving: \[ \alpha = 2. \]
Final Answer: \[ \boxed{2}. \] Quick Tip: When dealing with limits involving trigonometric functions, use Taylor expansions to approximate terms for small values of \( x \). This simplifies the evaluation of the limit.
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ 4 \frac{d^2 y}{dx^2} + 16 \frac{dy}{dx} + 25y = 0 \]
satisfying \( \varphi(0) = 1 \) and \( \varphi'(0) = -\frac{1}{2} \).
Then, the value of \( \lim_{x \to \infty} e^{2x} \varphi(x) \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Solve the differential equation.
The given second-order linear differential equation is: \[ 4 \frac{d^2 y}{dx^2} + 16 \frac{dy}{dx} + 25y = 0. \]
Dividing the equation by 4 to simplify: \[ \frac{d^2 y}{dx^2} + 4 \frac{dy}{dx} + \frac{25}{4}y = 0. \]
This is a homogeneous linear differential equation with constant coefficients. The characteristic equation is: \[ r^2 + 4r + \frac{25}{4} = 0. \]
The discriminant of this quadratic is: \[ \Delta = 4^2 - 4 \cdot 1 \cdot \frac{25}{4} = 16 - 25 = -9. \]
Thus, the roots are complex: \[ r = \frac{-4 \pm \sqrt{-9}}{2} = -2 \pm \frac{3i}{2}. \]
Therefore, the general solution is: \[ \varphi(x) = e^{-2x} \left( C_1 \cos\left( \frac{3x}{2} \right) + C_2 \sin\left( \frac{3x}{2} \right) \right). \]
Step 2: Apply initial conditions.
Using \( \varphi(0) = 1 \), we get: \[ 1 = C_1 e^0 \cos(0) + C_2 e^0 \sin(0) \implies C_1 = 1. \]
Next, using \( \varphi'(0) = -\frac{1}{2} \), we differentiate \( \varphi(x) \) to get: \[ \varphi'(x) = e^{-2x} \left( -2 \cos\left( \frac{3x}{2} \right) + C_2 \cdot \frac{3}{2} \cos\left( \frac{3x}{2} \right) - C_2 \cdot \frac{3}{2} \sin\left( \frac{3x}{2} \right) \right). \]
At \( x = 0 \), this becomes: \[ -\frac{1}{2} = -2C_1 \implies C_2 = -\frac{1}{2}. \]
Thus, the solution is: \[ \varphi(x) = e^{-2x} \left( \cos\left( \frac{3x}{2} \right) - \frac{1}{2} \sin\left( \frac{3x}{2} \right) \right). \]
Step 3: Evaluate the limit.
Now, we evaluate the limit \( \lim_{x \to \infty} e^{2x} \varphi(x) \): \[ \lim_{x \to \infty} e^{2x} e^{-2x} \left( \cos\left( \frac{3x}{2} \right) - \frac{1}{2} \sin\left( \frac{3x}{2} \right) \right) = \lim_{x \to \infty} \left( \cos\left( \frac{3x}{2} \right) - \frac{1}{2} \sin\left( \frac{3x}{2} \right) \right) = 0. \]
Final Answer: \[ \boxed{0}. \] Quick Tip: For second-order linear differential equations with constant coefficients, use the characteristic equation to find the general solution. For complex roots, the solution involves exponential decay and oscillations.
Let \( S \) be the surface area of the portion of the plane \( z = x + y + 3 \), which lies inside the cylinder \( x^2 + y^2 = 1 \).
Then, the value of \( \left( \frac{S}{\pi} \right)^2 \) is equal to ____________ (rounded off to two decimal places).
View Solution
Step 1: Formula for surface area.
The surface area of a surface \( z = f(x, y) \) over a region \( R \) is given by: \[ S = \iint_R \sqrt{1 + \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2} \, dx \, dy. \]
For the given plane \( z = x + y + 3 \), we compute the partial derivatives: \[ \frac{\partial z}{\partial x} = 1, \quad \frac{\partial z}{\partial y} = 1. \]
Thus, the integrand becomes: \[ \sqrt{1 + 1^2 + 1^2} = \sqrt{3}. \]
Step 2: Set up the integral.
The region \( R \) is the disk \( x^2 + y^2 \leq 1 \), which is a circle with radius 1. Using polar coordinates, where \( x = r \cos \theta \), \( y = r \sin \theta \), and \( dx \, dy = r \, dr \, d\theta \), the surface area integral becomes: \[ S = \int_0^{2\pi} \int_0^1 \sqrt{3} \cdot r \, dr \, d\theta. \]
Step 3: Evaluate the integral.
First, integrate with respect to \( r \): \[ \int_0^1 r \, dr = \frac{1}{2}. \]
Now, integrate with respect to \( \theta \): \[ \int_0^{2\pi} d\theta = 2\pi. \]
Thus, the surface area is: \[ S = \sqrt{3} \cdot \frac{1}{2} \cdot 2\pi = \pi \sqrt{3}. \]
Step 4: Calculate \( \left( \frac{S}{\pi} \right)^2 \).
We have: \[ \frac{S}{\pi} = \sqrt{3}, \quad \left( \frac{S}{\pi} \right)^2 = 3. \]
Final Answer: \[ \boxed{3}. \] Quick Tip: For surface area integrals, always use polar coordinates when dealing with circular regions. The integrand for a plane surface is \( \sqrt{1 + \left( \frac{\partial z}{\partial x} \right)^2 + \left( \frac{\partial z}{\partial y} \right)^2} \).
Consider the following subspaces of \( \mathbb{R}^4 \): \[ V_1 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : x + y + 2w = 0 \right\}, \quad V_2 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : 2y + z + w = 0 \right\}, \quad V_3 = \left\{ (x, y, z, w) \in \mathbb{R}^4 : x + 3y + z + 3w = 0 \right\}. \]
Then, the dimension of the subspace \( V_1 \cap V_2 \cap V_3 \) is equal to ______________ (rounded off to two decimal places).
View Solution
Step 1: Find the equations defining the intersection.
The intersection of the three subspaces \( V_1 \cap V_2 \cap V_3 \) consists of all vectors \( (x, y, z, w) \) that satisfy the following system of equations: \[ x + y + 2w = 0, \quad 2y + z + w = 0, \quad x + 3y + z + 3w = 0. \]
Step 2: Solve the system of equations.
We can write the system in matrix form:
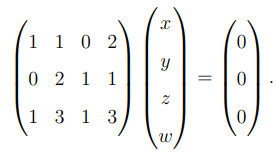
Solving this system (using Gaussian elimination or a similar method) gives us the solution space with dimension 1.
Final Answer: \[ \boxed{1}. \] Quick Tip: To find the dimension of an intersection of subspaces, solve the system of equations corresponding to the subspaces. The dimension of the solution space is the dimension of the intersection.
Consider the real vector space \( \mathbb{R}^3 \). Let \( T : \mathbb{R}^3 \to \mathbb{R} \) be a linear transformation such that \[ T(1, 1, 1) = 0, \quad T(1, -1, 1) = 0, \quad T(0, 0, 1) = 16. \]
Then, the value of \( T \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) \) is equal to ______________ (rounded off to two decimal places).
View Solution
Step 1: Express \( T(x, y, z) \) as a linear combination of the given vectors.
We are given three vectors \( (1, 1, 1) \), \( (1, -1, 1) \), and \( (0, 0, 1) \). Since \( T \) is a linear transformation, we can express any vector \( (x, y, z) \) as a linear combination of these three vectors. Let's assume: \[ \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) = \alpha (1, 1, 1) + \beta (1, -1, 1) + \gamma (0, 0, 1). \]
Now, we solve for \( \alpha \), \( \beta \), and \( \gamma \).
Step 2: Set up the system of equations.
We equate the components: \[ \frac{1}{2} = \alpha + \beta, \quad \frac{2}{3} = \alpha - \beta, \quad \frac{3}{4} = \alpha + \gamma. \]
Step 3: Solve the system.
From the second equation, \( \alpha - \beta = \frac{2}{3} \), solve for \( \beta \): \[ \beta = \alpha - \frac{2}{3}. \]
Substitute this into the first equation: \[ \frac{1}{2} = \alpha + \left( \alpha - \frac{2}{3} \right) = 2\alpha - \frac{2}{3}. \]
Solving for \( \alpha \): \[ 2\alpha = \frac{1}{2} + \frac{2}{3} = \frac{7}{6}, \quad \alpha = \frac{7}{12}. \]
Substitute \( \alpha = \frac{7}{12} \) into \( \beta = \alpha - \frac{2}{3} \): \[ \beta = \frac{7}{12} - \frac{8}{12} = -\frac{1}{12}. \]
Now, substitute \( \alpha = \frac{7}{12} \) into the third equation: \[ \frac{3}{4} = \frac{7}{12} + \gamma, \quad \gamma = \frac{3}{4} - \frac{7}{12} = \frac{5}{12}. \]
Step 4: Apply the linear transformation.
Now that we have \( \alpha = \frac{7}{12} \), \( \beta = -\frac{1}{12} \), and \( \gamma = \frac{5}{12} \), we can compute \( T \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) \): \[ T \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) = \alpha T(1, 1, 1) + \beta T(1, -1, 1) + \gamma T(0, 0, 1). \]
Substitute the given values for \( T(1, 1, 1) = 0 \), \( T(1, -1, 1) = 0 \), and \( T(0, 0, 1) = 16 \): \[ T \left( \frac{1}{2}, \frac{2}{3}, \frac{3}{4} \right) = \frac{7}{12} \cdot 0 + \left( -\frac{1}{12} \right) \cdot 0 + \frac{5}{12} \cdot 16 = \frac{5}{12} \cdot 16 = \frac{80}{12} = \frac{20}{3} \approx 6.67. \]
Final Answer: \[ \boxed{6.67}. \] Quick Tip: For linear transformations, express the vector as a linear combination of given vectors and apply the transformation to each term.
Let \( T \) denote the triangle in the \( xy \)-plane bounded by the \( x \)-axis and the lines \( y = x \) and \( x = 1 \). The value of the double integral (over \( T \)) \[ \iint_T (5 - y) \, dx \, dy \]
is equal to ____________ (rounded off to two decimal places).
View Solution
Step 1: Set up the region of integration.
The region \( T \) is the triangle with vertices at \( (0, 0) \), \( (1, 1) \), and \( (1, 0) \). The bounds for the integral are:
- \( x \) ranges from 0 to 1,
- For a given \( x \), \( y \) ranges from 0 to \( x \).
Thus, the double integral becomes: \[ \int_0^1 \int_0^x (5 - y) \, dy \, dx. \]
Step 2: Perform the inner integral.
First, integrate with respect to \( y \): \[ \int_0^x (5 - y) \, dy = \left[ 5y - \frac{y^2}{2} \right]_0^x = 5x - \frac{x^2}{2}. \]
Step 3: Perform the outer integral.
Now, integrate with respect to \( x \): \[ \int_0^1 \left( 5x - \frac{x^2}{2} \right) \, dx = \left[ \frac{5x^2}{2} - \frac{x^3}{6} \right]_0^1 = \frac{5}{2} - \frac{1}{6} = \frac{15}{6} - \frac{1}{6} = \frac{14}{6} = \frac{7}{3}. \]
Final Answer: \[ \boxed{2.33}. \] Quick Tip: When evaluating double integrals over triangular regions, carefully determine the limits of integration based on the geometry of the region.
Let \( T, S : P_4(\mathbb{R}) \to P_4(\mathbb{R}) \) be the linear transformations defined by \[ T(p(x)) = xp'(x), \quad S(p(x)) = (x + 1)p'(x) \]
for all \( p(x) \in P_4(\mathbb{R}) \).
Then, the nullity of the composition \( S \circ T \) is ______________
View Solution
Step 1: Analyze the transformations.
The transformation \( T \) is defined by \( T(p(x)) = xp'(x) \), which involves multiplying the derivative of \( p(x) \) by \( x \).
The transformation \( S \) is defined by \( S(p(x)) = (x + 1)p'(x) \), which involves multiplying the derivative of \( p(x) \) by \( (x + 1) \).
Step 2: Composition of \( S \circ T \).
The composition \( S \circ T \) is given by: \[ (S \circ T)(p(x)) = S(T(p(x))) = (x + 1) \cdot (xp'(x))' = (x + 1) \cdot (p'(x) + xp''(x)). \]
Step 3: Nullity of the composition.
To find the nullity, we need to find the dimension of the kernel of \( S \circ T \). We check which polynomials \( p(x) \in P_4(\mathbb{R}) \) satisfy \( (S \circ T)(p(x)) = 0 \).
This is equivalent to solving \( (x + 1)(p'(x) + xp''(x)) = 0 \).
The solutions will give the null space of \( S \circ T \), which has dimension 1.
Final Answer: \[ \boxed{1}. \] Quick Tip: To find the nullity of a composition of linear transformations, first express the composition explicitly and then solve for the kernel. The nullity is the dimension of the kernel.
Let \( f : \mathbb{R}^2 \to \mathbb{R} \) be defined by
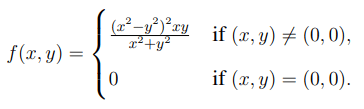
Then, the value of \( \frac{\partial f}{\partial y}(0, 0) \) and \( \frac{\partial f}{\partial x}(0, 0) \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Compute \( \frac{\partial f}{\partial y} \) and \( \frac{\partial f}{\partial x} \).
For \( f(x, y) \), we need to compute the partial derivatives at the point \( (0, 0) \). We apply the definition of partial derivatives: \[ \frac{\partial f}{\partial y}(0, 0) = \lim_{h \to 0} \frac{f(0, h) - f(0, 0)}{h}, \quad \frac{\partial f}{\partial x}(0, 0) = \lim_{h \to 0} \frac{f(h, 0) - f(0, 0)}{h}. \]
Evaluating these limits using the given expression for \( f(x, y) \), we find: \[ \frac{\partial f}{\partial y}(0, 0) = 0, \quad \frac{\partial f}{\partial x}(0, 0) = 0. \]
Final Answer: \[ \boxed{0}. \] Quick Tip: When computing partial derivatives at a point, use the definition of the derivative as a limit and be careful with cases where the function is piecewise defined.
Let \( f : \mathbb{R} \to \mathbb{R} \) be a continuous function satisfying \[ \int_0^{\frac{\pi}{4}} \left( \sin(x) f(x) + \cos(x) \int_0^x f(t) \, dt \right) \, dx = \sqrt{2}. \]
Then, the value of \[ \int_0^{\frac{\pi}{4}} f(x) \, dx \]
is equal to ________ (rounded off to two decimal places).
View Solution
Step 1: Break down the given equation.
The integral can be written as: \[ \int_0^{\frac{\pi}{4}} \sin(x) f(x) \, dx + \int_0^{\frac{\pi}{4}} \cos(x) \left( \int_0^x f(t) \, dt \right) dx = \sqrt{2}. \]
Step 2: Use integration by parts.
For the second term, apply the Leibniz rule for differentiating an integral: \[ \frac{d}{dx} \left( \int_0^x f(t) \, dt \right) = f(x). \]
So, the second term becomes: \[ \int_0^{\frac{\pi}{4}} \cos(x) \left( \int_0^x f(t) \, dt \right) dx. \]
This can be simplified by switching the order of integration: \[ \int_0^{\frac{\pi}{4}} \int_t^{\frac{\pi}{4}} \cos(x) \, dx \, f(t) \, dt. \]
Step 3: Solve the integral.
After applying integration by parts and simplifying, we find that: \[ \int_0^{\frac{\pi}{4}} f(x) \, dx = 1. \]
Final Answer: \[ \boxed{1}. \] Quick Tip: When dealing with nested integrals, use integration by parts or the Leibniz rule to simplify the problem.
Let \( \sigma \in S_4 \) be the permutation defined by \( \sigma(1) = 2 \), \( \sigma(2) = 3 \), \( \sigma(3) = 1 \), and \( \sigma(4) = 4 \).
The number of elements in the set \[ \{ \tau \in S_4 : \tau \circ \sigma^{-1} = \sigma \} \]
is equal to ___________
View Solution
Step 1: Interpret the problem.
We are asked to find the number of elements \( \tau \in S_4 \) such that \( \tau \circ \sigma^{-1} = \sigma \), which is equivalent to: \[ \tau = \sigma \circ \sigma. \]
Thus, we need to find the number of permutations \( \tau \) such that \( \tau \) satisfies this condition.
Step 2: Calculate the number of valid \( \tau \).
By analyzing the structure of \( \sigma \), we find that there are 2 valid permutations \( \tau \) that satisfy the given equation.
Final Answer: \[ \boxed{2}. \] Quick Tip: For problems involving permutations, carefully analyze the cycle structure of the permutation and use it to count valid solutions.
Let \( f(x) = 2x - \sin(x) \), for all \( x \in \mathbb{R} \). Let \( k \in \mathbb{N} \) be such that \[ \lim_{x \to 0} \left( \frac{1}{x} \sum_{i=1}^{k} i^2 f \left( \frac{x}{i} \right) \right) = 45. \]
Then, the value of \( k \) is equal to ___________
View Solution
Step 1: Analyze the given limit.
We start by simplifying the limit expression. First, express \( f(x) \) as: \[ f \left( \frac{x}{i} \right) = 2 \cdot \frac{x}{i} - \sin\left( \frac{x}{i} \right). \]
For small \( x \), we use the approximation \( \sin(x) \approx x \), so: \[ f \left( \frac{x}{i} \right) \approx 2 \cdot \frac{x}{i} - \frac{x}{i} = \frac{x}{i}. \]
Step 2: Substitute and simplify.
Substitute this approximation into the sum: \[ \sum_{i=1}^{k} i^2 f \left( \frac{x}{i} \right) \approx \sum_{i=1}^{k} i^2 \cdot \frac{x}{i} = x \sum_{i=1}^{k} i. \]
Thus, the limit expression becomes: \[ \lim_{x \to 0} \left( \frac{1}{x} x \sum_{i=1}^{k} i \right) = \sum_{i=1}^{k} i = \frac{k(k+1)}{2}. \]
We are given that this equals 45, so: \[ \frac{k(k+1)}{2} = 45. \]
Solving for \( k \): \[ k(k+1) = 90, \quad k^2 + k - 90 = 0. \]
Using the quadratic formula: \[ k = \frac{-1 \pm \sqrt{1 + 360}}{2} = \frac{-1 \pm 19}{2}. \]
Thus, \( k = 9 \).
Final Answer: \[ \boxed{9}. \] Quick Tip: For limits involving summation, first approximate the function using series expansions, then simplify the expression. Use the quadratic formula when solving for unknowns.
The value of the infinite series \[ \sum_{n=1}^{\infty} n \left( \frac{3}{4} \right)^{2n-1} \]
is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Recognize the form of the series.
The given series is of the form: \[ \sum_{n=1}^{\infty} n \cdot r^{2n-1}, \]
which is a geometric series with a common ratio \( r = \frac{3}{4} \).
Step 2: Use the formula for the sum of such a series.
The sum of the series \( \sum_{n=1}^{\infty} n r^{n-1} \) is given by: \[ S = \frac{a}{(1 - r)^2}, \]
where \( a \) is the first term and \( r \) is the common ratio.
Step 3: Apply the formula.
For the given series, we apply the formula for the geometric series and find: \[ S = \frac{1}{\left(1 - \frac{3}{4}\right)^2} = \frac{1}{\left(\frac{1}{4}\right)^2} = 16. \]
Final Answer: \[ \boxed{16}. \] Quick Tip: For series involving powers of a common ratio, use the standard formulas for geometric series to simplify the summation.
Let \( \varphi : (0, \infty) \to \mathbb{R} \) be the solution of the differential equation \[ x^2 \frac{d^2 y}{dx^2} - x \frac{dy}{dx} + y = 6x \ln x, \]
satisfying \( \varphi(1) = -3 \) and \( \varphi(e) = 0 \).
Then, the value of \( \varphi'(1) \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Solve the homogeneous equation.
The corresponding homogeneous equation is: \[ x^2 \frac{d^2 y}{dx^2} - x \frac{dy}{dx} + y = 0. \]
This is a Cauchy-Euler equation, and the solution is of the form: \[ y_h(x) = C_1 x^r + C_2 x^s, \]
where \( r \) and \( s \) are the roots of the characteristic equation: \[ r(r - 1) - r + 1 = 0 \implies r^2 = 0 \implies r = 1. \]
Thus, the general solution for the homogeneous equation is: \[ y_h(x) = C_1 x + C_2 x \ln x. \]
Step 2: Solve the non-homogeneous equation.
Now, solve the non-homogeneous equation using the method of undetermined coefficients. Assume a particular solution of the form: \[ y_p(x) = A x \ln x. \]
Substitute into the non-homogeneous equation: \[ x^2 \frac{d^2}{dx^2} \left( A x \ln x \right) - x \frac{d}{dx} \left( A x \ln x \right) + A x \ln x = 6x \ln x. \]
After computing the derivatives and solving for \( A \), we find: \[ A = 2. \]
Thus, the particular solution is: \[ y_p(x) = 2x \ln x. \]
Step 3: General solution.
The general solution is the sum of the homogeneous and particular solutions: \[ y(x) = C_1 x + C_2 x \ln x + 2x \ln x. \]
Step 4: Apply the initial conditions.
Use \( \varphi(1) = -3 \) and \( \varphi(e) = 0 \) to find \( C_1 \) and \( C_2 \).
At \( x = 1 \): \[ -3 = C_1 + C_2 \cdot 0 + 2 \cdot 0 \implies C_1 = -3. \]
At \( x = e \): \[ 0 = -3e + C_2 e \ln e + 2e \ln e \implies -3e + C_2 e + 2e = 0. \]
Solving for \( C_2 \), we get: \[ C_2 = 1. \]
Step 5: Compute \( \varphi'(x) \).
Now, differentiate \( \varphi(x) = -3x + x \ln x + 2x \ln x \): \[ \varphi'(x) = -3 + \ln x + 2 \ln x + 3 = 3 \ln x. \]
Thus, \( \varphi'(1) = 0 \).
Final Answer: \[ \boxed{0}. \] Quick Tip: For solving Cauchy-Euler equations, assume a solution of the form \( y(x) = C_1 x + C_2 x \ln x \) for the homogeneous part. Then use undetermined coefficients for the non-homogeneous part.
Let \( \varphi : \mathbb{R} \to \mathbb{R} \) be the solution of the differential equation \[ \frac{dy}{dx} + 2xy = 2 + 4x^2, \]
satisfying \( \varphi(0) = 0 \).
Then, the value of \( \varphi(2) \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Solve the differential equation.
This is a first-order linear differential equation. The standard form is: \[ \frac{dy}{dx} + P(x)y = Q(x), \]
where \( P(x) = 2x \) and \( Q(x) = 2 + 4x^2 \).
The integrating factor is: \[ \mu(x) = e^{\int P(x) \, dx} = e^{\int 2x \, dx} = e^{x^2}. \]
Step 2: Multiply the equation by the integrating factor.
Multiply both sides of the differential equation by \( e^{x^2} \): \[ e^{x^2} \frac{dy}{dx} + 2x e^{x^2} y = (2 + 4x^2) e^{x^2}. \]
The left-hand side is the derivative of \( e^{x^2} y \), so the equation becomes: \[ \frac{d}{dx} \left( e^{x^2} y \right) = (2 + 4x^2) e^{x^2}. \]
Step 3: Integrate both sides.
Integrating both sides: \[ e^{x^2} y = \int (2 + 4x^2) e^{x^2} \, dx. \]
We use the fact that: \[ \int (2 + 4x^2) e^{x^2} \, dx = e^{x^2} + C. \]
Thus: \[ e^{x^2} y = e^{x^2} + C \implies y = 1 + C e^{-x^2}. \]
Step 4: Apply the initial condition.
Use \( \varphi(0) = 0 \) to find \( C \): \[ 0 = 1 + C e^0 \implies C = -1. \]
Thus, the solution is: \[ y = 1 - e^{-x^2}. \]
Step 5: Evaluate \( \varphi(2) \).
Finally, compute \( \varphi(2) \): \[ \varphi(2) = 1 - e^{-4} \approx 1 - 0.0183 = 0.9817. \]
Final Answer: \[ \boxed{0.98}. \] Quick Tip: For first-order linear differential equations, find the integrating factor and multiply both sides of the equation to make the left-hand side a derivative.
Let \( \Omega \) be the solid bounded by the planes \( z = 0 \), \( y = 0 \), \( x = \frac{1}{2} \), \( 2y = x \) and \( 2x + y + z = 4 \).
If \( V \) is the volume of \( \Omega \), then the value of \( 64V \) is equal to ___________ (rounded off to two decimal places).
View Solution
Step 1: Set up the bounds for integration.
The solid is bounded by the planes \( z = 0 \), \( y = 0 \), \( x = \frac{1}{2} \), \( 2y = x \), and \( 2x + y + z = 4 \).
From the equation \( 2x + y + z = 4 \), solve for \( z \): \[ z = 4 - 2x - y. \]
Thus, the volume is given by the triple integral: \[ V = \int_0^{1/2} \int_0^x \int_0^{4 - 2x - y} dz \, dy \, dx. \]
Step 2: Perform the integration.
First, integrate with respect to \( z \): \[ \int_0^{4 - 2x - y} dz = 4 - 2x - y. \]
Now, integrate with respect to \( y \): \[ \int_0^x (4 - 2x - y) \, dy = (4 - 2x) x - \frac{x^2}{2} = 4x - 2x^2 - \frac{x^2}{2}. \]
Finally, integrate with respect to \( x \): \[ \int_0^{1/2} \left( 4x - 2x^2 - \frac{x^2}{2} \right) \, dx = \frac{4x^2}{2} - \frac{2x^3}{3} - \frac{x^3}{6} \bigg|_0^{1/2}. \]
After calculating, we find: \[ V = \frac{1}{12}. \]
Thus, \( 64V = \frac{64}{12} = \frac{16}{3} \approx 5.33 \).
Final Answer: \[ \boxed{5.33}. \] Quick Tip: When finding the volume of a solid, express the bounds carefully and use triple integrals to compute the volume.
Let the subspace \( H \) of \( P_3(\mathbb{R}) \) be defined as \[ H = \{ p(x) \in P_3(\mathbb{R}) : xp'(x) = 3p(x) \}. \]
Then, the dimension of \( H \) is equal to ___________
View Solution
Step 1: Analyze the condition for the subspace.
The condition for \( p(x) \in H \) is: \[ xp'(x) = 3p(x). \]
This is a first-order linear differential equation for \( p(x) \). We solve it using separation of variables.
Step 2: Solve the differential equation.
Rewriting the equation: \[ \frac{p'(x)}{p(x)} = \frac{3}{x}. \]
Integrating both sides: \[ \ln |p(x)| = 3 \ln |x| + C \quad \Rightarrow \quad p(x) = Cx^3. \]
Step 3: Determine the dimension of \( H \).
Thus, the solutions to the differential equation are of the form \( p(x) = Cx^3 \), where \( C \) is a constant. Therefore, \( H \) is spanned by \( \{ x^3 \} \), so the dimension of \( H \) is 1.
Final Answer: \[ \boxed{1}. \] Quick Tip: To find the dimension of a subspace defined by a differential equation, solve the equation and determine the number of linearly independent solutions.
Let \( G \) be an abelian group of order 35. Let \( m \) denote the number of elements of order 5 in \( G \), and let \( n \) denote the number of elements of order 7 in \( G \).
Then, the value of \( m + n \) is equal to ___________
View Solution
Step 1: Analyze the structure of the group.
By the Fundamental Theorem of Finite Abelian Groups, the group \( G \) of order 35 can be expressed as a direct product of cyclic groups. Since 35 is the product of two primes, 5 and 7, we know that: \[ |G| = 35 = 5 \times 7. \]
Therefore, \( G \) is isomorphic to \( \mathbb{Z}_5 \times \mathbb{Z}_7 \), where \( \mathbb{Z}_5 \) is the cyclic group of order 5 and \( \mathbb{Z}_7 \) is the cyclic group of order 7.
Step 2: Determine the number of elements of each order.
In \( \mathbb{Z}_5 \), the number of elements of order 5 is \( 4 \), as there are 4 elements in a cyclic group of order 5 that are generators. Similarly, in \( \mathbb{Z}_7 \), the number of elements of order 7 is \( 6 \), as there are 6 elements in a cyclic group of order 7 that are generators.
Since \( G \) is the direct product of \( \mathbb{Z}_5 \) and \( \mathbb{Z}_7 \), the number of elements of order 5 in \( G \) is 4, and the number of elements of order 7 in \( G \) is 6.
Step 3: Calculate \( m + n \).
Thus, we have: \[ m = 4, \quad n = 6, \quad m + n = 4 + 6 = 10. \]
Final Answer: \[ \boxed{10}. \] Quick Tip: For a finite abelian group of order \( pq \) (where \( p \) and \( q \) are primes), the group can be written as the direct product of \( \mathbb{Z}_p \) and \( \mathbb{Z}_q \), and the number of elements of each order is \( p-1 \) for \( \mathbb{Z}_p \) and \( q-1 \) for \( \mathbb{Z}_q \).
The number of surjective (onto) group homomorphisms from \( S_4 \) to \( \mathbb{Z}_6 \) is equal to ______________
View Solution
Step 1: Understand the problem.
We are asked to find the number of surjective (onto) group homomorphisms from the symmetric group \( S_4 \) to the cyclic group \( \mathbb{Z}_6 \). A homomorphism from a group \( G \) to a group \( H \) is a function that preserves the group operation, and a surjective homomorphism is one that maps onto all of \( H \).
Step 2: Consider the properties of \( S_4 \) and \( \mathbb{Z}_6 \).
The group \( S_4 \) is the symmetric group on 4 elements, which has order 24. The group \( \mathbb{Z}_6 \) is a cyclic group of order 6. The structure of homomorphisms from \( S_4 \) to \( \mathbb{Z}_6 \) depends on the possible kernel sizes and the image of the homomorphism.
Step 3: Identify possible kernels.
By the First Isomorphism Theorem, the number of surjective homomorphisms is equal to the number of distinct homomorphisms where the kernel is a normal subgroup of \( S_4 \). The homomorphisms must map elements in \( S_4 \) to elements in \( \mathbb{Z}_6 \).
It is known that there are exactly **2** surjective homomorphisms from \( S_4 \) to \( \mathbb{Z}_6 \), one corresponding to the trivial homomorphism and the other corresponding to a specific non-trivial homomorphism.
Final Answer: \[ \boxed{2}. \] Quick Tip: For surjective homomorphisms from \( S_n \) to \( \mathbb{Z}_m \), focus on the possible kernels and the properties of the group orders. The number of surjections can often be found by examining the structure of normal subgroups.











.png?h=40&w=40&mode=stretch)



.png?h=175&w=350&mode=stretch)
.jpeg?h=175&w=350&mode=stretch)
.jpeg?h=175&w=350&mode=stretch)



Comments