
Jasmine Grover Content Strategy Manager
Content Strategy Manager | Updated On - Mar 17, 2025
Electric Current is defined as the amount of rate of flow of charges through any cross-section of a wire. The formula for electric current (I) is (q/t), where q is charge and t is the time of flow of charges. The SI unit used for electric current is Ampere (A). There are two types of electric current i.e, Direct and Alternating Current. The relationship between electric current and the potential difference can be said to Ohm’s Law. The formula of Ohm’s Law is V = IR, where R is the electrical resistance of the conductor.
Related Links
- Appearing for JEE Main, Download JEE Mains PYQ for all sabjects
- Appearing for NEET, Download NEET PYQ for all subjects
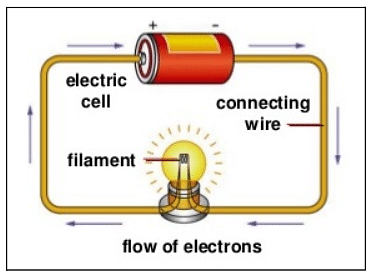
Current Electricity
Discover about the Chapter video:
Current Electricity Detailed Video Explanation:
Very Short Answer Questions (1 Mark Questions)
Ques. Two identical cells, each of emf E, the cells are given, have negligible internal resistance, which is connected in parallel with each other across an external resistance R. Find the current through this resistance? (CBSE AI 2013)
Ans. The current through this resistance can be written as I= E/R
Ques. A cell has emf E and internal resistance r which is connected across an external resistance R. Draw a graph showing the variation of P.D. across R, versus R. (NCERT)
Ans. The graph is given below shows emf E, resistance r and external resistance R.

Ques. State applications of Ohm’s Law.
Ans. Ohm’s Law is used to determine voltage, resistance or current.it is also used to maintain the voltage drop across the electric current. It is also used in an ammeter to divert the current.
Ques. Define the term Resistivity.
Ans. Resistivity is defined as the unit length of resistance and also the unit area of the conductor. It is also said to be specific resistance. It is different for every specific component.
Ques. When the circuit is set to close and a steady current passes through then explain is there a net field inside the cell?
Ans. The current flows in the electrostatic field direction from the outside and also the direction of the electrostatic field inside the cell is opposite when the circuit is set to be closed from the outside. So, there is a net field inside the Read More: which is opposite to the electrostatic field.
Ques. How does the relaxation time of electrons in the conductor change when the temperature of a good conductor decreases?
Ans. We know,
ρ = \(\frac{m}{ne^2T}\)
As the temperature of good conductor decreases, then the collision also decreases and thus the relaxation time of electrons also increases, where the resistivity decreases.
Ques. Write the relation between the terminal voltage V in form of E, I and r, where E is the emf of the cell and r is internal resistance.
Ans. The relation can be written as
V= E – I
Ques. What is Potentiometer?
Ans. A potentiometer is a device used for measuring the potential difference between the two points.
Ques. Explain the term ‘Mobility’ and its S.I unit
Ans. Mobility is termed as the magnitude of drift velocity per unit of the particular electric field in a conductor. The S.I unit is m2 V-1s-1.
Ques. When a potential difference is applied across the ends of a conductor, how is the drift velocity of the electrons related to the relaxation time?
Ans. We know that the drift velocity is directly proportional to relaxation time
Vd = \(\frac{eE}{m}τ\)
Ques. Two wires have equal length, one is made of copper and the other of manganin and they have the same resistance. Which wire here will be thicker between these two given wires?
Ans. Manganin wire will be thicker than copper wire.
Read More: Magnetic Field in A Solenoid Formula & Solved Examples
Short Answer Questions (2 Marks Questions)
Ques. When determining the emf of a cell, the potentiometer is preferred over the voltmeter. Why?
Ans. The potentiometer is referring as the null method or the cell does not produce any current and it measures emf. Hence, the voltmeter produces some current from the cell when it is connected across and measures terminal voltage.
Ques. A galvanometer coil has a resistance of 15Ω and gives full-scale deflection for a current of 4 mA. Convert it to an ammeter of range 0 to 6 A.
Ans. G = 15Ω, Ig = 4 mA, I = 6 A Required shunt will be,
S=\(\frac{I_{gG}}{I-I_g}\)
= \(\frac{4×10^{-3} ×15}{6-4×10^{-3}}\)
= \(\frac{6 ×10^{-2}}{6-0.004}= \frac{0.06}{5.996}\)
= 0.01Ω =10 mΩ
S = 10 mΩ
Ques. A 10 V battery which has a resistance of 38 and has negligible internal resistance is connected across a 200 V? as shown in the figure below. Determine the value of the current in the circuit. (Delhi 2013)
Ans.

Using the Kirchhoff’s rule, we can find
Equivalent emf of batteries =200 - 10= 190 V
Then, I =V/R
= 100/38 = 5 A
Ques. When electrons drift in metal from lower to higher potential, does it mean that all the free electrons of the metal are moving in the same direction? (Delhi 2012)
Ans.

No, only the drift velocities of the electrons are superimposed over their thermal (haphazard) velocities where all the electrons will not move in the same direction. The solid line given in the figure denotes a path followed by a free electron in the lack of an electric field.
Ques. When the circuit is set to close and a steady current passes through then explain is there a net field inside the cell?
Ans. The current flows in the electrostatic field direction from the outside and also the direction of the electrostatic field inside the cell is opposite when the circuit is set to be closed from the outside. So, there is a net field inside the cell which is opposite to the electrostatic field.
Ques. Two electric bulbs P and Q have their resistances in the ratio of 1: 2. They are connected in series across a battery. Calculate what will be the ratio of the power dissipation in these bulbs. (CBSE AI, Delhi 2018)
Ans. P = I2 R => P ∝ R => \(\frac{P_1}{P_2} = \frac{R_1}{R_2}\)
Now for two Bulbs P and Q, we have \(\frac{P_1}{P_2} = \frac{R_1}{R_2} = \frac{1}{2}\)
(since R1 : R2 = 1 : 2 given)
- Ratio of Power P1 : P2 = 1: 2
Ques. Find the potential difference across the whole terminals for given cell which has an emf of 5.0 volt and also an internal resistance of 1.0 volt. Cell terminals are joined through a 9 Ω resistor.
Ans. We know that,
V= E- Ir
E/R+r = 5/9+1A = 1/2A
So, V=E-Ir
= 5-1/2*1
Hence, V = 4.5 volt
Ques. A battery that contains emf E and internal resistance r when connected across an external resistance of 12 ft, produces a current of 0.5 A. When connected across a resistance of a distance of 25 ft, it produces a current of 0.25 A. Find the following.
(i) the emf
(ii) the internal resistance of the cell.
Ans. I = \(\frac{E}{R + r}\) \(\frac{E}{12 + r} = 0.5\) ….(i)
and \(\frac{E}{25+r} = 0.25 \) …..(ii)
Comparing (i) and (ii), we get
\(\frac{\frac{E}{12+r}}{\frac{E}{25+r}} = \frac{0.5}{0.25}\) ⇒\(\frac{25+r}{12+r} = \frac{0.5}{0.25}\) = 2
Solving we get, r = 1Ω
∴ E = 0.5(12+1) ⇒ E = 0.5 x 13 = 6.5 V
Also Read:
Long Answer Questions (3 Marks Questions)
Ques. The current in the below-given circuit is 0.2 A and calculate the value of resistance R. Also find the potential difference between points A and B.

Ans.

Across BE equivalent resistance R2
\(\frac{1}{R_2} = \frac{1}{10} + \frac{1}{30} + \frac{1}{15} \)= \(\frac{3+1+2}{30}\) = \(\frac{6}{30} = \frac{1}{5}\)
- R2 = 5
Potential difference VBE= I × R2 = 0.2 × 5
- VBE= 1V
Ques. Using the following figure find the current through each resistor.

Ans. E2 - E1 = 8 – 4 = 4 volt
Total resistance = 0.5 + 1 + 4.5 + \(\frac{6 \times 3}{6+3}\)=8
I=\(\frac{4}{8}\)=0.5 A
Current through 3 resistor
= \(\frac{6 \times 3}{6+3}\) = 0.33 A
Current through 3 resistor
= \(\frac{3 \times 0.5}{6+3}\) = 0.16 A
Ques. The resistance of the platinum wire of a platinum resistance thermometer at the ice point is 5 Ω and at steam, the point is 5.23 Ω. When the thermometer has been inserted into a hot bath, the resistance of the platinum wire is 5.795 Ω. Calculate the temperature of the bath as per the resistance given. (NCERT)
Ans. Given that, R0 = 5 Ω, R100 = 5.23 Ω, Rt = 5.795 Ω
NOW t= \(\frac{R_1-R_o}{R_{100}-R_o}\) × 100
Or t= \(\frac{5.795-5}{5.23-5}\) × 100 = 345.65°C
Ques. A battery of emf 10 V and internal resistance 3Ω has been connected to a resistor. If the current in the circuit is given 0.5 A, then find
(I) the resistance of the resistor;
(ii) the terminal voltage of the battery.
Ans. As given,
E = 10 V , r = 3 Ω, I = 0.5 A, R=? , V=?
- I = \(\frac{E}{R+r}\)
R + r = \(\frac{E}{I}\)= \(\frac{10}{0.5}\)=20
Or R = 20 – r
R = 20 – 3 = 17 Ω
- V = IR = 0.5 × 17 = 8.5 V
Ques. The average drift speed of conduction electrons in a copper wire of cross-sectional area is 1.0 × 10 -7 m2 carrying a current of 1.5 A. Assume that the density of conduction electrons is 9 × 1028 m-3. (All India 2014)
Ans. Given :
Current I=1.5 A, Cross-sectional area A = 1×10-7 m2
We know that,
I= neAVd
So, Drift Velocity Vd = \(\frac{I}{neA}\)
⇒ Vd = \(\frac{1.5}{9*10^{28}*(1.6*10^{-19})*(1.0*10^{-7})}\)1
Vd = 10.4 x 10 -4 m/s
Ques. Explain Ohm’s Law.
Ans. This Ohm’s Law states that the current that flows through a conductor is directly proportional to its potential difference applied across its ends, here the temperature and physical conditions remain unchanged. Here the current is directly proportional to voltage through a resistor, which means the current doubles then the voltage also doubles. To make current flow there should be a voltage across that resistance. Ohm’s Law states the relationship between these terms: voltage V, current I and resistance R. This can be written as:
V α I or I α V
V= IR
Where R resistance is constant. The value of it depends upon the nature, cross-section, length and temperature conductor. Here, V = potential difference is in Volt, I= current is in Ampere and R= resistance (constant). The SI unit of resistance is Ohm and denoted by Omega (Ω). The necessary condition of Ohm’s Law for applications like
- To find out the voltage, resistance or current of an electric circuit.
- It is also used to find the desired voltage drop across the electric components.
- It is also used in devices like dc ammeter and other dc shunts to divert the current.
For Ohm’s Law, it is important that the temperature should be constant. It is right only for electric elements. For elements like capacitance, resistance, etc. the voltage and current will not be constant with respect to time. Ohm’s Law is also not applicable for unilateral elements like diodes and transistors because here current flows in one direction only.
Ques. Explain Wheatstone Bridge.
Ans.

The Wheatstone Bridge is an arrangement made up of four resistances connected with each other to form the arms of shape like a quadrilateral A battery with key and galvanometer are connected at its two diagonals positions. Where R1 and R3 are standard arms or ratio arms, R2 is known resistance and R4 is unknown resistance. The bridge is balanced when
- Vb=Vd
- Here, there is no flow of current through the galvanometer.
The Wheatstone bridge is known to be sensitive because there will be a slight change of resistance in the galvanometer due to ample deflection. For the sensitivity of any galvanometer, the magnitude of all four resistances should be in the same order as A, B, C, and D
Read More: Converting a Galvanometer Into a Voltmeter of Desired Range
Very Long Answer Questions (5 Marks Questions)
Ques. (i) State the principle of working of a meter bridge.
(ii) In a meter bridge balance point is found at a distance l1 with resistances R and S as shown in the figure. The balance point shifts to a distance l2 when an unknown resistance X is connected in parallel with the resistance S. Calculate what will be the expression for X in terms of l1 l2 and S. (All India 2009)

Ans. (i) Meter bridge: Meter bridge is an arrangement made up of four resistances used for measurement between one unknown resistance in terms of the other three known resistances.

(ii) With R and S alone, we get that
\(\frac{R}{S} = \frac{I_1}{(100 - I_1)} ....(i) \) ⇒ R(100 – I1) = S1here S and X are in parallel and R on the left gap
\(\frac{R}{(\frac{SX}{S+X})} = \frac{I_2}{(100 - I_2)}\)
⇒ \(\frac{R(S+X)}{SX} = \frac{I_2}{100 - I_2}\) …...(ii)
Dividing (ii) by (i), we have
\(\frac{R(S+X)}{SX}. \frac{S}{R} = \frac{I_2}{100 - I_2} \times \frac{100-I_1}{I_1}\)
⇒ \(\frac{S+X}{X} = \frac{I_2(100 - I_1)}{I_1(100-I_2)}\)
⇒ \(\frac{S}{X} + \frac{X}{X} = \frac{I_2(100 - I_1)}{I_1(100-I_2)}\)
⇒ \(\frac{S}{X} + 1 = \frac{I_2(100 - I_1)}{I_1(100-I_2)}\)
⇒ \(\frac{S}{X}= \frac{I_2(100 - I_1)}{I_1(100-I_2)} - 1\)
⇒ \(\frac{S}{X}= \frac{100I_2 - I_1I_2 - 100I_1 + I_1I_2}{I_1(100-I_2)}\)
⇒ \(\frac{S}{X}= \frac{100(I_2 - I_1)}{I_1(100-I_2)}\) ⇒ X = \( \frac{I_1(100-I_2)}{100(I_2 - I_1)}\).S
∴ X = \(\frac{100I_1S - I_1I_2S}{100(I_2 - I_1)}\)
Ques. Using Kirchhoff’s rules determine the value of unknown resistance R into the circuit so that no current flows through 4ω resistance. Also, find the potential difference between A and D. (Delhi 2012)

Ans. Applying Kirchhoff’s Voltage rule for loop ABEFA
-9 + 6 + 4 * 0 + 2I = 0
=> 2I – 3 = 0
=> I = 3/2 A = 1.5 A … (1)
For loop BCDEB
3 + IR + 4 * 0 – 6 = 0
∴ IR = 3
Putting the value of current I from (1), we have
\(\frac{3}{2}\) × R = 3
∴ R = 3 x \(\frac{2}{3}\) = VAD
(Alternatively, through path AFD)
∴ VAD =3 V
Ques. A galvanometer of resistance G is converted into a voltmeter to measure up to V volts by connecting a resistance Rx in series with the coil. If a resistance R2 is connected in series connection with it, then it can measure up to V/2 volts. Measure the resistance, in terms of resistance as R1 and R2, required to be connected to convert it into a voltmeter that can read up to 2V. Also, find the resistance G of the galvanometer in terms of R1 and R2. (Delhi 2012)
Ans. (a) principle used for working of galvanometer
When a coil carrying current experiences a torque when it is placed in a magnetic field which makes the coil to rotate and it produces an angular deflection.
(b) V = I (G + R1) … (1)
\(\frac{V}{2} \)= I (G + R2) … (2)
Dividing (1) by (2), we have
- 2 = \(\frac{G+ R_1}{G+R_2}\)
- G = R1 - 2R2
Let R3 be the resistance required for
conversion into voltmeter of range 2V
∴ 2V = Ig (G + R3) … (3)
Also, V = Ig (G + R3) … (4)
Dividing (3) by (4), we get
∴ 2 = \(\frac{G+ R_3}{G+R_1}\)
∴ R3 = G + 2R1 = (R1 – 2R2) + 2R1
= 3R1 – 2R2 ... (From value of G)
Ques. Explain the two Kirchhoff’s Laws. And also justify these laws.
Ans. There are two Kirchhoff’s laws and they are Kirchhoff’s current law and Kirchhoff’s voltage law.
Kirchhoff’s current law: Kirchhoff’s junction rule is also said to be Kirchhoff’s point rule, it is the algebraic sum of currents of conductors which are in a network and meeting at a point is zero. Basically, the sum of currents entering the junction is equal to the sum of leaving currents at that junction.

- As per figure A, the sum will be i1 + i2 = i3.
- As per figure B, the sum will be i1 = i2 + i3 + i4.
- As per figure C, the sum will be i1 + i2 + i3 = 0.
In the last given figure, we can observe that the current flow in and doesn’t go out. Here the directions for every current problem are solved arbitrarily. So here the problem is solved, some currents have negative value, which shows that the actual current will flow in opposite direction as compared with arbitrarily chosen initially. If the current value is positive then the direction of the current is the same as chosen initially.
Kirchhoff’s voltage law is also said as Kirchhoff’s loop rule. Here the law states that the sum of electromotive forces in a loop is equal to the sum of potential drops in the loop. It can also be said as the directed sum of voltages is zero around every closed loop. It can be known from the below-given figure.
Here the potential difference can be written as, Vb - Va = E1. As per the figure.

As same for the potential difference Vc - Vd is written as -E2. i,e; Vc - Vd = -E2. Using Ohm’s Law, Vb - Vc = iR1, and Vd - Va = iR2. These four relations of equations make loop equation as E1 - E2 - iR1 - iR2 = 0. Here, R1 and R2 are values of resistances in ohms and EMF (electromotive forces) as E1 and E2 in volts, the current value I is obtained here. If E2 > E1 then the current will be negative and it indicates the current flows in opposite direction. This law can be understood from the following figure as well.

Ques. Find the value of current I1 which is flowing in the circuit given below. Find the value by using Kirchhoff’s rules.

Ans. By Kirchhoff’s first law at junction E, we get current
I3 = I3 + I2
By Kirchhoff’s second law in the loop ABCDA

- - 20 I2 + 30 I1 = 0
- 2I2 – 3I1 = 8 [ by 10] ... (1)
In loop ABFEA, we get
80 - 20I2 +20 - 20I3 =0
- I2 – I3 = 5 [ by 20] ... (2)
Putting the value of I3 into (2), we have
I2 + (I2 + I2 )=5 => 2 I2 + I1 =5 … (3)
Solving equations (2) and (3), we get
I1 = -\(\frac{3}{4}\)A = – 0.75 A
Here the current value obtained is negative means the direction is opposite as per the figure given above.
For Latest Updates on Upcoming Board Exams, Click Here: https://t.me/class_10_12_board_updates
Check-Out:





Comments