.jpg?h=55&w=55&mode=stretch)
Content Curator
KEAM 2012 Physics and Chemistry Question Paper with Answer Key pdf is available for download. The exam was conducted by Commissioner of Entrance Examination (CEE) on April 23, 2012 in the Morning Session 10 AM to 12:30 PM. The question paper comprised a total of 120 questions divided among 2 sections.
KEAM 2012 Physics and Chemistry Question Paper with Answer Key PDF
| KEAM 2012 Physics and Chemistry Question Paper PDF | KEAM 2012 Physics and Chemistry Answer Key PDF |
|---|---|
| Download PDF | Download PDF |
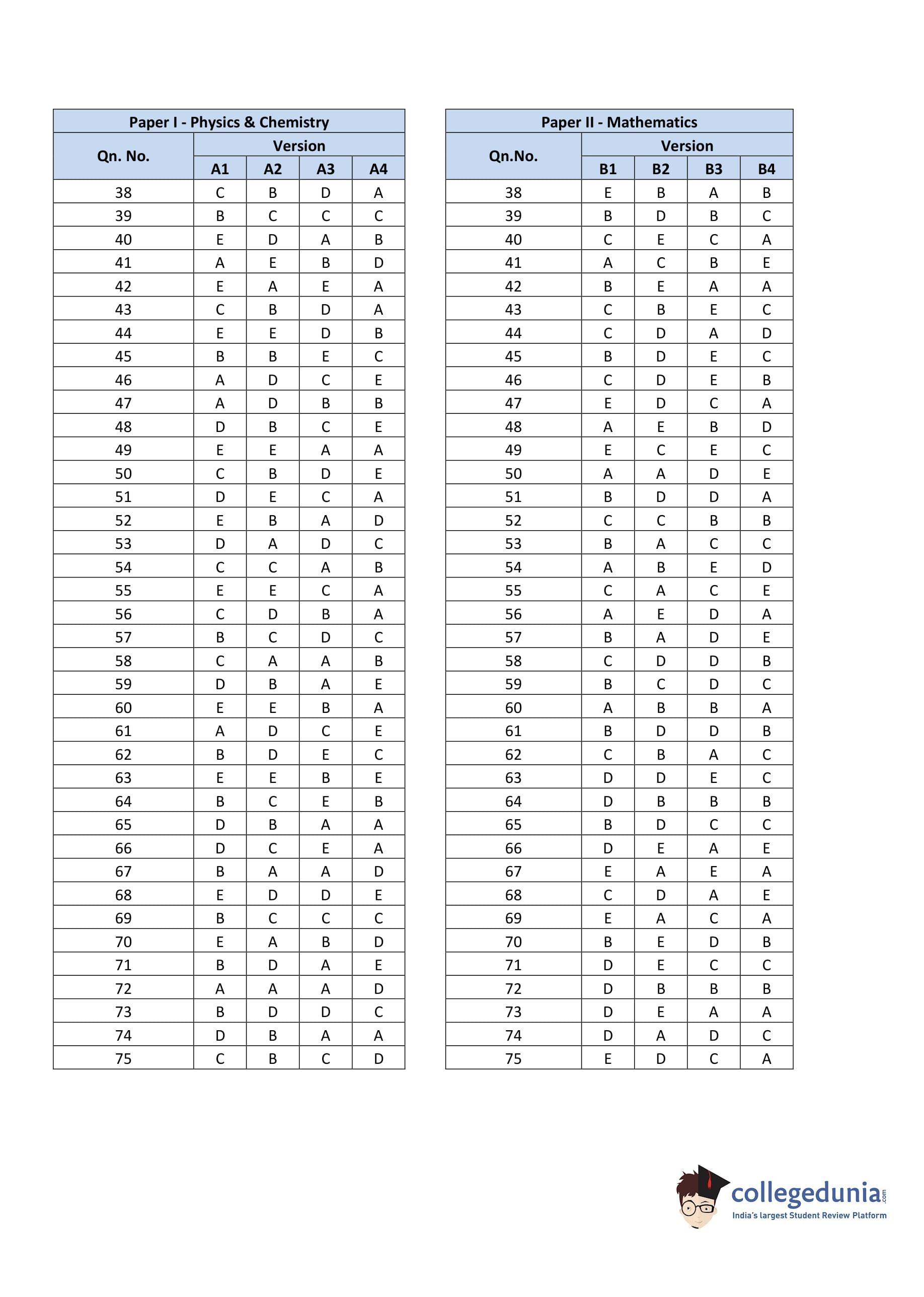
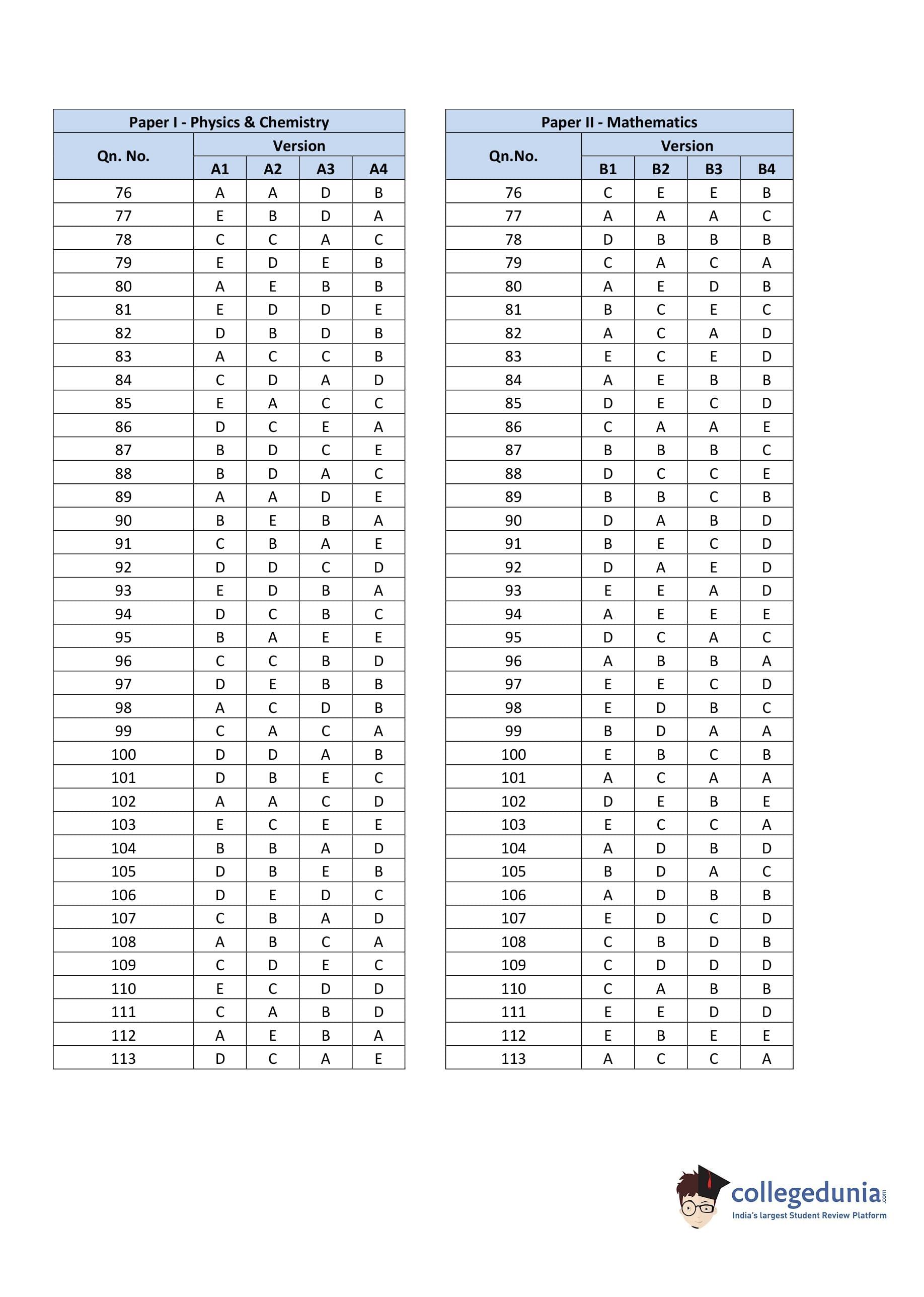
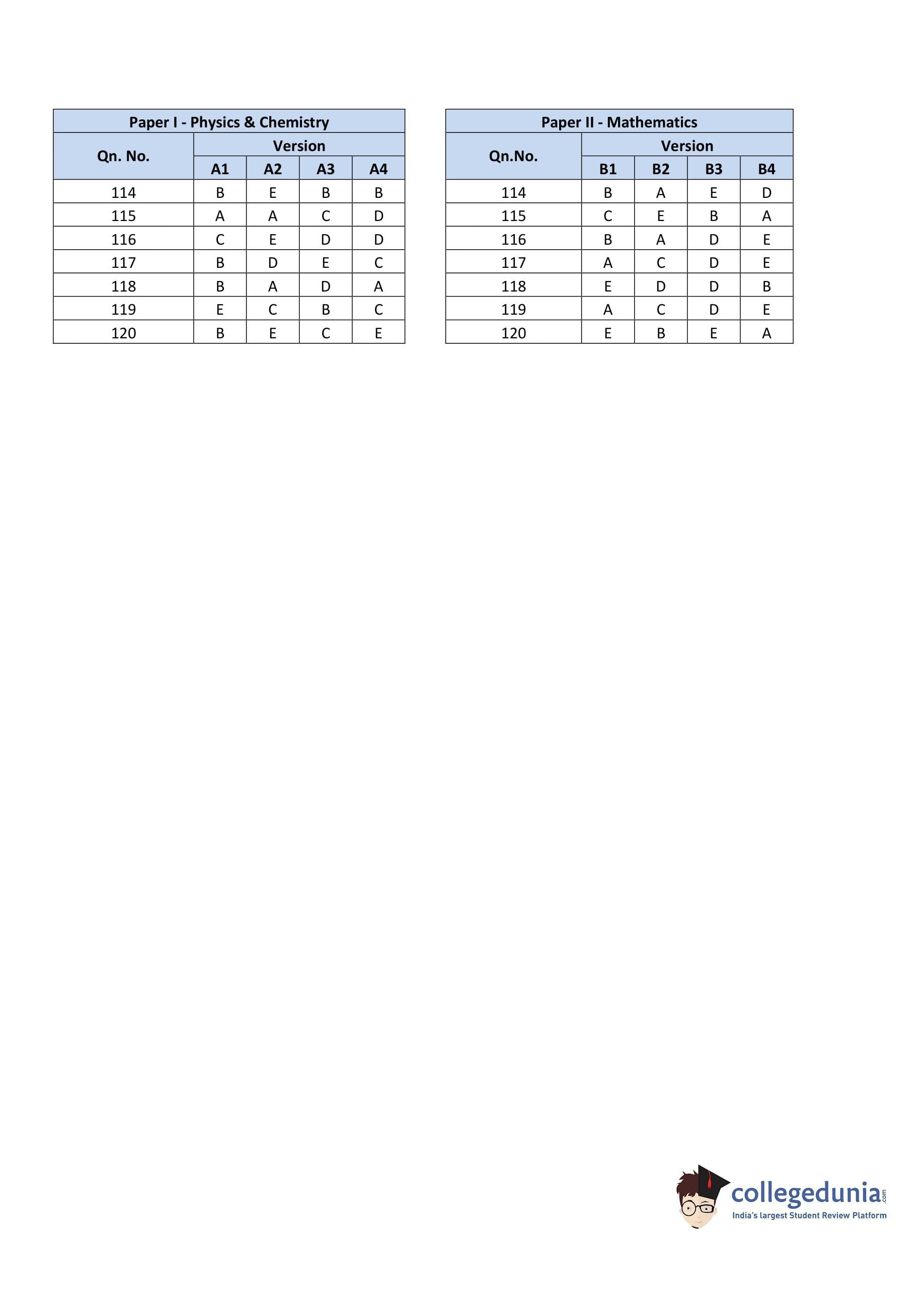
KEAM Previous Year Question Paper with Answer Key PDFs
| KEAM 2021 Question Papers | KEAM 2020 Question Papers | KEAM 2019 Question Papers |
| KEAM 2018 Question Papers | KEAM 2017 Question Papers | KEAM Practice Papers |
Similar Exam Question Papers
KEAM Questions
1. The angle of minimum deviation for a prism of apex angle 60° and refractive index of \(\sqrt{2}\) is:
The angle of minimum deviation for a prism of apex angle 60° and refractive index of \(\sqrt{2}\) is:
45°
90°
30°
60°
15°
2. Let α and β be such that α+β=π. If \(\cos\alpha=\frac{1}{\sqrt2}\), then the value of cot (β-α) is
Let α and β be such that α+β=π. If \(\cos\alpha=\frac{1}{\sqrt2}\), then the value of cot (β-α) is
- ∞
- 1
- \(\frac{1}{2}\)
- \(\frac{1}{4}\)
- 0
3. In a Zener regulated power supply circuit as shown in figure below,a Zener diode with Vz=1OV is used for regulation. The load current,Zener current and unregulated input Vin are 5mA,35mA and 20V,respectively. The value of R is:
In a Zener regulated power supply circuit as shown in figure below,a Zener diode with Vz=1OV is used for regulation. The load current,Zener current and unregulated input Vin are 5mA,35mA and 20V,respectively. The value of R is:
1000Ω
750Ω
250Ω
100Ω
500Ω
4. If the coefficients of \((5r+4)th\) term and \((r-1)th\) term in the expansion of \((1+x)^{25}\) are equal, then \(r\) is
If the coefficients of \((5r+4)th\) term and \((r-1)th\) term in the expansion of \((1+x)^{25}\) are equal, then \(r\) is
\(6\)
\(3\)
\(5\)3
\(2\)
\(4\)
5. Suppose \(A=\begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{bmatrix}\) is an adjoint of the matrix \(\begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4\end{bmatrix}\). Then the value of \(\frac{a_!+b_2+c_3}{b_1a_2}\) is
Suppose \(A=\begin{bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3\end{bmatrix}\) is an adjoint of the matrix \(\begin{bmatrix} 1 & 3 & 3 \\ 1 & 4 & 3 \\ 1 & 3 & 4\end{bmatrix}\). Then the value of \(\frac{a_!+b_2+c_3}{b_1a_2}\) is
- 0
- 3
- 1
- 2
- 4
6. If \(x\) is a real number such that \(tanx+cotx=2\),then \(x=\)?
If \(x\) is a real number such that \(tanx+cotx=2\),then \(x=\)?
\( (n+\dfrac{1}{4})π,n∈Z\)
\((n+1)π,n∈Z\)
\( (n+\dfrac{1}{2})π,n∈Z\)
\(nπ,n∈Z\)
\( \dfrac{2}{3}nπ,n∈Z\)
.jpeg?h=160&w=320&mode=stretch)
.png?h=160&w=320&mode=stretch)
.png?h=160&w=320&mode=stretch)
Comments