\(\lim_{x\rightarrow \infty}\){\(x-\sqrt[n]{(x-a_1)(x-a_2)......(x-a_n)}\)} where a1,a2,.....an are positive rational numbers.The limit
- does not exist
is \(\frac{a_1+a_2+....+a_n}{n}\)
- is \(\sqrt[n]{a_1a_2.....a_n}\)
- is \(\frac{n}{a_1+a_2+....+a_n}\)
The Correct Option is B
Approach Solution - 1
The correct option is(B): \(\frac{a_1+a_2+....+a_n}{n}\)
Approach Solution -2
Given:
\(\lim_{x \rightarrow \infty} \left( x - \sqrt[x]{(x-a_1)(x-a_2) \ldots (x-a_n)} \right)\)
As x becomes very large, each \(x - a_i\) where \(a_i\) are constants becomes negligible compared to x. Therefore, we can approximate:
\(\sqrt[x]{(x-a_1)(x-a_2) \ldots (x-a_n)} \approx \sqrt[x]{x^n \left( 1 - \frac{a_1}{x} \right)\left( 1 - \frac{a_2}{x} \right) \ldots \left( 1 - \frac{a_n}{x} \right)}\)
\(\approx x \left[ 1 - \left( 1 - \frac{a_1}{x} \right)^{1/n} \left( 1 - \frac{a_2}{x} \right)^{1/n} \ldots \left( 1 - \frac{a_n}{x} \right)^{1/n} \right]\)
\(\approx x \left[ 1 - \left( 1 - \frac{a_1}{nx} \right)\left( 1 - \frac{a_2}{nx} \right) \ldots \left( 1 - \frac{a_n}{nx} \right) \right]\)
\(\approx x \left[ \frac{a_1 + a_2 + \ldots + a_n}{nx} \right]\)
\(= \frac{a_1 + a_2 + \ldots + a_n}{n}\)
So, the correct option (B): \(\frac{a_1 + a_2 + \ldots + a_n}{n}\).
Top Questions on Limits
- If \(lim_{x\rightarrow 0} \frac{\sqrt 1 + \sqrt{1+x^4}-\sqrt 2}{x^4}=A\) and \(lim_{x \rightarrow 0} \frac{sin^2x}{\sqrt 2 - \sqrt{1+cosx}}=B\), then \(AB^3\) = ____.
- $ \lim_{𝑥→\infty}(1+\frac{1}{x})$ is equal to
- Let \(k\in R\). If \(\)\(\)\(\)\(\lim\limits_{x→0+}(\sin(\sin kx)+\cos x+x)^{\frac{2}{x}}=e^6\), then the value of k is
- Let S be the set of all \((α, β) ∈ \R\times\R\) such that
\(\lim\limits_{x\rightarrow\infin}\frac{\sin(x^2)(\log_ex)^\alpha\sin(\frac{1}{x^2})}{x^{αβ}(\log_e(1+x))^β}=0\)
Then which of the following is (are) correct ? - \(\lim\limits_{x→0} \frac {e^{|2sinx|}-2|sinx|-1}{x^2}\) is
Questions Asked in WBJEE exam
- In an experiment on a circuit, as shown in the figure, the voltmeter shows 8V reading. The resistance of the voltmeter is
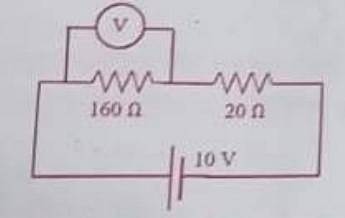
- WBJEE - 2023
- Resistance
- The value of 'a' for which the scaler triple product formed by the vectors \(\vec\alpha=\hat{i}+a\hat{j}+\hat{k}\), \(\vec{\beta}=\hat{j}+a\hat{k}\) and \(\vec{\gamma}=a\hat{i}+\hat{k}\) is maximum, is
- WBJEE - 2023
- Vector Algebra
- A rectangle ABCD has its side parallel to the line y=2x and vertices A,B,D are on y=1,x=1 and x=-1 respectively. The coordinate of C can be
- WBJEE - 2023
- Straight lines
- A missile is fired from the ground level rises x meters vertically upwards in t sec, where \(x=100t-\frac{25}{2}t^2\). the maximum height reached is
- WBJEE - 2023
- Differential equations
The equivalent weight of KIO3 in the given reaction is (M=molecular mass) :
2Cr(OH)3 + 4OH + KIO3 → 2CrO42- + 5H2O +KI- WBJEE - 2023
- Redox reactions
Concepts Used:
Limits
A function's limit is a number that a function reaches when its independent variable comes to a certain value. The value (say a) to which the function f(x) approaches casually as the independent variable x approaches casually a given value "A" denoted as f(x) = A.
If limx→a- f(x) is the expected value of f when x = a, given the values of ‘f’ near x to the left of ‘a’. This value is also called the left-hand limit of ‘f’ at a.
If limx→a+ f(x) is the expected value of f when x = a, given the values of ‘f’ near x to the right of ‘a’. This value is also called the right-hand limit of f(x) at a.
If the right-hand and left-hand limits concur, then it is referred to as a common value as the limit of f(x) at x = a and denote it by lim x→a f(x).



